臨床工学技士問題表示
臨床工学技士国家試験
解説
円管(まっすぐな血管)内のレイノルズ数は $\text{Re} = \frac{\rho v D}{\mu}$ で与えられる。ここで、密度 $\rho = 1\times10^3\,\text{kg}/\text{m}^3$、平均流速 $v = 0.2\,\text{m}/\text{s}$、直径 $D = 20\,\text{mm} = 0.020\,\text{m}$、粘性係数(動粘性率ではなく動粘度)$\mu = 0.004\,\text{Pa}\cdot\text{s}$ を代入すると、$\text{Re} = \frac{(1000)\times(0.2)\times(0.020)}{0.004} = \frac{4}{0.004} = 1000$ となる。一般に円管内では $\text{Re} \lesssim 2300$ が層流、$\text{Re} \gtrsim 4000$ が乱流とされ、本条件は層流域の値である。よって該当する選択肢は「1000」。
選択肢別解説
誤り。レイノルズ数は $\text{Re} = \frac{\rho v D}{\mu}$ により、$\rho=1000\,\text{kg}/\text{m}^3$、$v=0.2\,\text{m}/\text{s}$、$D=0.020\,\text{m}$、$\mu=0.004\,\text{Pa}\cdot\text{s}$ を代入すると 1000 となる。1 にはならない。
誤り。数値を代入して計算すると $\text{Re}=1000$ であり、20 ではない。
誤り。計算は $\text{Re} = \frac{(1000)(0.2)(0.020)}{0.004} = 1000$ となるため、500 ではない。
正しい。$\text{Re} = \frac{\rho v D}{\mu}$ により、$\rho=1000\,\text{kg}/\text{m}^3$、$v=0.2\,\text{m}/\text{s}$、$D=0.020\,\text{m}$、$\mu=0.004\,\text{Pa}\cdot\text{s}$ を代入して $\text{Re}=1000$。
誤り。上記の通り計算結果は 1000 であり、5000 ではない。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
動圧は流体の運動エネルギーに由来する圧で、ベルヌーイの定理より $P_d=\tfrac{1}{2}\rho v^2$ で与えられる。血液の密度はおよそ $\rho=1{,}060\ \text{kg/m}^3$(近似として水の $1{,}000\ \text{kg/m}^3$ でも可)とし、流速 $v=1\ \text{m/s}$ を代入すると、$P_d\approx\tfrac{1}{2}\times1{,}000\times1^2=500\ \text{Pa}$(血液密度を用いると約 $530\ \text{Pa}$)。圧力換算は $1\ \text{mmHg}\approx133.3\ \text{Pa}$ を用いるため、$500/133.3\approx3.8\ \text{mmHg}$(血液密度なら $\approx4.0\ \text{mmHg}$)。したがっておよその値は 4 mmHg が妥当である。
選択肢別解説
0.4 mmHg は過小。$P_d=\tfrac{1}{2}\rho v^2$ に $\rho\approx1{,}000\ \text{kg/m}^3$, $v=1\ \text{m/s}$ を代入すると $\approx3.8\ \text{mmHg}$ となり、0.4 mmHg は約 1/10 と小さすぎる。
1 mmHg も過小。計算値は $\approx3.8\text{--}4.0\ \text{mmHg}$ であり、1 mmHg は約 1/4 と小さい。
4 mmHg は $P_d=\tfrac{1}{2}\rho v^2$ と $1\ \text{mmHg}\approx133.3\ \text{Pa}$ の換算から得られるおよその値(約 3.8~4.0 mmHg)と一致し、妥当。
10 mmHg は過大。$P_d=10\ \text{mmHg}$ になる速度は $v=\sqrt{2\,\Delta P/\rho}\approx\sqrt{2\times(10\times133.3)/1000}\approx1.63\ \text{m/s}$ で、$v=1\ \text{m/s}$ の条件には合致しない。
40 mmHg は著しく過大。$P_d=40\ \text{mmHg}$ 相当は $v\approx\sqrt{2\times(40\times133.3)/1000}\approx3.27\ \text{m/s}$ を要し、$v=1\ \text{m/s}$ の条件とは一致しない。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
流量制御型(容積制御方式)の輸液ポンプは、ローラ式ペリスタルティックやカセット式(ピストン・ダイヤフラム等)などの機構で、機械的に一定体積を押し出して流量を制御する。したがって重力や滴下の大きさに依存せず、輸液の粘性・表面張力・濃度といった“成分”による影響を受けにくく、滴数制御型より流量のばらつきは小さい。一方で、正確な容積送液にはチューブの材質・内径・弾性が規格化された専用セットを要することが多く、長時間の圧閉に伴うチューブのへたり(内径・弹性変化)が送液誤差の要因となる。
選択肢別解説
正しい。容積制御方式は1回転(あるいは1ストローク)当たりの押し出し体積で送液量を決めるため、滴下の大きさや重力に依存しない。よって輸液の粘性・表面張力・濃度など“成分”の違いによる流量誤差は基本的に生じにくい(指定粘度範囲内という前提)。
誤り。容積制御方式は所定の精度で体積を搬送するために、チューブの内径・硬さ・伸び特性が規定された専用の輸液セットを用いるのが原則であり、汎用セットでは精度が保証されない。
誤り。滴下センサは滴数制御型で必要となる。容積制御方式はポンプ機構そのもので送液量を制御するため滴下検出は不要である(代わりに気泡検出や閉塞検出などのセンサを備える)。
誤り。容積制御方式は体積基準で送液するため、滴数制御型に比べて流量のばらつきは小さい。滴数制御型は滴下サイズや点滴筒の姿勢、薬液性状の影響を受けやすい。
正しい。ローラ等でチューブを圧閉して送液する方式では、長時間使用でチューブがへたり弾性や内径が変化し、1回転あたりの実効搬送量が変動して流量誤差の原因となる。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
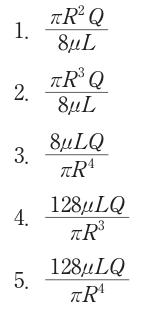
解説
層流の円管内流れではハーゲン・ポアズイユの法則が成り立ち、ニュートン流体・直円管・完全発達・定常の条件下で流量と圧力差の関係は $Q=\frac{\pi R^4}{8\mu L}\,\Delta P$ と表される。これを圧力差について解くと $\Delta P=\frac{8\mu L}{\pi R^4}Q$ となり、管半径には4乗で強く依存する(半径が半分になれば必要圧力差は16倍)。よって正答は選択肢3。係数128は直径 $D$ を用いた表式に対応するため、本問(半径表記)では不適切。
選択肢別解説
誤り。$\Delta P$ は $\frac{8\mu L}{\pi R^4}Q$ に等しいため、半径への依存は $R^{-4}$ である。本式は $R^2$ に比例しており依存性が逆かつ係数も不正。
誤り。ハーゲン・ポアズイユの法則では $\Delta P\propto Q\mu L/R^4$。本式は $R^3$ に比例しており、半径依存が誤っている。
正しい。ハーゲン・ポアズイユの法則 $Q=\frac{\pi R^4}{8\mu L}\Delta P$ を $\Delta P$ について解くと $\Delta P=\frac{8\mu L}{\pi R^4}Q$ となる。
誤り。分母が $R^3$ となっており次数が不正。さらに係数128は直径 $D$ を用いるときの式に由来し、半径表記では8となる。
誤り。半径 $R$ を用いる圧力差の係数は $\frac{8}{\pi}$ であり128ではない。128は $D$(直径)を用いた形での係数である。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
膜型人工肺では、均質膜(シリコーン)と多孔質膜(主としてポリプロピレン中空糸)が用いられる。シリコーン膜は気体溶解度の差によりCO₂透過性がO₂より高く、一般に約4~5倍とされる。一方、ポリプロピレン中空糸は機械的強度に優れ薄膜化が可能で、現在の主流である。多孔質膜は微細孔を介するため血液とガスが事実上直接接触し(プラズマリークや微小気泡の管理が課題)、均質膜では固体膜を隔てて拡散する。血液の灌流様式では、内部灌流型(血液が中空糸内を流れる)は層流になりやすく圧力損失は大きい。外部灌流型(中空糸外側を血液が流れる)は混合・乱流化しやすい反面、圧力損失は比較的小さい。以上より、設問の正誤は1・2が正しく、3・4・5は誤りとなる。
選択肢別解説
正しい。シリコーン膜は均質膜で、気体透過性は拡散係数と溶解度に依存する。CO₂はO₂より溶解度が高く、総合的な透過性はO₂の約4~5倍とされるため「CO₂の方が高い」は妥当。
正しい。シリコーン膜は機械的強度が低く薄膜化に限界がある。ポリプロピレン中空糸(多孔質膜)は機械的強度に優れ、薄くしても強度を保ち量産性も高いため、シリコーンより強度面で優れている。
誤り。多孔質膜(microporous)は微細孔を介して血液とガスが実質的に直接接触する(界面は孔内で形成)。そのためプラズマリークや微小気泡管理が課題となる。血液とガスが固体膜で完全に隔てられるのは均質膜(シリコーン)である。
誤り。内部灌流型は中空糸内という狭小・均一な流路を血液が通るため層流になりやすい。乱流化しやすいのは中空糸外の広い空間を血液が流れる外部灌流型である。
誤り。圧力損失は内部灌流型の方が大きい(中空糸内腔が狭い)。外部灌流型は比較的圧力損失が小さいため、記述は逆である。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。