臨床工学技士問題表示
臨床工学技士国家試験
解説
人工心肺の血液ポンプには主にローラポンプ(容積式)と遠心ポンプ(非容積式)がある。ローラポンプはチューブを機械的に圧閉して送液するため、停止時でも適切なオクルージョン設定で逆流は基本的に起こらない。一方で回路閉塞時は高圧が発生しやすく、溶血などの血液損傷も遠心ポンプより大きい。遠心ポンプは回転数だけでなく前負荷・後負荷により流量が変化する特性(圧流量特性)を持ち、後負荷(下流側圧)が高まると流量は減少する。また回路閉塞時に極端な高圧を生じにくい(圧が自己制限的)ため、回路破裂の危険はローラポンプより小さい。以上から、正しい記述は「遠心ポンプでは後負荷が高いほど流量が減少する」である。
選択肢別解説
誤り。ローラポンプはチューブを圧閉する容積式であり、適切なオクルージョン設定下では停止時の逆流は基本的に防止される。逆流が“生じやすい”とはいえない(安全対策としてクランプや逆止弁を併用することはある)。
誤り。ローラポンプはチューブをしごく機械的作用により血液にせん断・圧挫ストレスが加わり、遠心ポンプより溶血などの血液損傷が大きくなりやすい。
誤り。遠心ポンプは自己制限的な圧特性を持ち、回路閉塞時には流量が低下して高圧が生じにくい。高圧による回路破裂のリスクが大きいのはローラポンプである。
誤り。遠心ポンプの流量は回転数だけで一義的に決まらず、前負荷・後負荷などの負荷条件に依存して変化する。したがって回転数に“正比例”とはいえない。
正しい。遠心ポンプは後負荷(下流側圧)が上昇するとポンプの圧流量曲線により流量が減少する特性を持つ。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
生体の誘電特性は周波数が上がると一般に低下し、代表的な分散としてα・β・γ分散がみられる。α分散は低周波域(おおむね数Hz〜数kHz)で、膜表面や電極界面でのイオンの集散・拡散(二重層形成など)に起因する。β分散は細胞膜の絶縁層と細胞内外の電解質という層状構造に由来するMaxwell–Wagner型の界面分極で、数kHz〜数十MHzの範囲で顕著となる。γ分散は水分子の配向緩和(回転)に基づき、数GHz〜数十GHz(典型的には約20GHz付近)でみられる。このため「β分散は約GHzで生じる」は誤りで、GHz帯はγ分散の典型的領域である。なお、低周波で誘電率が大きく観測されるのは、界面分極が十分追従できるためであり、骨格筋は筋線維方向と横方向で導電性・誘電性が異なる強い異方性を示す。細胞膜は極めて薄い誘電体であり、コンデンサの関係式 $C=\varepsilon \\frac{S}{d}$ より大きな電気容量としてふるまう。
選択肢別解説
正しい。生体組織では低周波域で界面分極(Maxwell–Wagner分極)が十分に生じ、分極が増すことで実効的な誘電率が大きく評価される。周波数が上がると分極が追従できなくなり、誘電率は低下していく。
正しい。骨格筋は筋線維が一定方向に配列しており、線維方向は横方向より電気が流れやすい(導電率が高い)など、電気特性の異方性が大きいことが知られている。
正しい。細胞膜は非常に薄い脂質二重層という誘電体で、電気容量は $C=\varepsilon \\frac{S}{d}$ に従うため、厚さ $d$ が小さいほど容量は大きくなる。膜の薄さにより、細胞膜は大きな電気容量を示す。
正しい。α分散は低周波域(数Hz〜数kHz)でみられ、膜表面や界面におけるイオンの集散・拡散(二重層形成など)に起因する。
誤り。β分散は細胞膜由来のMaxwell–Wagner型界面分極で、典型的には数kHz〜数十MHzの周波数帯で生じる。GHz帯(約20GHz付近など)は主として水分子の配向緩和に基づくγ分散の領域であり、β分散ではない。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
トランジットタイム(時間差)型超音波血流計は、流れに沿う向きと逆向きの2経路で音波を伝播させ、その到達時間差から平均流速(および流量)を求める方式である。代表的な関係式は、入射角を $\theta$、音速を $c$、経路長を $L$、流速を $v$ とすると、順流方向 $t_{\downarrow}=\dfrac{L}{c+v\cos\theta}$、逆流方向 $t_{\uparrow}=\dfrac{L}{c-v\cos\theta}$、時間差 $\Delta t=t_{\uparrow}-t_{\downarrow}\approx\dfrac{2Lv\cos\theta}{c^2}$ で、流速が大きいほど $\Delta t$ は大きくなる。測定は広いビームで流路断面全体を音場内に含めることで、速度分布の影響を低減し断面平均に近い値を得る。一方、赤血球による散乱波の周波数シフト(ドプラ効果)を測るのはドプラ型血流計の原理であり、本方式とは異なる。体外循環回路(人工心肺、ECMO 等)では非侵襲に装着でき、標準的に用いられている。
選択肢別解説
正しい。時間差法では、流れに沿う向きと逆向きの双方へ超音波を送受し、それぞれの伝播時間を測って差分から流速を求める。
正しい。流路断面全体をカバーする広い音場(ワイドビーム)で計測し、速度分布の影響を受けにくい断面平均に近い値を得るのがトランジットタイム型の特徴である。
誤り。赤血球で散乱された超音波の周波数シフトを測るのはドプラ型の原理であり、トランジットタイム型は伝播時間差を測定する。
正しい。流速が増すと順流方向は到達時間が短く、逆流方向は長くなり、その時間差 $\Delta t\,(\approx 2Lv\cos\theta/c^2)$ は流速に比例して大きくなる。
正しい。体外循環(人工心肺、PCPS/ECMO など)の回路流量計測に広く用いられる実績がある。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
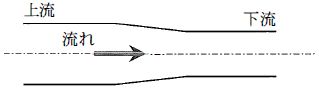
非圧縮性の水が層流を維持している条件では、連続の式 $A_1 v_1 = A_2 v_2$ が成り立つ。断面積が上流の半分($A_2=\tfrac{1}{2}A_1$)になると、下流の流速は $v_2=2v_1$ と2倍に増加する。層流の管路抵抗はハーゲン・ポアズイユの法則 $R=\tfrac{8\mu L}{\pi r^4}$ に従い半径の4乗に反比例する。断面積 $A=\pi r^2$ が1/2になると半径は $r_2=\tfrac{r_1}{\sqrt{2}}$ なので、$R_2/R_1=(r_1/r_2)^4=(\sqrt{2})^4=4$。よって下流では流速は2倍、管路抵抗は4倍となる。
選択肢別解説
誤り。断面積が1/2になると連続の式より流速は2倍になる。さらに半径が $1/\sqrt{2}$ 倍なので抵抗は $(\sqrt{2})^4=4$ 倍であり、$1/16$ 倍にはならない。
誤り。連続の式により下流の流速は2倍であって1/2倍ではない。抵抗も半径の4乗に反比例するため4倍に増加し、1/4倍にはならない。
誤り。流速は2倍であり1/2倍ではない。抵抗は4倍に増加するため1/2倍にはならない。
誤り。断面積1/2では流速は2倍にとどまり4倍にはならない。また抵抗は半径の4乗則より4倍であり2倍ではない。
正しい。断面積1/2なら連続の式で流速は2倍。ハーゲン・ポアズイユの法則 $R=\tfrac{8\mu L}{\pi r^4}$ より、$A\propto r^2$ から $r$ は $1/\sqrt{2}$ 倍となり、抵抗は $(\sqrt{2})^4=4$ 倍に増加する。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
生体組織に入射した光は、主に吸収・散乱・反射・屈折の相互作用を受ける。吸収はヘモグロビンやメラニンなどの色素や水分子によって光エネルギーが熱・化学エネルギー等に変換され、強度が減衰する(Beer–Lambertの法則的挙動)。散乱は細胞・細胞小器官・コラーゲン線維・赤血球などの屈折率不均一により多重散乱が生じ、ビームは拡がり拡散的に伝搬する。境界面では一部が反射(Fresnel反射)するため透過光は減少し、屈折率の異なる媒質境界での入射ではスネルの法則に従い進行方向が変わる。媒質中の光速は屈折率 n により $v=c/n$ で与えられ、空気の n≈1 に対して生体組織の n は一般に 1 より大きいため、組織中の光速は空気中より遅い。よって「生体中では光速が空気中より大きい」という選択肢5が誤りである。
選択肢別解説
正しい。生体内のクロモフォア(例:ヘモグロビン、メラニン、水など)により光は吸収され、光強度は深さとともに減衰する。実効的には Beer–Lambert 則に従い、吸収係数が大きいほど減衰は強い。
正しい。生体組織は屈折率不均一を多く含むため多重散乱が卓越し、ビームは空間的に拡がって拡散的伝搬となる(特に可視〜近赤外域で顕著)。
正しい。組織表面や組織間の界面で反射(Fresnel反射)が生じ、その分だけ透過成分は減少する。反射率は入射角や屈折率差に依存する。
正しい。屈折率の異なる媒質境界に斜入射するとスネルの法則に従い進行方向が変わるため、光路は曲げられる。
誤り。媒質中の光速は $v=c/n$ で与えられ、組織の屈折率 n は空気(約1)より大きい。したがって生体組織中の光速は空気中より小さく(遅く)なる。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。