第3回国試午前54問の類似問題

血液について誤っているのはどれか。

1: 非ニュートン流体である。

2: 力学的に等方的である。

3: 比誘電率は周波数依存性がある。

4: 超音波伝搬速度は空気中よりも速い。

5: 吸光度は可視光領域でほぼ一定である。

直径1cmの大動脈内の血流速度が50cm/sであるときのレイノルズ数はどれか。ただし、血液密度は1.05×103 kg/m3 、血液の粘性率は3.0×10-3 Pa･s とする。（生体物性材料工学）

1: 1000

2: 1250

3: 1500

4: 1750

5: 2000

誤っているのはどれか。

1: 縦弾性係数の単位は［m］である。

2: ひずみの単位は無次元である。

3: 引張り応力は材料内部に働く単位面積あたりの力である。

4: せん断応力は荷重に対して平行な断面に働く応力である。

5: ポアソン比は横ひずみを縦ひずみで除した大きさである。

物理量と単位との組合せで誤っているのはどれか。（生体計測装置学）

1: 粘度 Pa・s

2: 熱容量 J/K

3: 力のモーメント N・m

4: 電界の強さ V・m

5: 放射照度 W/m2

正しいのはどれか。

1: 血漿はほぼニュートン流体と見なせる。

2: 水を多く含む生体軟組織のポアソン比はほぼ1である。

3: 組織のヤング率が大きいほど応力に対するひずみが大きい。

4: マックスウェルモデルは弾性要素と粘性要素が並列に接続されている。

5: 軟組織は膠原線維の割合が大きいほど伸展性が大きい。

生体組織の力学的性質について誤っているのはどれか。

1: 血漿は非圧縮性流体である。

2: 軟部組織は硬組織に比べヤング率が小さい。

3: 軟部組織のポアソン比はおよそ0.5である。

4: 大静脈でのレイノルズ数は上腕動脈でのレイノルズ数より小さい。

5: ヤング率が同じであれば、太い血管ほど脈波伝播速度は小さい。

物体の変形について誤っているのはどれか。

a: 荷重を除いたときに完全に元の形に戻る性質を弾性と呼ぶ。

b: 弾性限度内では荷重は変形量に比例する。

c: 弾性限度内の応力のひずみに対する比をフック率と呼ぶ。

d: 縦弾性係数が大きいほど体積弾性係数は小さい。

e: 弾性限度を超える荷重を加えると塑性変形を生じる。

1. a b　2. a e　3. b c　4. c d　5. d e

健常人の血液について正しいのはどれか。

a: 非ニュートン流体である。

b: 血漿はニュートン流体である。

c: ヘマトクリットが減少すると粘度は低下する。

d: 粘度は生理食塩液と等しい。

e: 粘度は温度に関わらず一定である。

1. a b c　2. a b e　3. a d e　4. b c d　5. c d e

内直径8mmの血管の中を粘性率が0.002Pa･s、密度が1060kg/m3の血液が平均速度0.2m/sで流れている時、おおよそのレイノルズ数はどれか。

1: 0.8

2: 8

3: 80

4: 800

5: 8000

定常流の定義として正しいのはどれか。

1: ある断面を単位時間内に通過する流体の量が時間的に変化しない。

2: 流速がどこでも同じ値をとる。

3: 連続の方程式が成り立つ。

4: ずり速度がどこでも同じ値をとる。

5: 流線が時間的に変化しない。

流れにおけるベルヌーイの定理を表す式について正しいのはどれか。 

a: 完全流体に適用される。 

b: 重力とは無関係である。 

c: 温度をパラメータとして含む。 

d: 連続の式を導くことができる。 

e: 力学的エネルギー保存則が適用される。 

1. a b　2. a e　3. b c　4. c d　5. d e

応力とひずみについて正しいのはどれか。

a: 応力は作用する荷重と断面積の積である。

b: ひずみは変形の度合いを比で表したものである。

c: 荷重と同一の方向に現れるひずみを縦ひずみという。

d: せん断応力によって生じるひずみを横ひずみという。

e: 弾性係数は応力とひずみの積である。

1. a b　2. a e　3. b c　4. c d　5. d e

定常流における連続の条件として一定でなければならないのはどれか。

1: 圧力と断面積との積

2: 圧力と断面積と密度との積

3: 圧力と流速と断面積との積

4: 流速と断面積と密度との積

5: 流速と断面積との積

フックの法則について正しいのはどれか。

a: 塑性変形に対して成り立つ。

b: 線形弾性変形に対して成り立つ。

c: 応力はひずみに比例する。

d: 材料の体積が変わらないことを表す。

e: 材料の粘性を表す。

1. a b　2. a e　3. b c　4. c d　5. d e

応力について正しいのはどれか。

a: 作用する力と断面積の積が応力である。

b: 応力と圧力は同じ単位で表せる。

c: 面に平行な方向の応力をせん断応力という。

d: 弾性係数はひずみと応力との関係を表す。

e: 穴のあいた板を引っ張ったときに生じる応力はどこでも同じ値である。

1. a b c　2. a b e　3. a d e　4. b c d　5. c d e

円管内の流れのレイノルズ数を算出するのに必要な因子はどれか。

a: 粘性係数

b: 流 速

c: 管 径

d: 管路長

e: 拡散係数

1. a b c　2. a b e　3. a d e　4. b c d　5. c d e

水の表面張力について誤っているのはどれか。 

1: 単位はN/mである。 

2: 毛管現象の要因である。 

3: 分子の凝集力によって生じる。 

4: 温度が高くなると小さくなる。 

5: 液滴の表面積を大きくするように働く。 

生体組織の力学的性質について誤っているのはどれか。

1: 血漿は非圧縮性流体である。

2: 大血管内の血液の流れは層流である。

3: 軟部組織のポアソン比はおよそ0.5である。

4: 軟部組織は硬組織に比べヤング率が小さい。

5: 筋のヤング率は直行方向より走行方向で大きい。

図のように水平に置かれた絞りのあるパイプに流体が流れている。絞りの前後の圧力差 P1 - P2 を表す式はどれか。ただし、流体の密度をρ、絞りの前の流速をV1、絞りの後の流速をV2とし、完全流体が定常流で流れているとする。

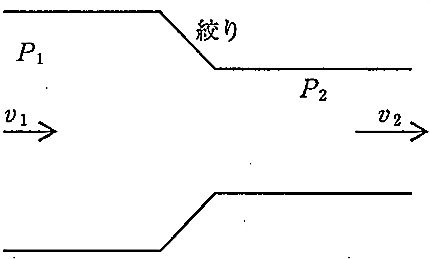
1: $ \frac {1}{2}\rho v^{2}_{1}$

2: $ \frac {1}{2}\rho v^{2}_{2}$

3: $ \frac {1}{2}\rho v_{1}v_{2}$

4: $ \frac {1}{2}\rho \left( v^{2}_{1}-v^{2}_{2}\right) $

5: $ \frac {1}{2}\rho \left( V^{2}_{2}-V^{2}_{1}\right) $

気体の圧力ｐ、体積Ｖ、物質量ｎ、気体定数Ｒ、温度Ｔとしたときに成り立つ法則ｐＶ＝ｎＲＴについて正しいのはどれか。

a: この法則はボイル・シャルルの法則と呼ばれる。

b: 物質量nは単位体積あたりの気体の質量である。

c: 気体常数Rは気体の種類によって異なる。

d: 温度Tは絶対温度である。

e: この法則が成り立つ気体は理想気体または完全気体と呼ばれる。

1. a b c　2. a b e　3. a d e　4. b c d　5. c d e