臨床工学技士問題表示
臨床工学技士国家試験
解説
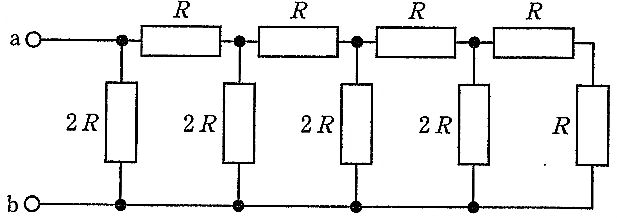
図の回路は、上側に直列のRが並び、各節点から下側母線(b)へ縦にシャント抵抗が接続されたラダー回路で、最右端だけシャントがR、それ以外は2Rとなっている。右端から順次合成すると、(1) 右端の横Rと縦Rは直列で2R、(2) これと左隣節点の縦2Rが並列で $R_p=\frac{2R\cdot 2R}{2R+2R}=R$、(3) 得られたRとその左の横Rが直列で2R、(4) これと次の縦2Rが並列で再びR…という操作を繰り返すと、入口(端子a)まで来たときの合成抵抗はRとなる。直列は $R_s=R_1+R_2$、並列は $R_p=\frac{R_1R_2}{R_1+R_2}$ を用いる。したがって端子ab間の合成抵抗はR。
選択肢別解説
ラダーを右端から順次簡約すると、各ステップで2R(直列)→R(並列)を繰り返し、入口ではRとなる。よって $\frac{1}{3}R$ は誤り。
同様に段ごとの合成で最終的にRに収束するため、 $\frac{1}{2}R$ は誤り。
右端の横Rと縦Rが直列で2R、これと左隣の縦2Rが並列でR、さらに左の横Rと直列で2R、次の縦2Rと並列でR…を繰り返すと、端子aから見た合成抵抗はRとなるため正しい。
段ごとの直列→並列の簡約を繰り返すと入口でRになる。2Rにはならないため誤り。
ラダー簡約の結果はRであり、3Rにはならないため誤り。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
患者測定電流(患者補助電流:Patient auxiliary current, PAC)は、装着部(適用部位)の機能上の理由で患者を介して意図的に流す微小電流を指し、増幅器入力のバイアス電流やインピーダンスプレチスモグラフィの励起電流などが含まれる。測定は規格の試験回路を用い、装着部の各部分(電極等)間に測定器を接続して行う。規格(IEC 60601-1/JIS T 0601-1)では、直流は電気分解による化学的損傷の懸念があるため許容値が厳しく、B/BF形では交流の許容値(例:0.1 mA)が直流(例:0.01 mA)より大きく、CF形では双方が等しい(例:0.01 mA)。したがって「交流の許容値は直流より低い」という記述は誤りである。
選択肢別解説
誤り。規格では一般に直流の許容値の方が厳しく、B/BF形では交流>直流(例:AC 0.1 mA、DC 0.01 mA)、CF形ではAC=DC(例:0.01 mA)。よって「交流の許容値は直流より低い」は成り立たない。
正しい。患者測定電流は機能上意図して流れる微小電流であり、増幅器入力段のバイアス電流のように測定系由来の電流も含まれる。
正しい。インピーダンスプレチスモグラフィや生体インピーダンス測定で用いる励起電流は、機能上意図して患者に流す電流であり、患者測定電流に含まれる。
正しい。患者測定電流は、装着部の部分(電極等)間を患者を介して流れる意図された電流として定義される。
正しい。患者測定電流の評価は、規格の試験回路(測定用器具)を装着部の部分間に接続して行う方法で規定されている。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
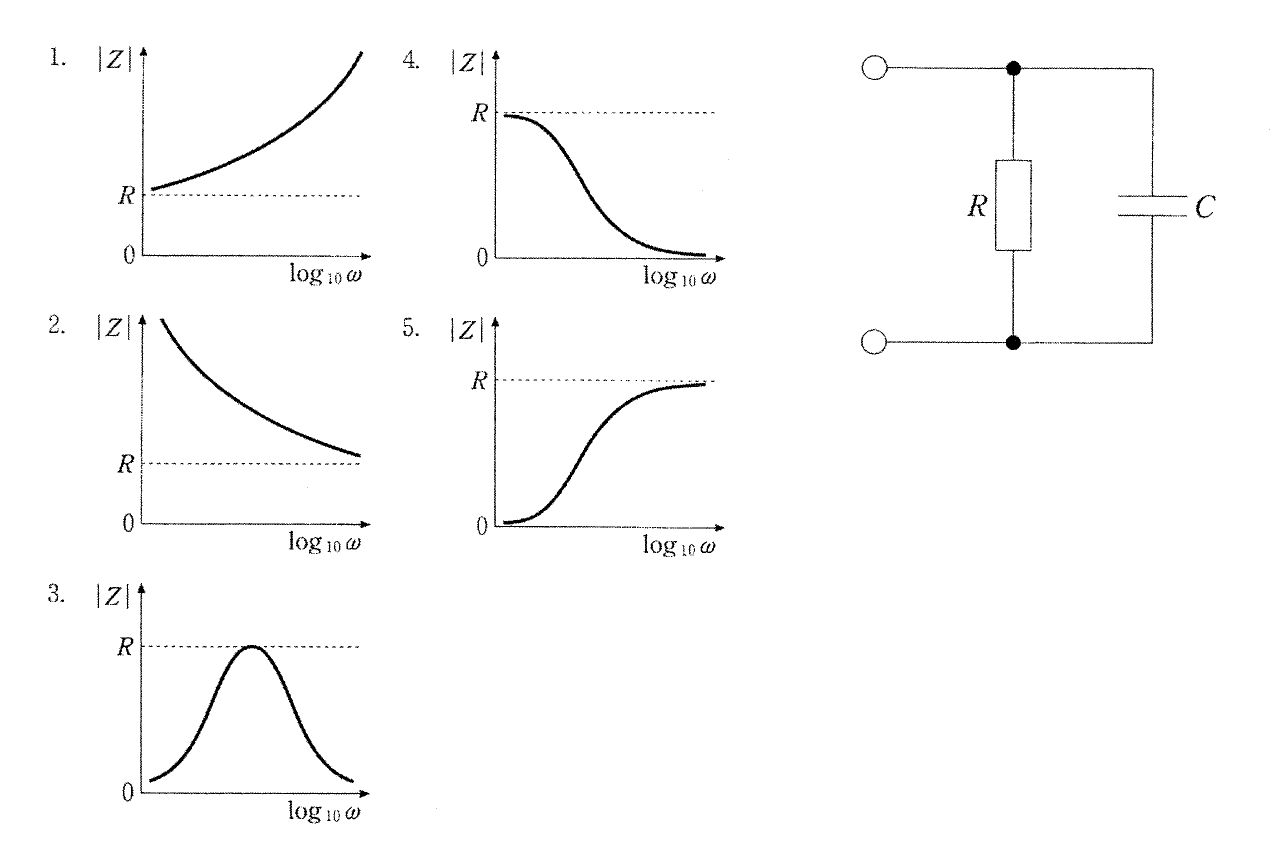
図の回路は抵抗RとコンデンサCの並列回路である。並列回路のアドミタンスは $Y=1/R+j\omega C$、したがってインピーダンスは $Z=1/Y$、その大きさは $|Z|=\dfrac{1}{\sqrt{(1/R)^2+(\omega C)^2}}=\dfrac{R}{\sqrt{1+(\omega RC)^2}}$ となる。よって、低周波域 ($\omega\to 0$) では $|Z|\to R$、高周波域 ($\omega\to \infty$) ではコンデンサが短絡的に振る舞い $|Z|\to 0$。対数横軸のボード線図でも単調減少し、Rから始まって0へ近づく形となる。画像の選択肢ではこの形状を示すのは4である。
選択肢別解説
図1は周波数とともに |Z| が単調増加する形で、低周波側でR付近から出発して高周波で増大している。RC並列では $|Z|=R/\sqrt{1+(\omega RC)^2}$ のため、周波数増加で必ず減少し0へ近づくので不適。
図2は低周波でRより大きな値から減少し、高周波でもRへは収束していない。RC並列では $\omega\to 0$ で厳密にR、$\omega\to \infty$ で0に近づくため、この形は不適。
図3は中間周波数でピーク(共振)を示す形。抵抗とコンデンサのみのRC回路は共振を生じないため不適。
図4は低周波でRから始まり、周波数増加とともに単調に減少して0へ近づく形。RC並列回路の $|Z|=R/\sqrt{1+(\omega RC)^2}$ の特性と一致する。
図5は低周波で0付近から増加し、高周波でRに近づく形。RC並列では低周波でR、高周波で0に近づくため、この挙動は逆で不適。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
電池は起電力(開放電圧)Eと内部抵抗rが直列につながった等価回路で表せる。負荷抵抗Rを接続すると回路電流はオームの法則より $I = \frac{E}{r+R}$。これをRについて解くと $R = \frac{E}{I} - r$。与えられた値 E=9.0\,V、r=20\,\Omega、I=300\,mA=0.30\,A を代入すると $R = \frac{9.0}{0.30} - 20 = 30 - 20 = 10\,\Omega$。したがって負荷抵抗は10\,\Omega(選択肢3)が正しい。
選択肢別解説
誤り。R=2\,\Omega とすると電流は $I=\frac{E}{r+R}=\frac{9}{20+2}=\frac{9}{22}\approx0.409\,A$ となり、与えられた0.300\,Aと一致しない。
誤り。R=6\,\Omega では $I=\frac{9}{20+6}=\frac{9}{26}\approx0.346\,A$ で、0.300\,Aとは一致しない。
正しい。式 $R=\frac{E}{I}-r$ により $R=\frac{9.0}{0.30}-20=10\,\Omega$。検算でも $I=\frac{9}{20+10}=\frac{9}{30}=0.30\,A$ と一致する。
誤り。R=20\,\Omega では $I=\frac{9}{20+20}=\frac{9}{40}=0.225\,A$ となり、0.300\,Aと一致しない。
誤り。R=30\,\Omega では $I=\frac{9}{20+30}=\frac{9}{50}=0.18\,A$ で、0.300\,Aと一致しない。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
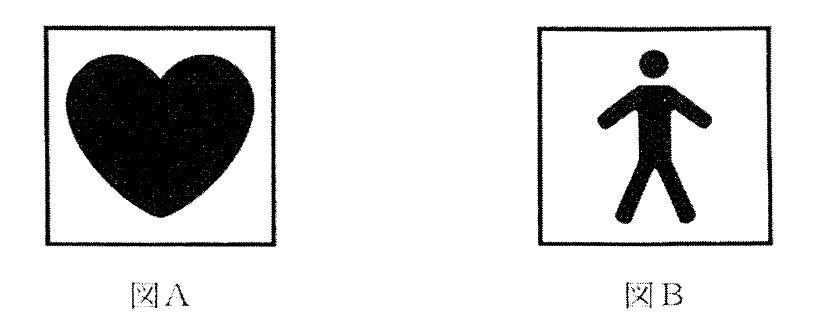
図AはCF形装着部(心臓に直接適用可能)、図BはBF形装着部(体表・体腔適用だが心臓非接続)を示す図記号である。装着部の型が異なっても、IEC 60601-1/JIS T 0601-1で共通の許容値が定められている項目があり、代表的には次の3つが共通となる。外装漏れ電流の単一故障状態は0.5 mA、患者測定電流(直流)の正常状態は0.01 mA、接地漏れ電流の正常状態は0.5 mA。よって1、2、5が『共通する』に該当する。一方、患者測定電流(交流)の単一故障状態はBF形0.5 mA、CF形0.05 mAで異なり、患者漏れ電流IIIもBF形5 mA、CF形0.05 mAで異なるため共通しない。
選択肢別解説
正しい。外装漏れ電流の単一故障状態での許容値は、BF形・CF形いずれの装着部でも0.5 mAで共通(IEC 60601-1/JIS T 0601-1)。
正しい。患者測定電流(直流)の正常状態での許容値はBF形・CF形ともに0.01 mAで共通である。
誤り。患者測定電流(交流)の単一故障状態は装着部で異なり、BF形0.5 mA、CF形0.05 mAで共通ではない。
誤り。患者漏れ電流IIIの許容値は装着部で異なる設定で、単一故障状態ではBF形5 mA、CF形0.05 mAなどと大きく差があり、共通ではない。
正しい。接地漏れ電流の正常状態での許容値はBF形・CF形ともに0.5 mAで共通である。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
非接地配線方式(医用IT配電システム)は、絶縁変圧器で電源系を大地から浮かせ、絶縁監視装置で対地インピーダンス(絶縁状態)を常時監視する方式である。主目的は一線地絡が起きても遮断せずに電源供給を継続すること(継続供電)である。絶縁監視装置の警報基準は一般に対地インピーダンスが約 $50 \\text{k}\\Omega$ 以下となったときで、商用 $100 \\text{V}$ 換算では $I=V/R=100/50{,}000=2 \\text{mA}$ 程度で警報となる。多数のME機器を同一系統に接続すると、それぞれの漏れ経路や絶縁抵抗が並列合成されて対地インピーダンスが低下し、警報が出やすくなる。一方、絶縁変圧器の一次・二次間の容量性漏れ電流は通常 $0.1 \\text{mA}$(100 $\\mu$A)以下が規定であり、10 $\\mu$Aという水準は過度に厳しい。また、非接地配線方式であっても機器の外装・等電位ボンディングを含む保護接地設備は必須である。
選択肢別解説
誤り。医用IT用の絶縁変圧器では一次・二次間の容量性漏れ電流は通常 $0.1 \\text{mA}$(100 $\\mu$A)以下とされる。選択肢の10 $\\mu$A以下は過度に厳しく、規定と一致しない。
誤り。絶縁監視装置の警報は、一般に対地インピーダンスが $50 \\text{k}\\Omega$ 以下になると発生する。商用 $100 \\text{V}$ 換算では $I=100/50{,}000=2 \\text{mA}$ 程度であり、1 mA超ではなく約2 mA相当が基準となる。
正しい。非接地配線方式の主目的は、一線地絡時でもブレーカを遮断せず医療行為を止めないよう電源供給を継続すること(継続供電)である。
正しい。多数のME機器を同一系統に接続すると、それぞれの漏れ経路・絶縁抵抗が並列となり合成対地インピーダンスが低下し、監視装置の警報(例: $50 \\text{k}\\Omega$ 以下)に到達しやすくなる。
誤り。非接地配線方式は電源系を大地から浮かせる方式だが、機器外装の感電防止や等電位化のための保護接地設備は必要であり、不要ではない。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
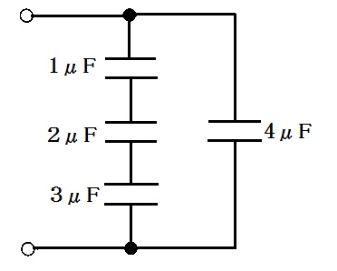
図より、1 μF・2 μF・3 μF は直列、これらの合成容量 C_s と 4 μF が並列である。直列合成は $\tfrac{1}{C_s}=\tfrac{1}{1}+\tfrac{1}{2}+\tfrac{1}{3}=\tfrac{11}{6}$ より $C_s=\tfrac{6}{11}\,\mu\mathrm{F}\approx0.545\,\mu\mathrm{F}$。並列では単純加算なので、全体の合成容量 $C=C_s+4\approx0.545+4=4.545\,\mu\mathrm{F}$。与えられた選択肢の中では 5 μF が最も近い。なお、直列部は 1 μF 未満であるため合成容量は 5 μF 未満になり、10 μF など大き過ぎる値はあり得ない。
選択肢別解説
0.42 μF は直列部分 $C_s\approx0.545\,\mu\mathrm{F}$ よりも小さく、全体は $C=C_s+4\approx4.545\,\mu\mathrm{F}$ であるため不適。
0.52 μF は直列合成のみを答えた近い値だが、実際はこれに 4 μF が並列に加わるため全体は約 4.545 μF。誤り。
2.4 μF は直列・並列いずれの正しい計算結果とも合致しない。正しい合成は約 4.545 μF。
正解。直列合成 $C_s=\tfrac{6}{11}\,\mu\mathrm{F}\approx0.545$ を 4 μF と並列加算して $C\approx4.545\,\mu\mathrm{F}$。提示選択肢中では 5 μF が最も近い。
10 μF は過大。直列部は 1 μF 未満であり、並列加算しても合計は 5 μF 未満(約 4.545 μF)となる。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
誤りは1。ペースメーカの出力パルス振幅(電圧)は、500 $\Omega$ 程度の負荷抵抗を介してオシロスコープまたはペースメーカアナライザで測定するのが基本で、周波数カウンタはパルスの周期・周波数(レート)測定用であり振幅測定には不適切である。除細動器の出力波形は瞬時現象のため、50 $\Omega$ 程度のダミー負荷に接続しメモリ型オシロスコープで単発波形を捕捉するのが適切。電気メスの出力電力は高周波で誘導の影響を避ける必要があるため無誘導抵抗器を負荷として用い、流れる電流から $P=I^2R$ で算出する。輸液ポンプの精度(送液量)はメスシリンダで回収量を測って設定値と比較する。人工心肺(に限らず医用機器)の絶縁抵抗は絶縁抵抗計(メガー)で測定する。
選択肢別解説
誤り。周波数カウンタはパルスの周波数(レート)や周期の測定器であり、振幅(電圧)を測定できない。ペースメーカの出力パルス振幅は、500 $\Omega$ 程度の負荷抵抗を介してオシロスコープまたはペースメーカアナライザで電圧波形を観測して求めるのが適切。
正しい。除細動器の出力は瞬時に発生する単発波形であるため、50 $\Omega$ 程度のダミー負荷(模擬胸部インピーダンス)に接続し、メモリ型オシロスコープで波形を保持・確認する。エネルギーチェッカの波形出力端子を用いる方法もある。
正しい。電気メス(ESU)の出力電力測定では、高周波での誤差を避けるため無誘導抵抗器を負荷として用い、負荷に流れる電流から $P=I^2R$ で電力を算出する。実務上は無誘導抵抗器に加えて高周波対応の電流計等も併用するが、必要な機材として無誘導抵抗器の選定は妥当。
正しい。輸液ポンプの精度(送液量・流量)は、メスシリンダで一定時間に送られた液量を回収・計量し、設定値と比較して評価する。専用の輸液ポンプチェッカを用いる方法もある。
正しい。人工心肺装置の絶縁抵抗測定には、絶縁抵抗計(メガー)を用いて、電源回路と筐体(外装)間など所定箇所の絶縁を測るのが標準的手順である。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。

解説
提示図記号は「耐除細動形のCF形装着部」を示す。CF形は心臓に直接つながる可能性のある装着部に適用され、除細動時の高電圧・高電流から患者・機器を保護する設計(耐除細動)を満たしている。したがって、除細動の際に誘導コードを外す必要はないため、選択肢5は誤り。他の記述は、CF形・耐除細動形の特性および漏れ電流(接触電流)の規格要件に合致しており妥当である。接触電流(外装漏れ電流)の許容値は装着部の種別に依存せず、IEC 60601-1系規格ではおおむね正常状態100 µA、単一故障状態500 µAの水準が用いられる。
選択肢別解説
正しい。CF形装着部を備える心電図モニタは、通常の表面(胸部)誘導のモニタリングが可能である。耐除細動形であれば除細動時の保護も備える。
正しい。CF形は心臓に直接接続され得る装着部に要求される最も厳しい安全条件を満たす分類であり、ペーシングリードなどを介した心内心電図の誘導に適合し得る(機能の有無は機種依存だが、安全性分類としては許容される)。
正しい。ICUでは除細動の可能性があるため、除細動時の過大電圧に耐える『耐除細動形CF形』の心電図モニタが望ましい。誘導コードを外さずに連続監視を継続できる利点がある。
正しい。外装漏れ電流(接触電流)は装着部の種別(B/BF/CF)に依存せず同一水準の規格値が適用され、一般に正常状態約100 µA、単一故障状態約500 µAが上限である。したがって人工呼吸器等の他機器と『同程度でよい』という表現は妥当である。
誤り。図記号は『耐除細動形のCF形装着部』を示すため、除細動の際に誘導コードを外す必要はない(機器は除細動パルスに耐える設計)。ただし臨床上は電極位置の適切な配置や接触回避などの安全手順は必要である。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
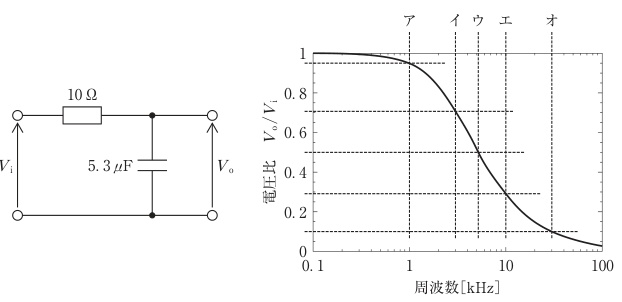
図の回路は抵抗R=10\,\Omega とコンデンサC=5.3\,\mu Fを直列にし、その分圧点(コンデンサ両端)から出力を取り出すRCローパスフィルタである。伝達関数は $H(j\omega)=\dfrac{Z_C}{R+Z_C}=\dfrac{1}{1+j\omega RC}$、振幅特性は $\left|\dfrac{V_o}{V_i}\right|=\dfrac{1}{\sqrt{1+(\omega RC)^2}}$。遮断周波数は $\omega RC=1$(すなわち $\left|V_o/V_i\right|=1/\sqrt{2}\approx0.707$、-3 dB)で定義され、数値的には $f_c=\dfrac{1}{2\pi RC}=\dfrac{1}{2\pi\times10\times5.3\times10^{-6}}\approx3.0\,\text{kHz}$。右図の周波数特性で0.7付近で曲線と交わる位置に引かれた縦線が遮断周波数であり、ラベル「イ」に相当する。
選択肢別解説
アは低周波側で $|V_o/V_i|$ が0.9〜1付近の通過域に位置しており、-3 dB点(0.707)ではないため遮断周波数を示さない。
イは曲線が0.707(=1/\sqrt{2})に達する位置に対応し、ローパスフィルタの遮断周波数の定義 $\omega RC=1$ に合致する。計算でも $f_c\approx3.0\,\text{kHz}$ となり、グラフ上の「イ」と一致する。
ウはイより高周波側で $|V_o/V_i|<0.7$ の減衰域(阻止域)にあり、遮断周波数そのものではない。
エはさらに高周波側で振幅は0.7より明確に小さく、減衰域の点であるため遮断周波数ではない。
オは高周波端で強く減衰しており、遮断周波数(-3 dB点)ではない。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。