臨床工学技士問題表示
臨床工学技士国家試験
検索元問題
第30回 午前 第39問
20件の類似問題
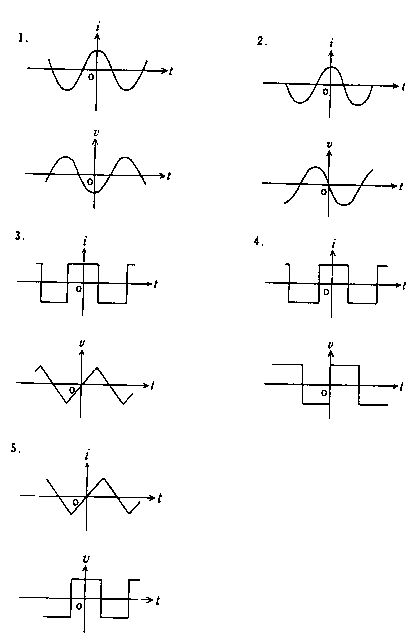
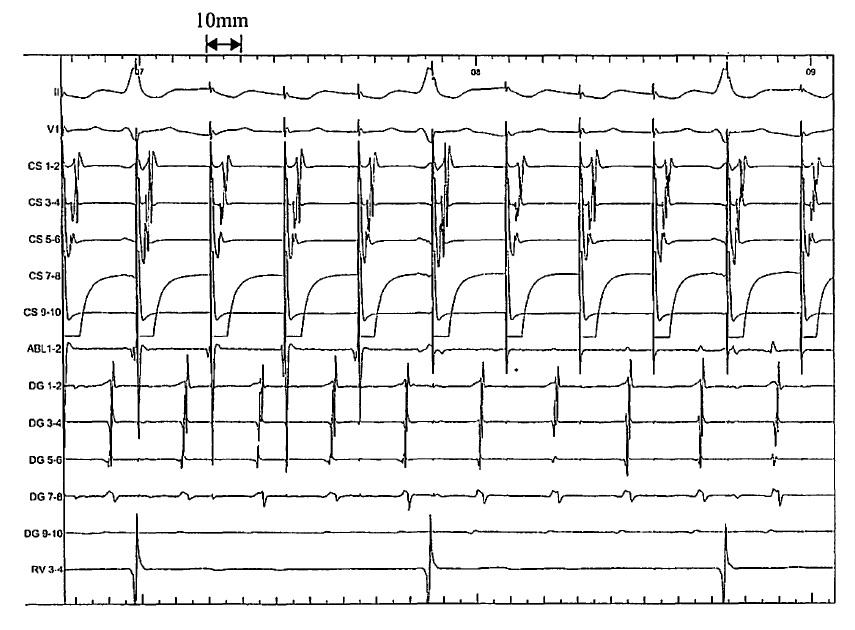
図は大動脈圧とその平均血圧の波形である。平均血圧を得るための回路として正しいのはどれか。...
広告
50
臨床工学技士国家試験 -
第35回 午前
重要度:低
正答率:46%
類似度 51.7%
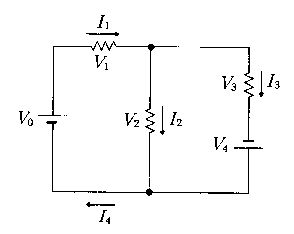
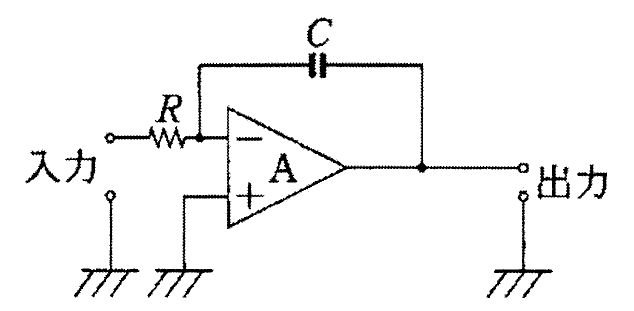
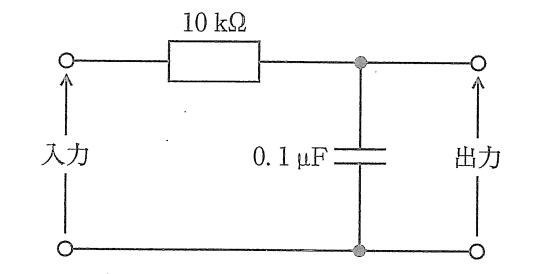
図の回路について誤っているのはどれか。
a
時定数は1msである。
b
遮断周波数は約160Hzである。
c
遮断周波数より十分に高い周波数では積分回路として動作する。
d
遮断周波数で出力電圧は入力電圧の1/2に減衰する。
e
入出力電圧の位相差は周波数によらず一定である。
組み合わせ:
1. a b
2. a e
3. b c
4. c d
5. d e
17
臨床工学技士国家試験 -
第18回 午後
類似度 51.6%
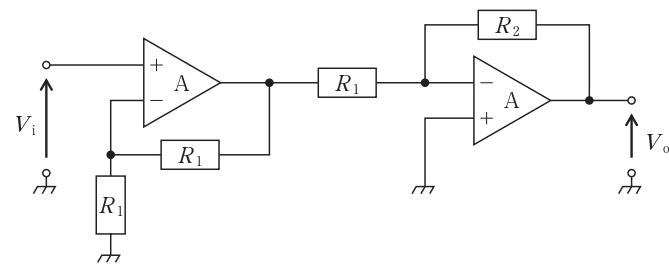
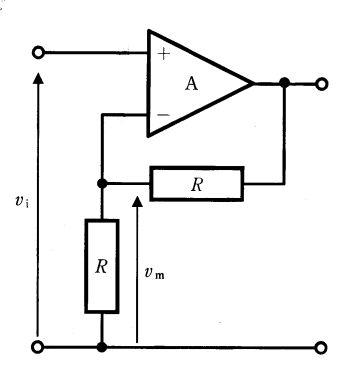
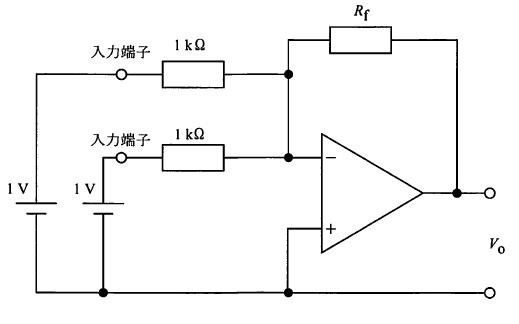
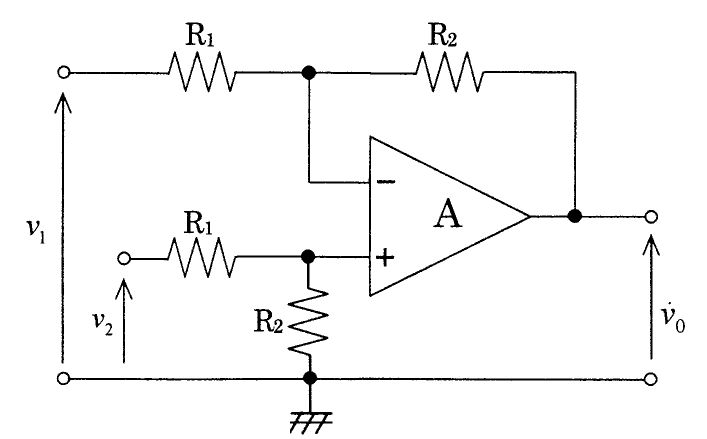
図の回路において二つの入力V1、V2とVoの関係を表す式はどれか。ただし、Aは理想演算増幅器とする。(電子工学)
1
$V_{0}=\frac {R_{1}+R_{2}}{R_{1}}\left( V_{2}-V_{1}\right) $
2
$V_{0}=\frac {R_{1}+R_{2}}{R_{2}}\left( V_{2}-V_{1}\right) $
3
$V_{0}=\frac {R_{1}+R_{2}}{R_{2}-R_{1}}\left( V_{2}-V_{1}\right) $
4
$V_{0}=\frac {R_{1}}{R_{2}}\left( V_{2}-V_{1}\right) $
5
$V_{0}=\frac {R_{2}}{R_{1}}\left( V_{2}-V_{1}\right) $
広告
7
第二種ME技術認定試験 -
第30回 午前
類似度 51.6%
血液循環の正しい順路はどれか。
1
大静脈→右心房→右心室→肺動脈→肺→肺静脈→左心房→左心室→大動脈
2
大静脈→右心房→右心室→肺静脈→肺→肺動脈→左心房→左心室→大動脈
3
大静脈→右心室→右心房→肺動脈→肺→肺静脈→左心室→左心房→大動脈
4
大静脈→左心室→左心房→肺静脈→肺→肺動脈→右心室→右心房→大動脈
5
大静脈→左心房→左心室→肺動脈→肺→肺静脈→右心房→右心室→大動脈
61
臨床工学技士国家試験 -
第17回 午前
正答率:83%
類似度 51.6%
科目:
観血式血圧計に関係があるのはどれか。
a
マイクロホン
b
マンシェット
c
トノメータ
d
カテーテル
e
ダンピングデバイス
組み合わせ:
1. a b
2. a e
3. b c
4. c d
5. d e
70
臨床工学技士国家試験 -
第33回 午後
重要度:最重要
正答率:68%
類似度 51.6%
科目:
人工心肺回路の動脈フィルタについて正しいのはどれか。
a
メッシュサイズは 200?400 nm である。
b
親水性のメッシュが使用される。
c
血液は上部から流入し、下部から流出していく。
d
回路の最後に装着する。
e
エアトラップと同様の構造である。
組み合わせ:
1. a b
2. a e
3. b c
4. c d
5. d e
広告
2
臨床工学技士国家試験 -
第10回 午後
正答率:50%
類似度 51.5%
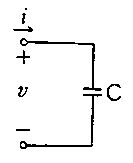
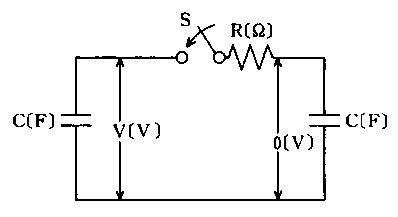
図の回路でスイッチSを閉じてから充分時間が経った後、回路全体に蓄えられるエネルギーはどれか。 ただし、両コンデンサは無損失とする。また、図中の電圧はスイッチを閉じる前の値である。
1
\frac{1}{2}CV^2\ J$
2
$\frac{1}{4}CV^2J$
3
$C^2V^2J$
4
$\frac{1}{2}C^2V\ J$
5
$\frac{1}{4}C^2V J$
56
臨床工学技士国家試験 -
第12回 午前
正答率:31%
類似度 51.4%
電磁血流計について正しいのはどれか。
a
血流によって発生する電流を計測する。
b
1心拍ごとの脈動血流量を測定できる。
c
磁界が血流の方向と直角になるようにプローブを装着する。
d
カフ型プローブの内径は血管外径より約10%小さいものを使う。
e
カフ型プローブの電極は血液と接触させる。
組み合わせ:
1. a b c
2. a b e
3. a d e
4. b c d
5. c d e
広告
35
臨床工学技士国家試験 -
第21回 午後
正答率:82%
類似度 51.3%
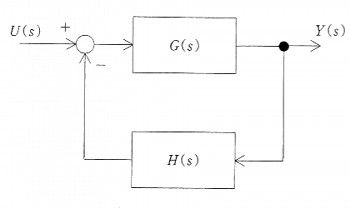
図のシステム伝達関数はどれか。
1
$\frac {1}{G\left( s\right) H\left( s\right) }$
2
$\frac {G\left( s\right) }{1-G\left( s\right) H\left( s\right) }$
3
$\frac {G\left( s\right) }{1+G\left( s\right) H\left( s\right) }$
4
$\frac {G\left( s\right) H\left( s\right) }{1-G\left( s\right) H\left( s\right) }$
5
$\frac {G\left( s\right) H\left( s\right) }{1+G\left( s\right) H\left( s\right) }$
広告