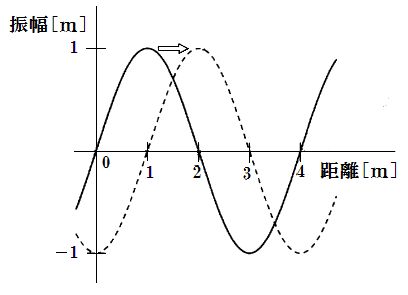
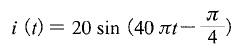第35回ME2午前40問の類似問題
国試第21回午後:第70問
ばね定数kのバネと質量mの質点を組み合わせて、図のようなバネ・質点系を作った。固有振動数が最も高い系はどれか。
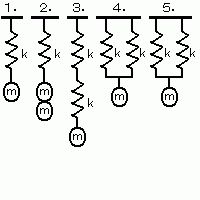
- 答え:4
- 科目:医用機械工学 /医用機械工学 /力学の基礎
- 重要度:集計中
- 類似問題を見る
- この問題について報告する
国試第27回午前:第80問
バネを鉛直に保ち、下端におもりを取付け、上端を一定振幅で上下に振動させる。周波数を徐々に変化させたとき、正しいのはどれか。
1: 周囲に抵抗がない場合、おもりの振幅は周波数によらず上端の振幅と等しい。
2: 周囲に抵抗がない場合、上端の振幅とおもりの振幅の比は周波数によらず一定である。
3: 周囲に抵抗がある場合、おもりの振動の周波数は上端の周波数よりも低い。
4: 周囲に抵抗がある場合、加速度が一定になる周波数がある。
5: 周囲に抵抗がある場合、ある周波数でおもりの振幅が最大になる。
国試第12回午後:第72問
図のようにバネ(①)におもりをつけたときl〔m〕伸びて静止した(②)。そのおもりをバネの自然長まで戻したところ(③)で手を放す。その直後の運動について正しいのはどれか。
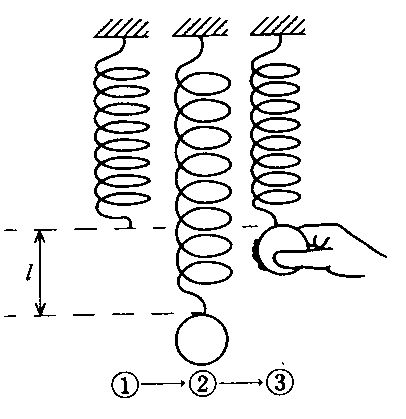
1: バネは直ちにl〔m〕伸びてそこで静止する。
2: バネは0.5 l〔m〕の振幅で持続振動する。
3: バネが自然長に戻ったところで速度が最大になる。
4: 振動の振幅とおもりの重さとは関係がない。
5: バネは減衰振動する。
- 答え:不適切問題
- 科目:医用機械工学 /医用機械工学 /力学の基礎
- 重要度:集計中
- 類似問題を見る
- この問題について報告する
国試第29回午前:第84問
直線上を一定速度v で移動する振動数f の音源が、静止した観測者に接近し、そのまま同じ速度で遠ざかった。音源の通過前後で観測される音の振動数の差を表す式はどれか。ただし音速をc とする。
1: $\frac {2v^{2}}{c^{2}}f$
2: $\frac {v\left( 2c-v\right) }{c\left( c-v\right) }f$
3: $\frac {2cv}{\left( c+v\right) \left( c-v\right) }f$
4: $\frac {2v}{c}f$
5: $\frac {v\left( 2c+v\right) }{c\left( c+v\right) }f$