第22回国試午前83問の類似問題

波動において角振動数をω, 振動数をf、速度をv 、波長をλとするとき周期はどれか。

1: 2πf

2: 1/f

3: λ/f

4: λω

5: f v

波の伝搬速度ｖ、周期Ｔ、振動数ｆ、角振動数ｗ、波長λの関係として正しいのはどれか。

a: v=λf

b: w=2πf

c: λ=v/T

d: f=vT

e: T=1/f

1. a b c　2. a b e　3. a d e　4. b c d　5. c d e

正弦波が一定速度v、周波数fで進むとき、周期T、角振動数ω、波長λ、波数Kの間の関係式で誤っているのはどれか。（医用機械工学）

1: $ \omega=2\pi{f}$

2: $ T=\frac{1}{f}$

3: $ v=\lambda{f}$

4: $ k=\frac{2\pi}{\lambda}$

5: $ f=\frac{k}{\pi}$

波動について正しいのはどれか。

a: 二つの波動が重なると波動の散乱が起こる。

b: 縦波と横波の伝搬速度は同じである。

c: 波動の伝搬速度をv、振動数をf、波長をλとするとv=λfである。

d: 波動の干渉によって周期的な腹と節を有する定常波が生じる。

e: 弾性体の棒の中を伝わる縦波の伝搬速度はヤング率の平方根に反比例する。

1. a b　2. a e　3. b c　4. c d　5. d e

波動について正しいのはどれか。

a: 二つの波動が重なると波動の散乱が起こる。

b: 縦波と横波の伝搬速度は同じである。

c: 波動の伝搬速度を v、振動数をf、波長をλとするとv=λfであ る。

d: 波動の干渉によって周期的な腹と節を有する定常波が生じる。

e: 弾性体の棒の中を伝わる縦波の伝搬速度はヤング率の平方根 に反比例する。

1. a b　2. a e　3. b c　4. c d　5. d e

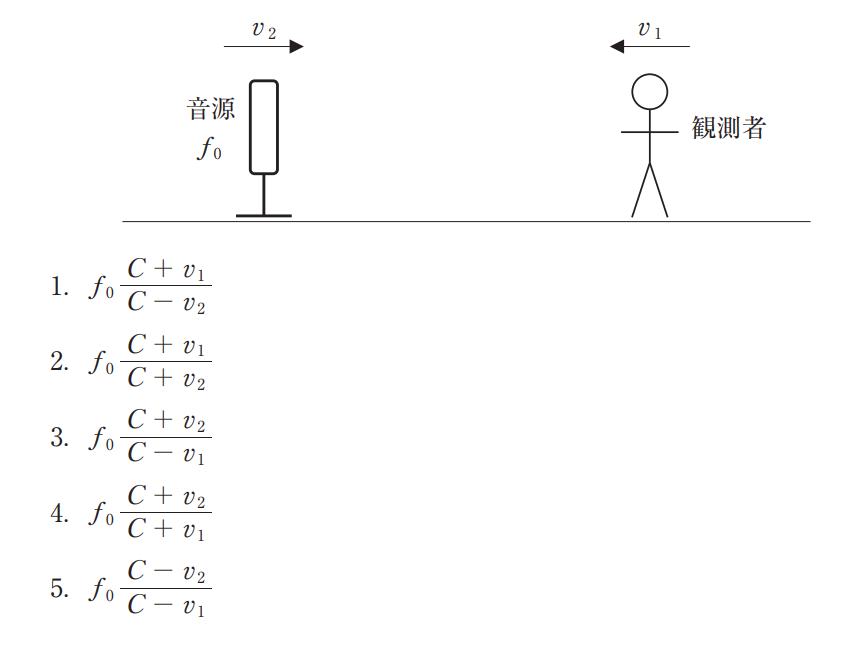
直線上を一定速度v で移動する振動数f の音源が、静止した観測者に接近し、そのまま同じ速度で遠ざかった。音源の通過前後で観測される音の振動数の差を表す式はどれか。ただし音速をc とする。

1: $\frac {2v^{2}}{c^{2}}f$

2: $\frac {v\left( 2c-v\right) }{c\left( c-v\right) }f$

3: $\frac {2cv}{\left( c+v\right) \left( c-v\right) }f$

4: $\frac {2v}{c}f$

5: $\frac {v\left( 2c+v\right) }{c\left( c+v\right) }f$

図のように、直線上を観測者と振動数f0の音源が互いに近づきながら移動している。観測者の速さをv1、音源の速さをv2とするとき、観測者の聞く音の振動数はどれか。ただし、音速をCとする。 

バネにおもりをつけて単振動を起こしたとき、周期T［s］を表す式はどれか。ただし、バネ定数をk［N/m］、おもりの質量をm［kg］とする。

図の波を表わす式はどれか。

x軸の正の向きに一定の進行速度vで進む振幅Aの波について、任意の時刻tにおける任意の点xでの状態がy（x，t）＝Asin（ωt－kx）で表されるとき、正しいのはどれか。ただし、fは振動数、λは波長、Tは周期とする。

a: 29

b: ω=2πf

c: λ=2πk

d: λ=vf

e: v=λT

1. a b　2. a e　3. b c　4. c d　5. d e

正しいのはどれか。

a: 繰返し方形波の周波数スペクトルを求めるには逆フーリエ変換を用いる。

b: 角周波数ωと周波数 f との関係はf =2πωで表される。

c: 時系列信号をフーリエ変換すると周波数成分を知ることができる。

d: 角周波数ωの正弦波(sin ωt)は一つの周波数成分で構成される。

e: 繰返し三角波には基本波以外に高調波成分が含まれる。

1. a b c　2. a b e　3. a d e　4. b c d　5. c d e

正しいのはどれか。

a: 繰返し方形波の周波数スペクトルを求めるには逆フーリエ変換を用いる。

b: 角周波数ωと周波数fとの間の関係はf=2πωで表される。

c: 時系列信号をフーリエ変換すると周波数成分を知ることができる。

d: 角周波数ωの正弦波(sinωt)は一つの周波数成分で構成される。

e: 繰返し三角波には基本波以外に高調波成分が含まれる。

1. a b c　2. a b e　3. a d e　4. b c d　5. c d e

正しいのはどれか。

a: 繰返し方形波の周波数スペクトルを求めるには逆フーリエ変換を用いる。

b: 角周波数ωと周波数fとの間の関係は で表される。

c: 時系列信号をフーリエ変換すると周波数成分を知ることができる。

d: 角周波数ωの正弦波(sinωt)は一つの周波数成分で構成される。

e: 繰返し三角波には基本波以外に高調波成分が含まれる。

1. a b c　2. a b e　3. a d e　4. b c d　5. c d e

正しいのはどれか。

a: 時系列信号をフーリエ変換すると周波数成分を知る事ができる。

b: 繰り返し方形波の周波数スペクトルを求めるには逆フーリエ変換を用いる。

c: 角周波数ωと周波数fとの間の関係はf=2πωで表される。

d: 角周波数ωの正弦波(sinωt)は一つの周波数成分で構成される。

e: 繰り返し三角波には基水波以外に高調波成分が含まれる。

1. a b c　2. a b e　3. a d e　4. b c d　5. c d e

共振周波数がfであるRLC直列回路がある。Cを求める関係式はどれか。

1: $ \frac {1}{2\pi fL}$

2: $ \frac {1}{4\pi fL}$

3: $ \frac {L}{2\pi fL}$

4: $ \frac {L}{4\pi f^{2}}$

5: $ \frac {1}{4\pi ^{2}f^{2}L}$

共振周波数がfであるRLC直列回路がある。Cを求める式はどれか。