第32回国試午後46問の類似問題

6cm離れた2点A、BにそれぞれQ[C]、4Q[C]の正の点電荷がある。3個目の点電荷を線分AB上に置くとき、これに働く力がつりあうAからの距離[cm]はどれか。

1: 0

2: 1.2

3: 1.5

4: 2

5: 3

半径r［m］、長さL［m］、電気抵抗0.2［Ω］の導線がある。同一材料で作られた2r、長さ8Lの導線の電気抵抗［Ω］はいくらか。

1: 0.1

2: 0.2

3: 0.4

4: 0.8

5: 1.0

図のように、巻数nの空心コイルに周波数fの交流電圧Vを加え、電流Iを流したとき、正しいのはどれか。

1: 巻数nを増加すると、電流Iは減少する。

2: コイル径を大きくすると、電流Iは増加する。

3: コイルに鉄心を入れると、電流Iは増加する。

4: 周波数fを高くすると、電流Iは増加する。

5: 電圧Vを高くすると、電流Iは減少する。

図のPN接合で正しいのはどれか。

a: 多数キャリアAには右方向に力が作用する。

b: 多数キャリアBは電子である。

c: 電圧Eを高くしていくと降伏現象が生じる。

d: 電圧Eを高くすると空乏層が小さくなる。

e: 電圧Eを高くすると拡散電位が高くなる。

1. a b　2. a e　3. b c　4. c d　5. d e

真空中で正三角形の頂点A、B、Cに電荷$Q_A$、$Q_B$、$Q_C$がある。$Q_A$、$Q_B$はいずれも1C（クーロン）、$Q_C$は－1Cである。正しいのはどれか。

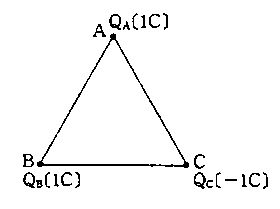
1: $Q_A$の受ける力の方向は線分BCに垂直である。

2: $Q_B$の受ける力の方向は線分CAに垂直である。

3: $Q_C$の受ける力の方向は線分ABに垂直である。

4: $Q_A$の受ける力の方向と$Q_B$の受ける力の方向とは同じである。

5: $Q_B$の受ける力の方向と$Q_C$の受ける力の方向とは同じである。

一様な電界に置かれた導体について正しいのはどれか。ただし、真空中とする。

a: 導体表面に電荷が現れる。

b: 導体内の電界の大きさは0となる。

c: 導体内の自由電子は電界の方向へ移動する。

d: 導体内では誘電分極が起こる。

e: 電界の方向は導体表面との接線方向となる。

1. a b　2. a e　3. b c　4. c d　5. d e

正しいのはどれか。

a: 作用する力とこれによって生じる反作用の力は大きさ、方向ともに同じである。

b: 合力が零であっても物体内部には力が存在することがある。

c: 丸棒の両端を同じ力で押すと棒の断面にはどこでも同じ圧縮力が生じる。

d: 丸棒の両端を同じ力で引っ張ると中央断面に生じる応力は零となる。

e: 丸棒の両端を押す力に差があっても棒は運動しない。

1. a b　2. a e　3. b c　4. c d　5. d e

電磁誘導の法則について正しいのはどれか。

a: 電荷が磁気を誘導することを表す。

b: ファラデーの法則ともいう。

c: コイルに磁石を出し入れするとコイルに起電力が発生することが説明される。

d: 直線電流の周りに磁界が発生することが説明される。

e: 磁石が鉄片を引き付けることが説明される。

1. a b　2. a e　3. b c　4. c d　5. d e

真空中に置かれた電荷、5μCと2μCとの間に0.01Nの力が働いた。電荷間の距離はどれか。ただし、1/(4πε0＝9×109 m/Fとする。(電気工学)　

1: 1m

2: 2m

3: 3m

4: 6m

5: 9m

N 巻きコイル（右巻き）をダイオード D、抵抗 R からなる回路につなぎ （図 1 ）、時間 t とともに変化する一様な磁界中に置いた。図 2 は、 3 つの時間領域 ①、②、③における B の時間変化を表している。 図 1 における電流 I の有無について正しいのはどれか。 ただし、ダイオードは理想的とする。

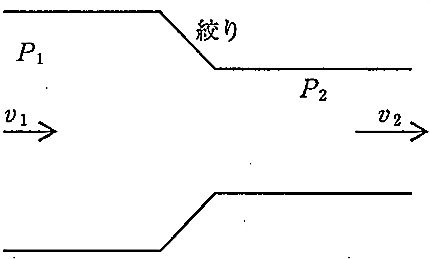
図のように水平に置かれた絞りのあるパイプに流体が流れている。絞りの前後の圧力差 P1 - P2 を表す式はどれか。ただし、流体の密度をρ、絞りの前の流速をV1、絞りの後の流速をV2とし、完全流体が定常流で流れているとする。

1: $ \frac {1}{2}\rho v^{2}_{1}$

2: $ \frac {1}{2}\rho v^{2}_{2}$

3: $ \frac {1}{2}\rho v_{1}v_{2}$

4: $ \frac {1}{2}\rho \left( v^{2}_{1}-v^{2}_{2}\right) $

5: $ \frac {1}{2}\rho \left( V^{2}_{2}-V^{2}_{1}\right) $

ダイオードの電流 I、電圧 E の方向を図 1 のように定めたとき、このダイ オードの特性グラフは図 2 のようになった。このとき、このダイオードの順方向電 圧 V F と逆方向降伏電圧 V R はどれか。

正しいのはどれか。

a: 金属に電界をかけると電界に比例するドリフト電流が流れる。

b: pn接合はオームの法則が成立する二端子の線形素子である。

c: 電子と正孔とが再結合するときはエネルギーを吸収する。

d: バイポーラトランジスタは電子または正孔の1種類のキャリアを利用するものである。

e: FETの特徴はゲート入力抵抗がきわめて高いことである。

1. a b　2. a e　3. b c　4. c d　5. d e

導体A、B、Cが図のように配置されている。導体Aに正電荷を付与するとき、正しいのはどれか。ただし、各導体間は絶縁されている。

a: 導体Cに静電誘導が生じる。

b: 導体C内に電界が生じる。

c: 導体Bの表面に負の電荷が誘起される。

d: 導体Cの電位が変化しても導体Bの電位は変化しない。

e: 導体Cを接地すると導体Bが静電シールドされる。

1. a b　2. a e　3. b c　4. c d　5. d e

図のような1回巻きのコイルの中心に向けて磁石を急速に動かした後、磁石を停止させた。このとき、コイルに流れる電流について正しいのはどれか。 

1: 磁石の動きに関わらず、電流は流れない。 

2: 磁石が動いている間、電流はA→B→Cの方向に流れる。 

3: 磁石が動いている間、電流はC→B→Aの方向に流れる。 

4: 磁石が停止すると、電流はA→B→Cの方向に流れる。 

5: 磁石が停止すると、電流はC→B→Aの方向に流れる。 

断面積Aの円柱状の棒を力Fで引っ張ると伸びるが、力を除くと元の状態に戻る。引張応力について正しいのはどれか。

1: Aに比例し、Fに反比例する。

2: Aに反比例し、Fに比例する。

3: AおよびFに比例する。

4: Fに比例し、Aには依存しない。

5: 棒の性質に依存する。

心電図の第Ⅰ、第Ⅱおよび第Ⅲ誘導の間には、Ⅱ＝Ⅰ＋Ⅲの関係が常に成立する。この関係式は次のどれから導かれるか。

1: ラプラスの式

2: フレミングの法則

3: キルヒホッフの法則

4: テブナンの定理

5: スターリングの法則

図のように+1クーロンの電荷と+4クーロンの電荷が一直線上に60cm離れて置かれている。この直線上に+1クーロンの電荷を置いたときにかかる力の総和が0となる位置はどれか。(電気工学)

1: A

2: B

3: C

4: D

5: E

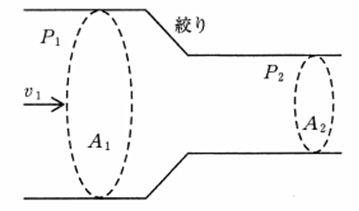
図のように水平に置かれた絞りのあるパイプに流体が流れている。絞りの前のパイプの断面積をA1、絞りの後のパイプの断面積をA2とする。絞りの前後の圧力差P1一P2を表す式はどれか。ただし、流体の密度をρ(一定)、絞りの前の流速をv1とし、完全流体が定常流で流れているとする。

1: $ \frac {1}{2}\rho v^{2}_{1}\left( \frac {A^{2}_{1}}{A^{2}_{2}}-1\right) $

2: $ \frac {1}{2}\rho v^{2}_{1}\left( 1-\frac {A^{2}_{1}}{A^{2}_{2}}\right) $

3: $ \frac {1}{2}\rho v^{2}_{1}\left( \frac {A_{1}}{A_{2}}-1\right) $

4: $ \frac {1}{2}\rho v^{2}_{1}\left( 1-\frac {A_{1}}{A_{2}}\right) $

5: $ \frac {1}{2}\rho v^{2}_{1}\left( \frac {A^{2}_{1}}{A^{2}_{2}}\right) $

+1C-1Cの点電荷の間に働く引力は、電荷間の距離が2×10^-2mのとき、1×10^-2mの場合に比べて何倍となるか。 

1: 2

2: 1

3: 1/2

4: 1/4

5: 1/8