第27回国試午後82問の類似問題

定常流の定義として正しいのはどれか。

1: ある断面を単位時間内に通過する流体の量が時間的に変化しない。

2: 流速がどこでも同じ値をとる。

3: 連続の方程式が成り立つ。

4: ずり速度がどこでも同じ値をとる。

5: 流線が時間的に変化しない。

粘性率$1×10^{-3}Pa・s$の粘性流体が内径1cmのまっすぐな円筒管内を流速10cm/sで流れている。これと相似な流れはどれか。ただし、流体の密度はすべて等しいとする。

1: 粘性率$1×10^{-3}Pa・s$,管内径2cm,流速20cm/s

2: 粘性率$1×10^{-3}Pa・s$,管内径0.5cm,流速5cm/s

3: 粘性率$2×10^{-3}Pa・s$,管内径0.5cm,流速10cm/s

4: 粘性率$2×10^{-3}Pa・s$,管内径1cm,流速20cm/s

5: 粘性率$2×10^{-3}Pa・s$,管内径2cm,流速20cm/s

血液の流れについて正しいのはどれか。

a: 流速は血管壁付近より中心付近の方が速い。

b: ずり速度(200/s以下)が小さいほど血液粘度は大きくなる。

c: ヘマトクリット値が高いほど血液粘度は小さくなる。

d: 血液はニュートン流体とみなせる。

e: 細い血管では心拍動に伴って乱流が生じる。

1. a b　2. a e　3. b c　4. c d　5. d e

非ニュートン流体について正しいのはどれか。

a: 密度が流速によって変化する。

b: 血液の非ニュートン性を決めているのは血漿である。

c: 流れる際に力学的エネルギーは消費されない。

d: 赤血球は血液の非ニュートン性に大きな影響を及ぼす。

e: キャッソンの式は血液の流れを表すのに適した実験式である。

1. a b　2. a e　3. b c　4. c d　5. d e

ある円筒管の両端に圧力差を与えて流体を流す場合と比べて、この円筒管の1/1000の断面積を持つ細い管を1000本並列にして同じ圧力差で流体を流す場合、流量は何倍になるか。ただし、太いほうの円筒管内の流れは層流とする。

1: 1

2: 1/10

3: 1/100

4: 1/1000

5: 1/10000

水平な円管内における流体の圧力で誤っているのはどれか。ただし、静水圧は0とし、外部とのエネルギーのやりとりはないものとする。（医用機械工学）

1: 流速が2倍になると動圧は2倍になる。

2: 流体の密度が2倍になると動圧は2倍になる。

3: 総圧は静圧と動圧との和になる。

4: 動圧が下がると静圧が上がる。

5: 流速を0にすると総圧は静圧に等しくなる。

円管内の流れのレイノルズ数を算出するのに必要な因子はどれか。

a: 粘性係数

b: 流 速

c: 管 径

d: 管路長

e: 拡散係数

1. a b c　2. a b e　3. a d e　4. b c d　5. c d e

流れにおけるベルヌーイの定理について正しいのはどれか。

a: 粘性流体に適用される。

b: 力学的エネルギーが保存される。

c: ひとつの流線上で成立する。

d: 重力とは無関係である。

e: レイノルズ数を導くことができる。

1. a b　2. a e　3. b c　4. c d　5. d e

図のように内径が変化する管内に理想流体が流れるときAB間の圧力差に比例するのはどれか。ただし、A、Bにおける流速を、とする。

1: $v_A$

2: $v_B$

3: $v_A-v_B$

4: $v_A^2$

5: $(v_A-v_B)^2$

内直径10mmの円管の中を動粘度4#10-6m2/sの流体が速度1m/sで流れているときのレイノルズ数はどれか。ただし、動粘度は、粘度/密度である。 

1: 40 

2: 250 

3: 400 

4: 2500 

5: 4000 

レイゾルズ数について誤っているのはどれか。

1: 流速に比例する。

2: 粘性率に反比例する。

3: 密度に比例する。

4: 層流から乱流に移行するときの値を臨界レイノルズ数という。

5: 臨界レイノルズ数は約100である。

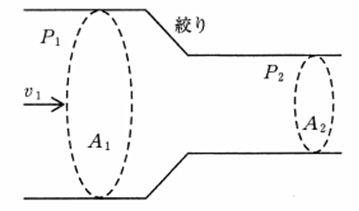
図のように水平に置かれた絞りのあるパイプに流体が流れている。絞りの前のパイプの断面積をA1、絞りの後のパイプの断面積をA2とする。絞りの前後の圧力差P1一P2を表す式はどれか。ただし、流体の密度をρ(一定)、絞りの前の流速をv1とし、完全流体が定常流で流れているとする。

1: $ \frac {1}{2}\rho v^{2}_{1}\left( \frac {A^{2}_{1}}{A^{2}_{2}}-1\right) $

2: $ \frac {1}{2}\rho v^{2}_{1}\left( 1-\frac {A^{2}_{1}}{A^{2}_{2}}\right) $

3: $ \frac {1}{2}\rho v^{2}_{1}\left( \frac {A_{1}}{A_{2}}-1\right) $

4: $ \frac {1}{2}\rho v^{2}_{1}\left( 1-\frac {A_{1}}{A_{2}}\right) $

5: $ \frac {1}{2}\rho v^{2}_{1}\left( \frac {A^{2}_{1}}{A^{2}_{2}}\right) $

粘性率4×10^-3Pa・Sの流体が内径3mmの直円管内を平均速度12 cm/Sで流れている。粘性率1×10^-3Pa･Sの流体を内径9mmの直円管内に流したときに、相似(レイノルズ数が同じ)になる平均速度[cm/S]はどれか。ただし、流体の密度はすべて等しいとする。

1: 0.25

2: 1

3: 9

4: 16

5: 144

内直径10mmの円管の中を動粘度4×10-6㎡/sの流体が速度1m/sで流れているときのレイノルズ数はどれか。ただし、動粘度は(粘度)／(密度)である。(医用機械工学)

1: 40

2: 250

3: 400

4: 2500

5: 4000

生体組織の力学的性質について誤っているのはどれか。

1: 血漿は非圧縮性流体である。

2: 大血管内の血液の流れは層流である。

3: 軟部組織のポアソン比はおよそ0.5である。

4: 軟部組織は硬組織に比べヤング率が小さい。

5: 筋のヤング率は直行方向より走行方向で大きい。

ある断面積をもつ1本の円筒管の両端に圧力差を与えて流体を流した。次に、はじめの1/10の断面積の円筒管を10本並列にし、同じ圧力差で流体を流した。そのときの流量は、はじめの状態の何倍になるか。ただし、管内の流れは層流とする。

1: 1/10

2: 1/√10

3: 1

4: √10

5: 10

流体の粘性について正しいのはどれか。

1: 温度に依存しない。

2: ヘマトクリット値が高くなると血液の粘性率は増加する。

3: 毛細血管を流れる血液はニュートン物体と見なせる。

4: 水は完全流体（理想流体）である。

5: 粘性率の単位はPa/sである。