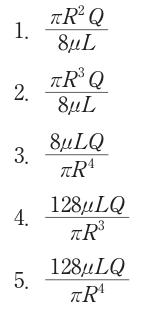第29回国試午後82問の類似問題
国試第22回午前:第82問
半径R、長さLの円管内を粘性率μの液体が流量Qで流れている。流れが定常な層流のとき、管の上流と下流の圧力差はどれか。
1: $ \frac {\pi R^{2}Q}{8\mu L}$
2: $ \frac {\pi R^{3}Q}{8\mu L}$
3: $ \frac {8\mu LQ}{\pi R^{4}}$
4: $ \frac {128\mu LQ}{\pi R^{3}}$
5: $ \frac {128\mu LQ}{\pi R^{4}}$
国試第31回午前:第83問
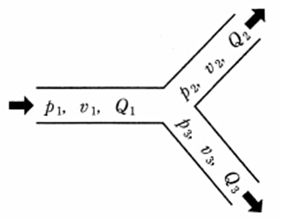
図のように1本の管から2本の管が分岐して内部に非圧縮性流体が流れて いるときに成り立つ式はどれか。ただし、pを圧力、vを流速、Qを流量とし、全ての管の断面積は等しいとする。
a: $ P_{1}=P_{2}+P_{3}$
b: $ v_{1}=v_{2}+v_{3}$
c: $ Q_{1}=Q_{2}+Q_{3}$
d: $ v^{2}_{1}=v^{2}_{2}+v^{2}_{3}$
e: $ Q^{2}_{1}=Q^{2}_{2}+Q^{2}_{3}$
1. a b 2. a e 3. b c 4. c d 5. d e
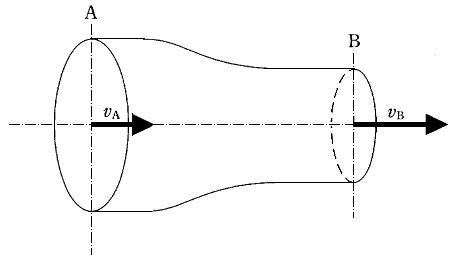
国試第30回午後:第82問
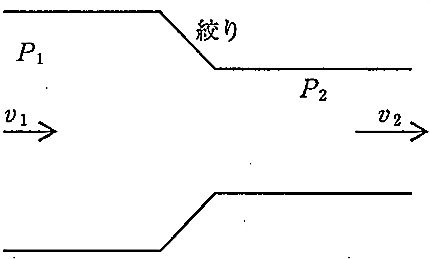
図のように水平に置かれた絞りのあるパイプに流体が流れている。絞りの前後の圧力差 P1 - P2 を表す式はどれか。ただし、流体の密度をρ、絞りの前の流速をV1、絞りの後の流速をV2とし、完全流体が定常流で流れているとする。
1: $ \frac {1}{2}\rho v^{2}_{1}$
2: $ \frac {1}{2}\rho v^{2}_{2}$
3: $ \frac {1}{2}\rho v_{1}v_{2}$
4: $ \frac {1}{2}\rho \left( v^{2}_{1}-v^{2}_{2}\right) $
5: $ \frac {1}{2}\rho \left( V^{2}_{2}-V^{2}_{1}\right) $
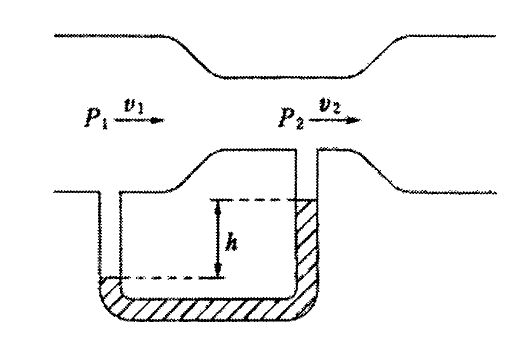
国試第31回午後:第82問
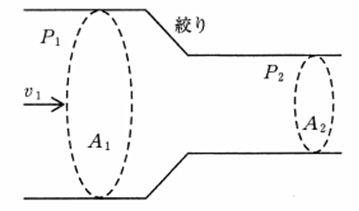
図のように水平に置かれた絞りのあるパイプに流体が流れている。絞りの前のパイプの断面積をA1、絞りの後のパイプの断面積をA2とする。絞りの前後の圧力差P1一P2を表す式はどれか。ただし、流体の密度をρ(一定)、絞りの前の流速をv1とし、完全流体が定常流で流れているとする。
1: $ \frac {1}{2}\rho v^{2}_{1}\left( \frac {A^{2}_{1}}{A^{2}_{2}}-1\right) $
2: $ \frac {1}{2}\rho v^{2}_{1}\left( 1-\frac {A^{2}_{1}}{A^{2}_{2}}\right) $
3: $ \frac {1}{2}\rho v^{2}_{1}\left( \frac {A_{1}}{A_{2}}-1\right) $
4: $ \frac {1}{2}\rho v^{2}_{1}\left( 1-\frac {A_{1}}{A_{2}}\right) $
5: $ \frac {1}{2}\rho v^{2}_{1}\left( \frac {A^{2}_{1}}{A^{2}_{2}}\right) $
国試第9回午後:第74問
粘性率$1×10^{-3}Pa・s$の粘性流体が内径1cmのまっすぐな円筒管内を流速10cm/sで流れている。これと相似な流れはどれか。ただし、流体の密度はすべて等しいとする。
1: 粘性率$1×10^{-3}Pa・s$,管内径2cm,流速20cm/s
2: 粘性率$1×10^{-3}Pa・s$,管内径0.5cm,流速5cm/s
3: 粘性率$2×10^{-3}Pa・s$,管内径0.5cm,流速10cm/s
4: 粘性率$2×10^{-3}Pa・s$,管内径1cm,流速20cm/s
5: 粘性率$2×10^{-3}Pa・s$,管内径2cm,流速20cm/s
国試第4回午前:第53問
流体の運動について正しいのはどれか。
a: 円管内の定常流では平均流速と円管断面積との積は場所によらず一定である。
b: 粘性率がずり速度によって変化する流体をニュートン流体という。
c: 臨界レイノルズ数を超えると粘性率はゼロとなる。
d: ベルヌーイの定理によれば動圧と静圧との和が流速に比例する。
e: 粘性率が零の完全流体では流体が流れても力学的エネルギーは消費されない。
1. a b 2. a e 3. b c 4. c d 5. d e