第1回国試午前56問の類似問題
国試第37回午前:第86問
ハーゲン・ポアズイユの式はどれか。ただし、Qを流量、ΔPを圧力差、rを管の半径、ηを粘性率、Lを管の長さとする。
1:$Q = \frac{\Delta P \cdot \mu \pi r^4}{8L}$
2:$Q = \frac{\Delta P \cdot \mu \pi r^2}{8L}$
3:$Q = \frac{\Delta P \cdot r^2}{8\mu \pi L}$
4:$Q = \frac{\Delta P \cdot \pi r^4}{8\mu L}$
5:$Q = \frac{\Delta P \cdot \pi r^2}{8\mu L}$
国試第19回午前:第57問
呼吸機能検査で正しいのはどれか。(生体計測装置学)
a:差圧式呼吸流量計はハーゲン・ポアズイユの式を利用する。
b:フライシュ型流量計は流路に細管を用いる。
c:ベネディクト・ロス型は熱線を用いて流量を測定する。
d:残気量はスパイロメータで測定する。
e:気道抵抗はスパイロメータで測定する。
1. a b 2. a e 3. b c 4. c d 5. d e
国試第3回午前:第70問
誤っているのはどれか。
1:大動脈中の流れは常に層流である。
2:レイノルズ数が約2,000を超えると層流から乱流へ変わる。
3:パアズイユの流れでは、流量は管径、管長、両端での圧力差に依存する。
4:生体組織は粘性と弾性をあわせもる。
5:生体組織の伸びの弾性はヤング率で表される。
国試第28回午後:第81問
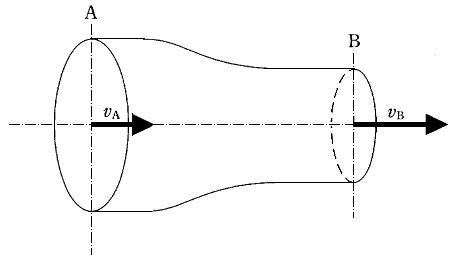
図のパイプ状の流路において、上流から下流に行くに従い断面積が半分になる流路がある。上流に対して下流での流速と管路抵抗について正しいのはどれか。ただし、管路内の水の流れは層流を維持しているものとする。
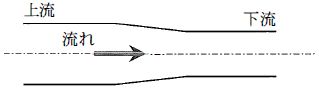
1:下流では流速は 1/2 倍になり、管路抵抗は 1/倍になる。
2:下流では流速は 1/2 倍になり、管路抵抗は 1/4 倍になる。
3:下流では流速は 1/2 倍になり、管路抵抗は 1/2 倍になる。
4:下流では流速は になり、管路抵抗は 2倍 になる。
5:下流では流速は になり、管路抵抗は 4倍 になる。
国試第29回午後:第82問
半径rの水平でまっすぐな円管内を粘性率nの液体が流れている。長さL離れた2点間の圧力差がΔPである場合、管内の流量Qを示す式はどれか。ただし、管内の流れは層流である。
1:$\frac {\pi r^{2}\mu \Delta P}{8L}$
2:$\frac {\pi r^{3}\Delta P}{8\mu L}$
3:$\frac {\pi r^{3}\mu \Delta P}{8L}$
4:$\frac {\pi r^{4}\Delta P}{8\mu L}$
5:$\frac {\pi r^{4}\mu \Delta P}{8L}$
国試第30回午後:第82問
図のように水平に置かれた絞りのあるパイプに流体が流れている。絞りの前後の圧力差 P1 - P2 を表す式はどれか。ただし、流体の密度をρ、絞りの前の流速をV1、絞りの後の流速をV2とし、完全流体が定常流で流れているとする。
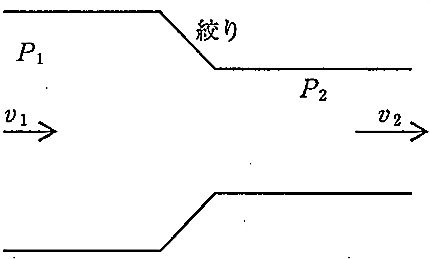
1:$ \frac {1}{2}\rho v^{2}_{1}$
2:$ \frac {1}{2}\rho v^{2}_{2}$
3:$ \frac {1}{2}\rho v_{1}v_{2}$
4:$ \frac {1}{2}\rho \left( v^{2}_{1}-v^{2}_{2}\right) $
5:$ \frac {1}{2}\rho \left( V^{2}_{2}-V^{2}_{1}\right) $