臨床工学技士問題表示
臨床工学技士国家試験
検索元問題
第21回 午後 第8問
10件の類似問題
図の回路のインピーダンスの絶対値はどれか。ただし、ωは角周波数である。...
広告
広告
48
臨床工学技士国家試験 -
第29回 午前
正答率:67%
類似度 50.2%
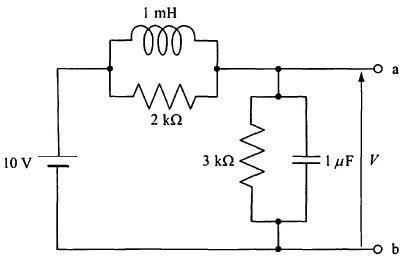
図の回路において、スイッチをa 側にして十分時間が経過した後、b 側に切換えた。正しいのはどれか。
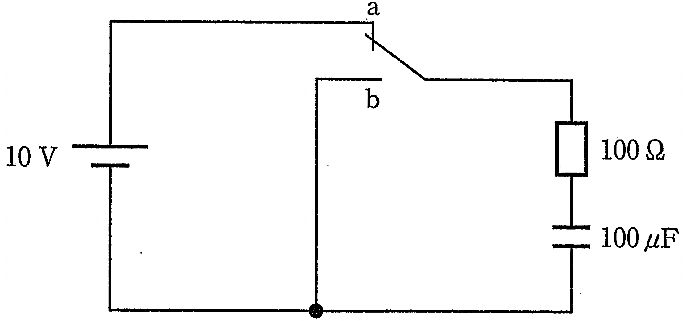
a
抵抗の最大電流値は100 mA である。
b
回路の時定数は0.1 s である。
c
コンデンサの両端電圧の最大値は5 V である。
d
コンデンサの両端電圧は指数関数的に増加する。
e
抵抗に流れる電流は指数関数的に減少する。
組み合わせ:
1. a b
2. a e
3. b c
4. c d
5. d e
35
臨床工学技士国家試験 -
第21回 午後
正答率:82%
類似度 50.0%
図のシステム伝達関数はどれか。
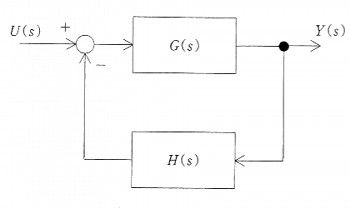
1
$\frac {1}{G\left( s\right) H\left( s\right) }$
2
$\frac {G\left( s\right) }{1-G\left( s\right) H\left( s\right) }$
3
$\frac {G\left( s\right) }{1+G\left( s\right) H\left( s\right) }$
4
$\frac {G\left( s\right) H\left( s\right) }{1-G\left( s\right) H\left( s\right) }$
5
$\frac {G\left( s\right) H\left( s\right) }{1+G\left( s\right) H\left( s\right) }$
広告