第35回国試午後53問の類似問題
国試第31回午後:第53問
図の回路の入力電圧Viと出力電圧V。の関係式(V。/Vi)はどれか。ただし、Aは理想演算増幅器とする。
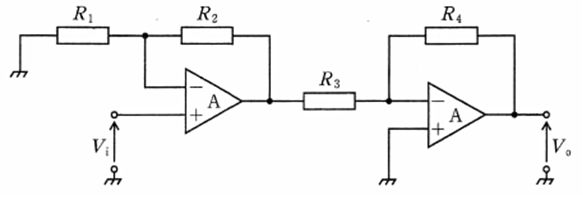
1: $ -\left( 1+\frac {R_{2}}{R_{1}}\right) \cdot \frac {R_{4}}{R_{3}}$
2: $ \left( 1+\frac {R_{2}}{R_{1}}\right) \cdot \frac {R_{4}}{R_{3}}$
3: $ -\left( 1+\frac {R_{2}}{R_{1}}\right) \cdot \left( 1+\frac {R_{4}}{R_{3}}\right) $
4: $ \frac {R_{2}}{R_{1}}\cdot \frac {R_{4}}{R_{3}}$
5: $ -\frac {R_{2}}{R_{1}}\cdot \left( 1+\frac {R_{4}}{R_{3}}\right) $
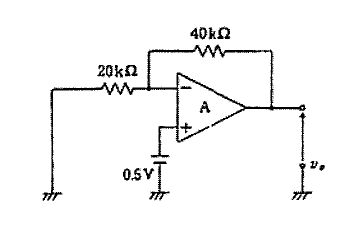
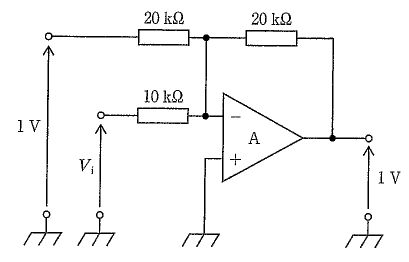
国試第18回午後:第17問
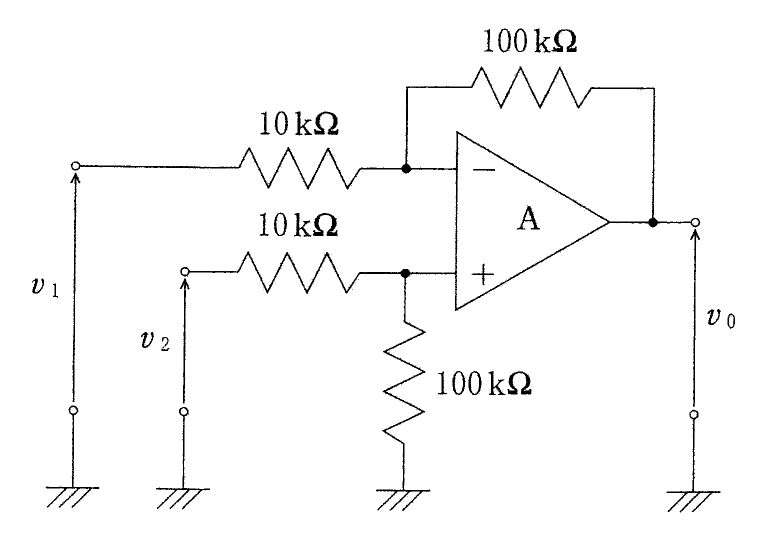
図の回路において二つの入力V1、V2とVoの関係を表す式はどれか。ただし、Aは理想演算増幅器とする。(電子工学)
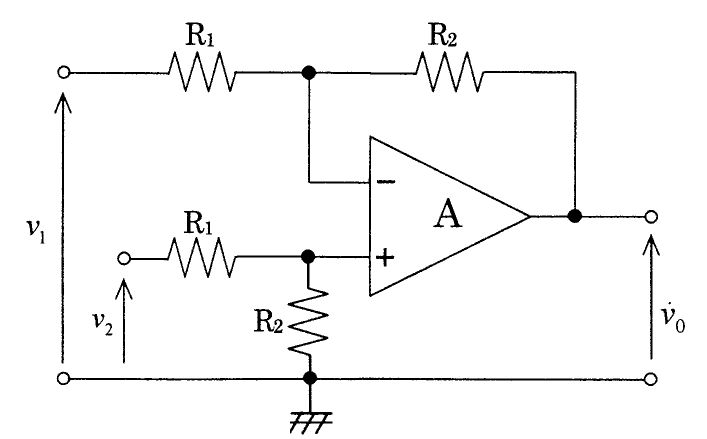
1: $V_{0}=\frac {R_{1}+R_{2}}{R_{1}}\left( V_{2}-V_{1}\right) $
2: $V_{0}=\frac {R_{1}+R_{2}}{R_{2}}\left( V_{2}-V_{1}\right) $
3: $V_{0}=\frac {R_{1}+R_{2}}{R_{2}-R_{1}}\left( V_{2}-V_{1}\right) $
4: $V_{0}=\frac {R_{1}}{R_{2}}\left( V_{2}-V_{1}\right) $
5: $V_{0}=\frac {R_{2}}{R_{1}}\left( V_{2}-V_{1}\right) $
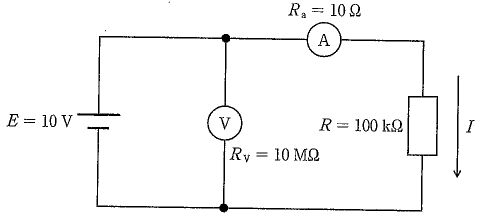
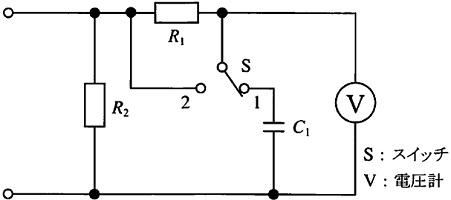
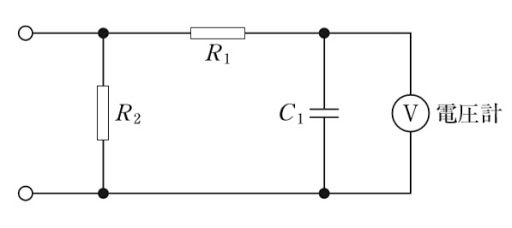
国試第21回午後:第8問
図の回路のインピーダンスの絶対値はどれか。ただし、ωは角周波数である。
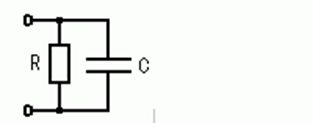
1: $ \sqrt {R+\frac {1}{\omega ^{2}c^{2}}}$
2: $ \sqrt {R^{2}+\omega ^{2}c^{2}}$
3: $ \frac {1}{\sqrt {R^{2}+\omega ^{2}c^{2}}}$
4: $ \sqrt {\frac {1}{1+\omega ^{2}c^{2}\pi ^{2}}}$
5: $\frac {1}{\sqrt {1+\omega ^{2}c^{2}R^{2}}}$
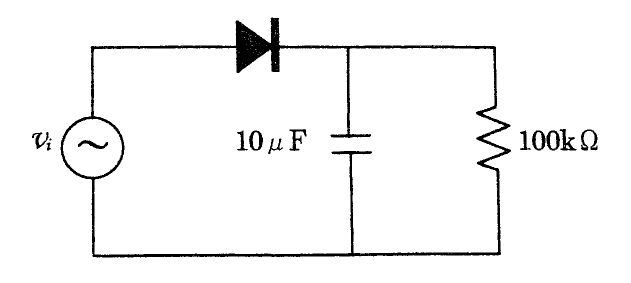
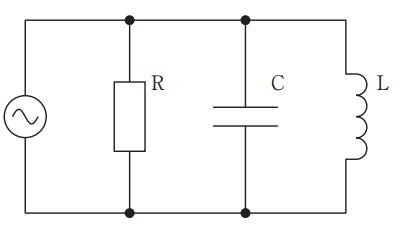
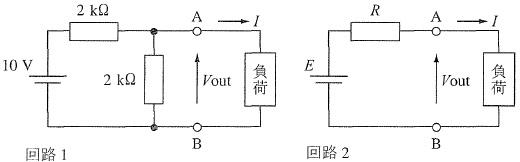
国試第12回午後:第8問
図のRCL回路に交流電圧を印加したとき正しいのはどれか。ただし、VR、VL及びVCはそれぞれR、L及びCで生じる電圧降下である。
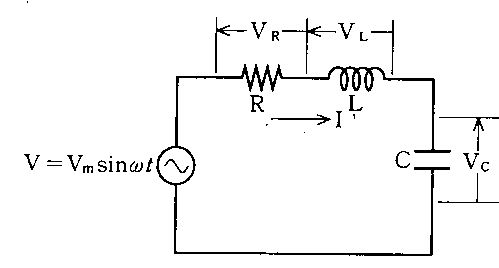
a: $ \omega L>\frac{1}{\omega C}$のとき電流Iの位相はVより遅れる。
b: $\frac{1}{\omega C}>\omega L$のとき回路は容量性を示す。
c: 共振時の角周波数ωは$\frac{1}{\sqrt{LC}}$で表される。
d: 共振時にはI=0である。
e: 共振時にはVL=0かつVC=0である。
1. a b c 2. a b e 3. a d e 4. b c d 5. c d e
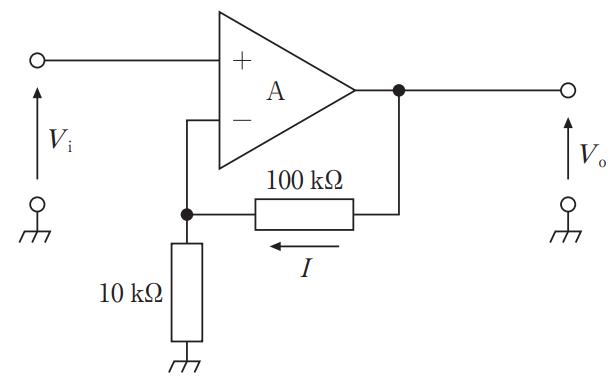
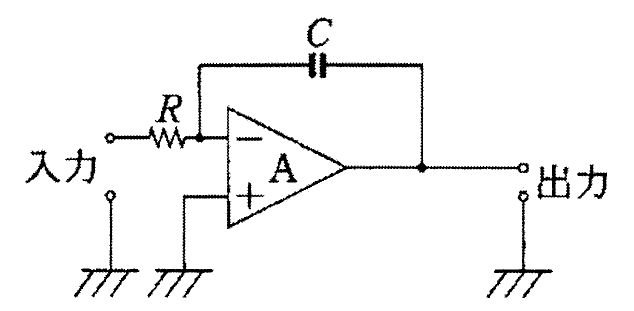
国試第22回午前:第55問
図の回路で入力Viと出力Voの関係を表す式はどれか。ただし、Aは理想演算増幅器とする。
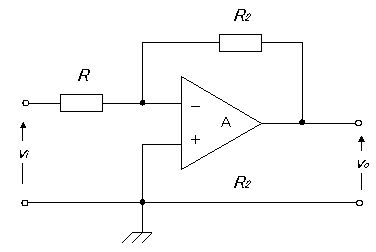
1: $ V_{0}=-\frac {1}{CR}\int V_{i}dt$
2: $ V_{0}=-CR\int V_{i}dt$
3: $ V_{0}=-\frac {R}{C}\int V_{i}dt$
4: $ V_{0}=-\frac {1}{CR}\frac {dV_{i}}{dt}$
5: $ V_{0}=-CR\frac {dV_{i}}{dt}$