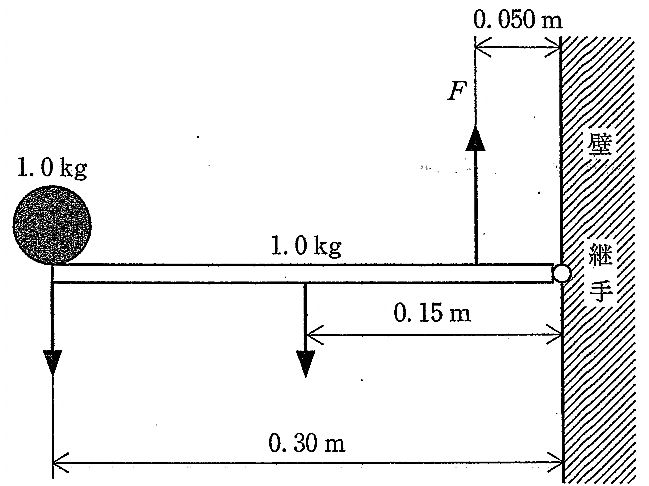
第5回国試午前49問の類似問題

正しいのはどれか。

1: 直線電流の近くでは、電流と平行に磁界が発生する。

2: 円形コイルに電流を流すと、コイル面内で中心に向かう磁界が発生する。

3: 一様な磁界中に棒磁石を磁界と直角に置くと、磁石は力を受けない。

4: 磁界中を磁界と直角方向に走行する電子は力を受けない。

5: 2本の平行導線に同方向に電流が流れていると、両者の間に力が働く。

真空中に1Cの電荷Aと-1Cの電荷Bが距離1m離れて存在する。正しいのはどれか。

1: AはBに引きつけられる向きに力を受ける。

2: Aの電荷を2倍にすればBの受ける力は4倍になる。

3: BはAに反発される向きに力を受ける。

4: AB間の中点での電気力線の方向はABを結ぶ線と垂直である。

5: AB間の距離を10cmにするとAの受ける力は100倍になる。

フックの法則について正しいのはどれか。

a: 塑性変形に対して成立する。

b: 応力はひずみに比例する。

c: 線形弾性変形に対して成立する。

d: 材料の体積が変わらないことを表す。

e: 材料の粘性を表す。

1. a b　2. a e　3. b c　4. c d　5. d e

真空中に 1 C（クーロン）の点電荷 A と 2 C の点電荷 B が 1 m の距離で存在する。正しいのはどれか。

1: B の受ける力は、A の受ける力の 2 倍である。

2: B の受ける力の方向は、A、B を結ぶ直線に垂直である。

3: A、B 間の距離を 0．5 m にすると、B の受ける力は 2 倍になる。

4: A の電荷量を 2 倍にすると、A 及び B の受ける力は 2 倍になる。

5: A 及び B の電荷量を両方とも 2 倍にしても、A の受ける力は変わらない。

正しいのはどれか。

1: 電界の強さは1Cの電荷に働く力によって定義される。

2: 単一電荷によって生じる電界の強さは電荷からの距離に反比例する。

3: 単一電荷によって生じる電位は電荷からの距離の2乗に反比例する。

4: 電位は1Cの電荷を動かすのに要する力である。

5: 電位はベクトル量である。

正しいのはどれか。

a: 等速円運動をしている物体には接線力が作用している。

b: 角速度とは単位時間当たりに回転する角度のことである。

c: 物体を回転させようとする働きのことをモーメントという。

d: モーメントは力と長さとの積で表される。

e: モーメントは慣性モーメントと角速度との積に等しい。

1. a b c　2. a b e　3. a d e　4. b c d　5. c d e

質量1.0 kg の剛体の棒が自由に回る継手を介して壁に取り付けられている。継手から0.30 m の所に質量1.0 kg の物体を置いた。棒が水平で動かないとき、継手から0.050 m の所に取り付けたひもが鉛直方向に引っ張るおよその力F［N］はどれか。ただし、棒の重心の位置は継手から0.15 m の所である。

1: 2

2: 5

3: 10

4: 20

5: 88

ステンレス鋼に張力を与えて破断するまでの応力ーひずみの関係について正しいのはどれか。

1: 応力を取り去れば変形が残らない最大限度を比例限度という。

2: ひずみが応力に比例して増加する最大限度を弾性限度という。

3: 降伏点より先では応力が増加するとひずみは著しく増大する。

4: 破壊点では張力が最大になる。

5: ひずみが最大となるときに応力は最大となる。

物体に働く応力とひずみについて誤っているのはどれか。

1: 応力はベクトルで表される。

2: 応力の単位は［Pa］である。

3: ひずみの単位は［m］である。

4: 弾性率は応力とひずみの比である。

5: 弾性率の単位は［Pa］である。

真空中に－2C（クーロン）の電荷Aと－1Cの電荷Bが距離1ｍ離れて存在する。

a: AはBに引きつけられる向きに力を受ける。

b: Aの受ける力はBの受ける力は2倍になる。

c: BはAに反発される向きに力を受ける。

d: A、B間の距離を10mにするとAの受ける力は1/100になる。

e: A、B間の距離を50cmにするとBの受ける力は2倍になる。

1. a b　2. a e　3. b c　4. c d　5. d e

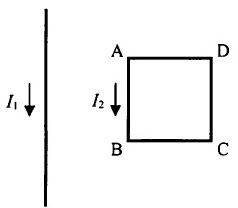
図のように真空中で、r離れた無限に長い平行導線1、2に、大きさが等しい電流I1、I2が同じ方向に流れているとき、正しいのはどれか。ただし、I1が導線2につくる磁束密度をB1、I2が導線1につくる磁束密度をB2、導線2の単位長さにかかる力をF2とする。

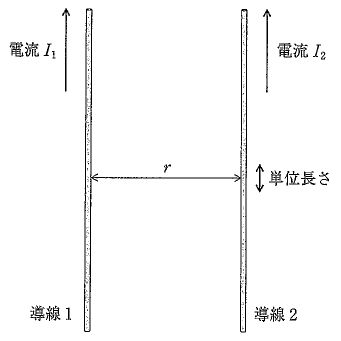
1: 磁束密度B1電流I1に反比例する。

2: 電流I1と磁束密度B1との向きは逆方向となる。

3: 導線1導線2の間には引力が働く。

4: 力F2は導線間の距離rに比例する。

5: 磁束密度B1と磁束密度B2の向きは同方向となる。

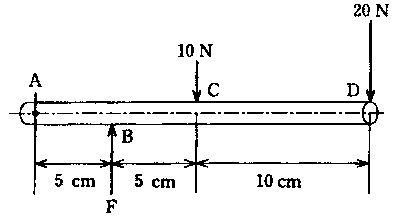
図の物体の上面（abfe）に外力Fを加えたところ、点線のようにせん断（ずり）変形した。正しいのはどれか。

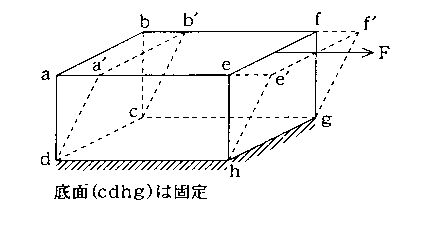
a: 面cdhgに作用する応力をせん断応力という。

b: せん断ひずみは$\frac{aa'}{ad}$で表される。

c: せん断応力はせん断ひずみに比例する。

d: Fを面adheの面積で割った値を垂直応力という。

e: Fを面abcdの面積で割った値をヤング率という。

1. a b c　2. a b e　3. a d e　4. b c d　5. c d e

正しいのはどれか。

a: 力をF、質量をm、加速度をαとするとF=m/αとなる。

b: 力の単位はPaである。

c: 力の3つの要素は、大きさ、方向、作用点である。

d: 大きさと方向を待った量をベクトルという。

e: 速度はスカラーである。

1. a b　2. a e　3. b c　4. c d　5. d e

同一平面内に長い直線導線と正方形の閉回路ABCDがあり（辺ABは直線導線と平行）、それぞれ図の向きに電流I1とI2が流れている。このとき閉回路に働く力として正しいのはどれか。

1: 紙面左向きの力が働く。

2: 紙面右向きの力が働く。

3: 紙面下向きの力が働く。

4: 紙面上向きの力が働く。

5: 紙面手前に向かう力が働く。

力学的な波動について正しいのはどれか。

a: 横波と縦波の2種類がある。

b: 同じ性質の二つの波が重なるとき位相の差により干渉の様子が異なる。

c: 弾性体中を進む横波の速度と縦波の速度とは等しい。

d: 弾性体中を進む波の速度は弾性率によらず常に一定である。

e: 弦を伝わる横波の速度は張力を増すと遅くなる。

1. a b　2. a e　3. b c　4. c d　5. d e

真空中に2Cの電荷Aと-1Cの電荷Ｂが距離1m離れて存在する。正しいのはどれか。

a: AはBに引き付けられる向きに力を受ける。

b: Aの受ける力はBの受ける力の2倍である。

c: BはAに反発される向きに力を受ける。

d: AB間の距離を10mにするとAの受ける力は1/10になる。

e: AB間の距離を50cmにするとBの受ける力は4倍になる。

1. a b　2. a e　3. b c　4. c d　5. d e

丸棒がA点でピン支持されている。棒のC、D点にそれぞれ下向きに10N、20Nの力が加わっているとき、棒を水平に保持するためにB点に上向きに加える力Fはどれか。ただし、丸棒の重さは無視できる。

1: 50N

2: 100N

3: 200N

4: 300N

5: 500N

物体の変形について誤っているのはどれか。

a: 荷重を除いたときに完全に元の形に戻る性質を弾性と呼ぶ。

b: 弾性限度内では荷重は変形量に比例する。

c: 弾性限度内の応力のひずみに対する比をフック率と呼ぶ。

d: 縦弾性係数が大きいほど体積弾性係数は小さい。

e: 弾性限度を超える荷重を加えると塑性変形を生じる。

1. a b　2. a e　3. b c　4. c d　5. d e

質量が無視できる直角三角形の板が、図のように頂点Aを中心として抵抗なく回転可能である。頂点Cには辺BCと平行な方向に10 Nの力が作用している。板が回転しないために頂点Bに加える力はどれか。　ただし、x軸は辺AC、y軸は辺ABに平行とし、矢印方向を正とする。（医用機械工学）

1: x軸の正方向に6N

2: x軸の負方向に6N

3: x軸の負方向に8N

4: y軸の正方向に6N

5: y軸の負方向に8N

水平な円管内における流体の圧力で誤っているのはどれか。ただし、静水圧は0とし、外部とのエネルギーのやりとりはないものとする。（医用機械工学）

1: 流速が2倍になると動圧は2倍になる。

2: 流体の密度が2倍になると動圧は2倍になる。

3: 総圧は静圧と動圧との和になる。

4: 動圧が下がると静圧が上がる。

5: 流速を0にすると総圧は静圧に等しくなる。