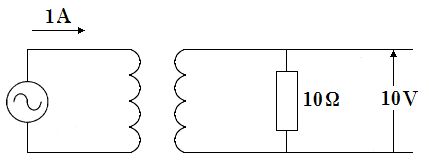
第19回国試午後7問の類似問題
国試第12回午後:第8問
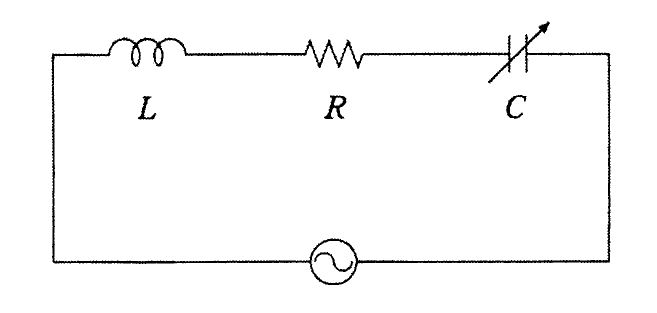
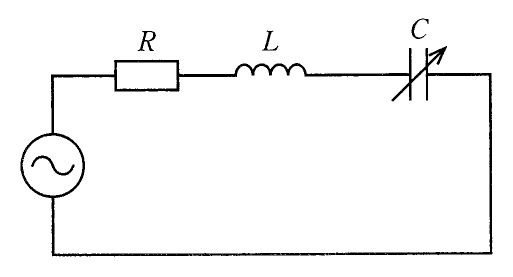
図のRCL回路に交流電圧を印加したとき正しいのはどれか。ただし、VR、VL及びVCはそれぞれR、L及びCで生じる電圧降下である。
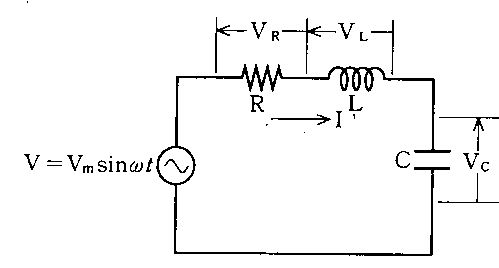
a: $ \omega L>\frac{1}{\omega C}$のとき電流Iの位相はVより遅れる。
b: $\frac{1}{\omega C}>\omega L$のとき回路は容量性を示す。
c: 共振時の角周波数ωは$\frac{1}{\sqrt{LC}}$で表される。
d: 共振時にはI=0である。
e: 共振時にはVL=0かつVC=0である。
1. a b c 2. a b e 3. a d e 4. b c d 5. c d e
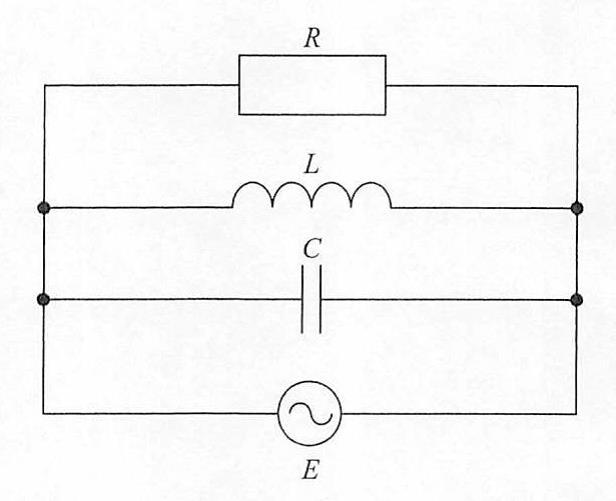
国試第23回午後:第48問
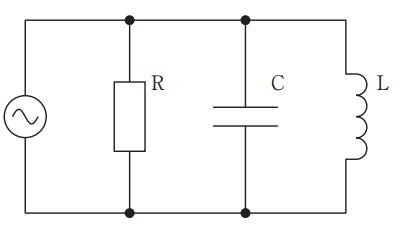
図のRC並列回路のインピーダンスの大きさはどれか。ただし、ωは角周波数である。
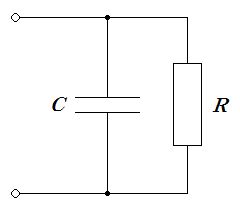
1: $\frac{R}{\sqrt{1+\omega^2C^2R^2}}$
2: $ R\sqrt{1+\omega^2C^2R^2}$
3: $\frac{1}{\omega C\sqrt{1+\omega^2C^2R^2}}$
4: $\frac{\sqrt{1+\omega^2C^2R^2}}{\omega C}$
5: $\frac{R}{\omega C}\sqrt{1+\omega^2C^2R^2}$
国試第22回午前:第50問
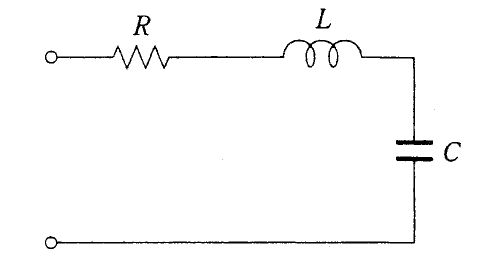
RLC直列回路に交流電圧を印加したときの印加電圧に対する電流の位相角θはどれか。ただし、ωは角周波数である。
1: $ \tan ^{-1}\left( \frac {L}{\omega CR}\right) $
2: $ \tan ^{-1}\left( \frac {R}{\omega CR}\right) $
3: $ \tan ^{-1}\left( \frac {R}{\frac {1}{\omega C}-\omega L}\right) $
4: $\tan ^{-1}\left( \frac {\frac {1}{\omega C}-\omega L}{R}\right)$
5: $ \tan ^{-1}\left( \frac {\omega L}{1+\omega CR}\right) $
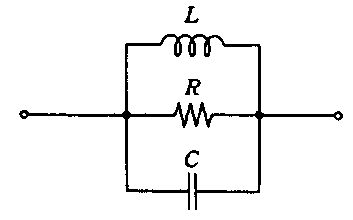
国試第25回午後:第49問
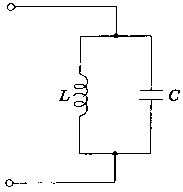
図の回路のインピーダンスの大きさはどれか。ただし、ωは角周波数とする。
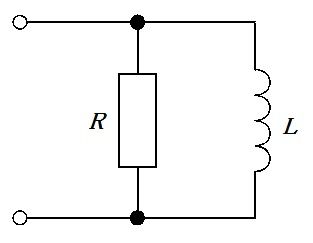
1: $ \sqrt {R^{2}+\omega ^{2}L^{2}}$
2: $ \frac {\omega RL}{R+\omega L}$
3: $ \frac {\omega RL}{\sqrt {R^{2}+\omega ^{2}L^{2}}}$
4: $ \frac {R}{\sqrt {R^{2}+\omega ^{2}L^{2}}}$
5: $ \frac {\omega L}{\sqrt {R^{2}+\omega ^{2}L^{2}}}$