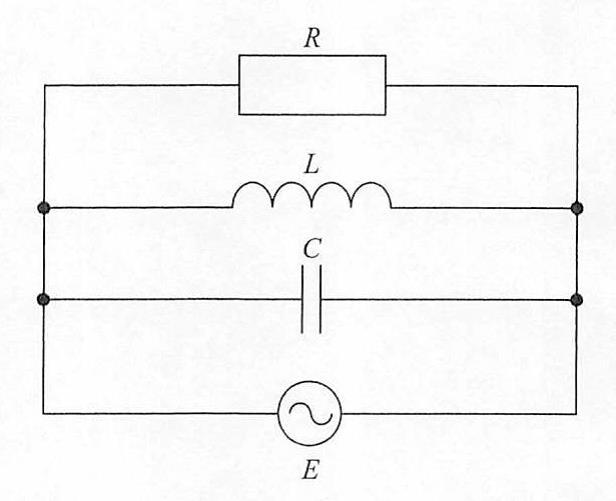
第9回国試午後12問の類似問題

抵抗R、インダクタLの直列回路において正しいのはどれか。（電気工学）

1: 周波数が高くなるほど回路電流は増加する。

2: 共振周波数が存在する。

3: Rの電流とLの電流の比は周波数に比例する。

4: 回路電流は電源電圧より位相がπ/2進んでいる。

5: Lの端子電圧はRの端子電圧より位相がπ/2進んでいる。

図の回路について誤っているのはどれか。

a: 正弦波電流に対するLとCそれぞれの両端の電圧は同相である。

b: 直流ではインピーダンスが無限大である。

c: 共振するとインピーダンスは抵抗Rとなる。

d: 共振周波数は1/(2π√LC)である。

e: 共振周波数以上の高い周波数ではインピーダンスは0に近づく。

1. a b　2. a e　3. b c　4. c d　5. d e

図の回路において、インダクタンスL、抵抗Rは一定であり、キャパシタンスCは可変である。共振周波数を2倍にするためには、Cをもとの何倍にすればよいか。（電気工学）

1: $\frac{1}{4}$

2: $\frac{1}{2}$

3: $\frac{1}{\sqrt2}$

4: $\sqrt2$

5: 2

抵抗R、インダクタL、キャパシタCからなる直列共振回路がある。R、Lを一定とした場合、共振周波数を2倍にするにはCの値を何倍にすればよいか。

1: 1/4

2: 1/2

3: √2

4: 2

5: 4

図の回路が共振状態にあるとき正しいのはどれか。 

1: Rの抵抗値を２倍にすると、回路の全インピーダンスは４倍になる

2: Cの静電容量を2倍にすると、回路の全インピーダンスは1/2倍になる

3: Lのインダクタンスを2倍にすると、回路のアドミタンスは1/4倍になる

4: Cの静電容量を4倍にすると、共振周波数は1/2倍になる

5: Rの抵抗値を4倍にすると共振周波数は2倍になる

図の回路について誤っているのはどれか。

1: 正弦波電流ではコイルLとコンデンサCとに流れる電流は同位相である。

2: 直流ではインピーダンスが0となる。

3: 共振するとインビーダンスは無限大となる。

4: 共振周波数より十分大きい周波数ではインピーダンスが0に近づく。

5: 共振周波数は$\frac{1}{2\pi\sqrt{LC}}$である。

図の回路について、正しいのはどれか。ただし、Aは理想演算増幅器とする。

a: 遮断周波数より十分に低い帯域で微分特性を有する。

b: コンデンサC1と抵抗R2に流れる電流は等しい。

c: 遮断周波数は314Hzである。

d: 直流成分は通過する。

e: 入力インピーダンスは抵抗R1とR2で決まる。

1. a b　2. a e　3. b c　4. c d　5. d e

図のように、インダクタンスLと抵抗Rが接続された回路に正弦波電圧v=Esinωtを印加したときに流れる電流をiとする。正しいのはどれか。

1: L、R、ωに無関係にiはvと同位相である。

2: L、R、ωに無関係にiはvよりπ/2位相が進む。

3: L、R、ωに無関係にiはvよりπ/2位相が遅れる。

4: iはvより位相が進んでいるがその値は0以上π/2以下である。

5: iはvより位相が遅れているがその値は0以上π/2以下である。

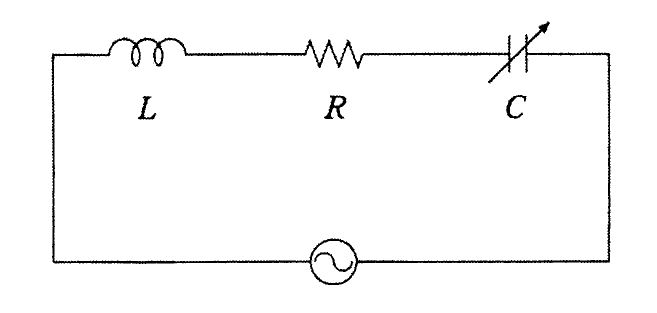
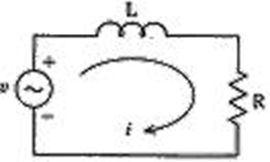
図に示す直列共振回路について正しいのはどれか。

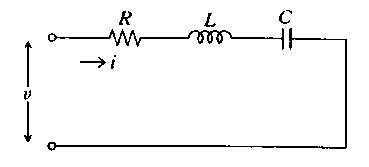
a: 電圧vの周波数が共振周波数に等しいとき電圧vと電流iの位相は等しい。

b: 電圧vの周波数が共振周波数より極めて低いと電流iは0に近い。

c: 共振周波数におけるインピーダンスはRになる。

d: インピーダンスは共振周波数において最も大きくなる。

e: 電圧vの周波数が共振周波数より極めて高いとコンデンサにかかる電圧は高い。

1. a b c　2. a b e　3. a d e　4. b c d　5. c d e

図の回路について正しいのはどれか。

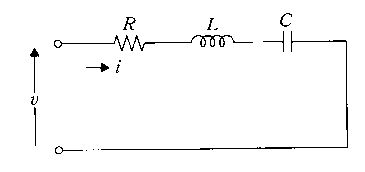
a: 電圧vの周波数が共振周波数に等しいとき、電圧vと電流iの位相は等しい。

b: 電圧vの周波数が共振周波数より極めて低いと電流iは0に近い。

c: 共振周波数におけるインピーダンスはRなる。

d: インピーダンスは共振周波数において最も大きくなる。

e: 電圧vの周波数が共振周波数より極めて高いとコンデンサにかかる電圧は高い。

1. a b c　2. a b e　3. a d e　4. b c d　5. c d e

交流回路で正しいのはどれか。

1: インダクタンスLは電圧に対して電流の位相を90°進ませる作用がある。

2: 容量Cのリアクタンスの大きさは周波数に比例する。

3: 電流の流れにくさはインピーダンスによって表現される。

4: 電流の流れやすさはリアクタンスによって表現される。

5: 平均電力は電圧実効値と電流実効値とをかけたものに常に等しい。

RLC直列回路において共振時の電気インピーダンスの大きさはどれか。ただし、ωは角周波数とする。

1: R

2: 1/(ωC)

3: ωL+1/(ωC)

4: $ \sqrt {R^{2}+\left( \omega L\right) ^{2}}$

5: (L/C)1/2

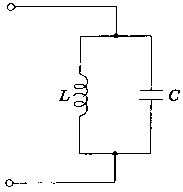
図の回路のインピーダンスの大きさはどれか。ただし、ωは角周波数とする。

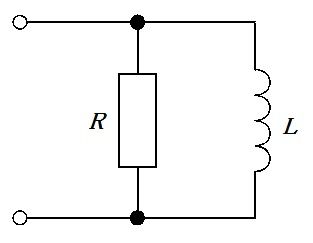
1: $ \sqrt {R^{2}+\omega ^{2}L^{2}}$

2: $ \frac {\omega RL}{R+\omega L}$

3: $ \frac {\omega RL}{\sqrt {R^{2}+\omega ^{2}L^{2}}}$

4: $ \frac {R}{\sqrt {R^{2}+\omega ^{2}L^{2}}}$

5: $ \frac {\omega L}{\sqrt {R^{2}+\omega ^{2}L^{2}}}$

図のような CR 直列回路に連続した方形波を入力させたときについて正しいのはどれか。

1: 抵抗の両端電圧 vR は積分波形を示す。

2: 回路の時定数は 0．47 ns である。

3: パルス幅に対して時定数は十分小さい。

4: vi~= R・i と表すことができる。

5: キャパシタの両端電圧 vC の波形はほぼ三角波となる。

抵抗R、容量C、インダクタンスLの3つの素子が並列に接続されている。この回路に交流電源を接続すると各素子にそれぞれ実効値1Aの電流が流れる。交流電源から流れ出ている電流の実効値（A）として正しいのはどれか。

1: 3

2: 2

3: 1.5

4: 1

5: 0.5

図の回路について、正しいのはどれか。ただし、Aは理想演算増幅器とする。

a: 時定数は20 msである。

b: 通過域での増幅度は20 である。

c: 直流成分はカットされる。

d: コンデンサC1と抵抗R2に流れる電流は等しい。

e: 入力インピーダンスは抵抗R1とR2で決まる。

1. a b　2. a e　3. b c　4. c d　5. d e

RLC直列回路において共振時の電気インピーダンスの大きさはどれか。ただし、ωは共振角周波数とする。

1: $R$

2: $ \frac {1}{\omega C}$

3: $ \omega L$

4: $ \omega L+\frac {1}{\omega C}$

5: $ \frac {1}{\sqrt {LC}}$

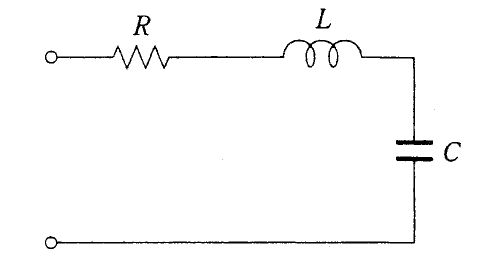
図の回路のインピーダンスの絶対値はどれか。ただし、ωは角周波数である。

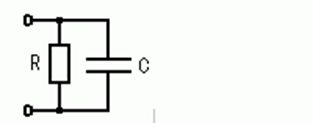
1: $ \sqrt {R+\frac {1}{\omega ^{2}c^{2}}}$

2: $ \sqrt {R^{2}+\omega ^{2}c^{2}}$

3: $ \frac {1}{\sqrt {R^{2}+\omega ^{2}c^{2}}}$

4: $ \sqrt {\frac {1}{1+\omega ^{2}c^{2}\pi ^{2}}}$

5: $\frac {1}{\sqrt {1+\omega ^{2}c^{2}R^{2}}}$

図の回路が共振状態にあるとき、抵抗器に流れる電流は何Aか。ただし、R=200Ω、L=1.6mH、C=100μF、E=100V（実効値）とする。

1: 0.5

2: 1.0

3: 1.5

4: 2.0

5: 5.0

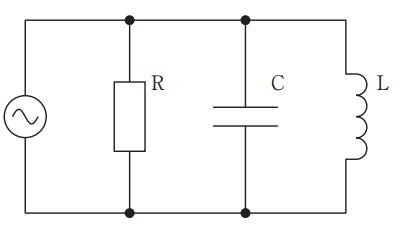
図のRC並列回路のインピーダンスの大きさはどれか。ただし、ωは角周波数である。

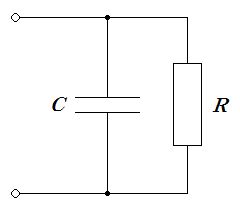
1: $\frac{R}{\sqrt{1+\omega^2C^2R^2}}$

2: $ R\sqrt{1+\omega^2C^2R^2}$

3: $\frac{1}{\omega C\sqrt{1+\omega^2C^2R^2}}$

4: $\frac{\sqrt{1+\omega^2C^2R^2}}{\omega C}$

5: $\frac{R}{\omega C}\sqrt{1+\omega^2C^2R^2}$