臨床工学技士問題表示
臨床工学技士国家試験
検索元問題
第26回 午後 第51問
17件の類似問題
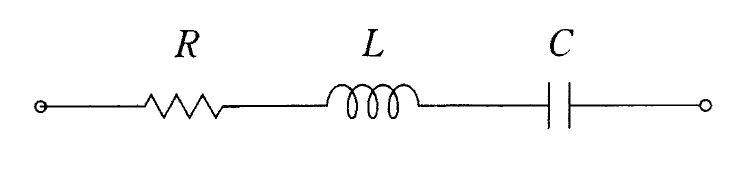
RLC直列回路において共振時の電気インピーダンスの大きさはどれか。ただし、ωは角周波数とする。...
広告
49
臨床工学技士国家試験 -
第32回 午後
重要度:低
正答率:77%
類似度 91.9%
RLC直列回路において共振時の電気インピーダンスの大きさはどれか。ただし、ωは共振角周波数とする。
1
$R$
2
$ \frac {1}{\omega C}$
3
$ \omega L$
4
$ \omega L+\frac {1}{\omega C}$
5
$ \frac {1}{\sqrt {LC}}$
48
臨床工学技士国家試験 -
第23回 午後
類似度 76.8%
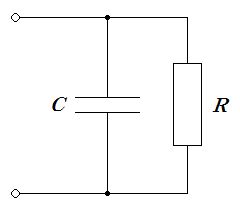
図のRC並列回路のインピーダンスの大きさはどれか。ただし、ωは角周波数である。
1
$\frac{R}{\sqrt{1+\omega^2C^2R^2}}$
2
$ R\sqrt{1+\omega^2C^2R^2}$
3
$\frac{1}{\omega C\sqrt{1+\omega^2C^2R^2}}$
4
$\frac{\sqrt{1+\omega^2C^2R^2}}{\omega C}$
5
$\frac{R}{\omega C}\sqrt{1+\omega^2C^2R^2}$
49
臨床工学技士国家試験 -
第25回 午後
正答率:47%
類似度 73.4%
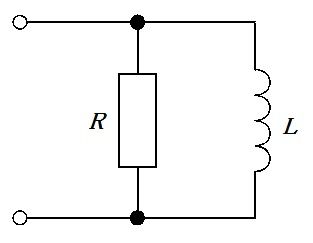
図の回路のインピーダンスの大きさはどれか。ただし、ωは角周波数とする。
1
$ \sqrt {R^{2}+\omega ^{2}L^{2}}$
2
$ \frac {\omega RL}{R+\omega L}$
3
$ \frac {\omega RL}{\sqrt {R^{2}+\omega ^{2}L^{2}}}$
4
$ \frac {R}{\sqrt {R^{2}+\omega ^{2}L^{2}}}$
5
$ \frac {\omega L}{\sqrt {R^{2}+\omega ^{2}L^{2}}}$
8
臨床工学技士国家試験 -
第21回 午後
類似度 71.0%
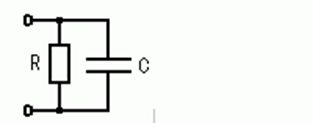
図の回路のインピーダンスの絶対値はどれか。ただし、ωは角周波数である。
1
$ \sqrt {R+\frac {1}{\omega ^{2}c^{2}}}$
2
$ \sqrt {R^{2}+\omega ^{2}c^{2}}$
3
$ \frac {1}{\sqrt {R^{2}+\omega ^{2}c^{2}}}$
4
$ \sqrt {\frac {1}{1+\omega ^{2}c^{2}\pi ^{2}}}$
5
$\frac {1}{\sqrt {1+\omega ^{2}c^{2}R^{2}}}$
9
臨床工学技士国家試験 -
第15回 午後
類似度 65.2%
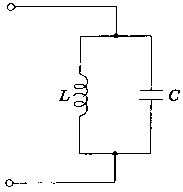
図の回路について誤っているのはどれか。
1
正弦波電流ではコイルLとコンデンサCとに流れる電流は同位相である。
2
直流ではインピーダンスが0となる。
3
共振するとインビーダンスは無限大となる。
4
共振周波数より十分大きい周波数ではインピーダンスが0に近づく。
5
共振周波数は$\frac{1}{2\pi\sqrt{LC}}$である。
広告
50
臨床工学技士国家試験 -
第22回 午前
正答率:42%
類似度 64.7%
RLC直列回路に交流電圧を印加したときの印加電圧に対する電流の位相角θはどれか。ただし、ωは角周波数である。
1
$ \tan ^{-1}\left( \frac {L}{\omega CR}\right) $
2
$ \tan ^{-1}\left( \frac {R}{\omega CR}\right) $
3
$ \tan ^{-1}\left( \frac {R}{\frac {1}{\omega C}-\omega L}\right) $
4
$\tan ^{-1}\left( \frac {\frac {1}{\omega C}-\omega L}{R}\right)$
5
$ \tan ^{-1}\left( \frac {\omega L}{1+\omega CR}\right) $
10
臨床工学技士国家試験 -
第17回 午後
正答率:70%
類似度 63.7%
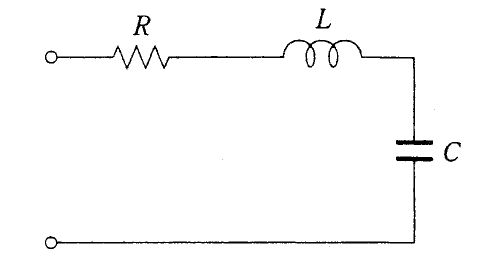
図の回路について誤っているのはどれか。
a
正弦波電流に対するLとCそれぞれの両端の電圧は同相である。
b
直流ではインピーダンスが無限大である。
c
共振するとインピーダンスは抵抗Rとなる。
d
共振周波数は1/(2π√LC)である。
e
共振周波数以上の高い周波数ではインピーダンスは0に近づく。
組み合わせ:
1. a b
2. a e
3. b c
4. c d
5. d e
12
臨床工学技士国家試験 -
第9回 午後
類似度 63.6%
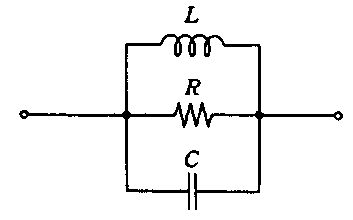
図のようなインダクダンスL〔H〕、キャパシタンスC〔F〕、抵抗R〔Ω〕の並列回路について正しいのはどれか。
1
十分高い周波数ではLのみで近似できる。
2
十分低い周波数ではCのみで近似できる。
3
共振周波数でのインピーダンスはR〔Ω〕である。
4
アドミタンスの絶対値の最大は1/R〔S〕である。
5
直流での抵抗はR〔Ω〕である。
10
臨床工学技士国家試験 -
第13回 午後
正答率:47%
類似度 63.4%
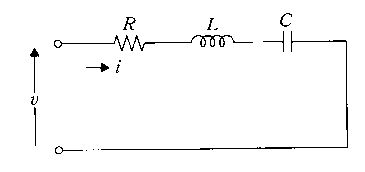
図の回路について正しいのはどれか。
a
電圧vの周波数が共振周波数に等しいとき、電圧vと電流iの位相は等しい。
b
電圧vの周波数が共振周波数より極めて低いと電流iは0に近い。
c
共振周波数におけるインピーダンスはRなる。
d
インピーダンスは共振周波数において最も大きくなる。
e
電圧vの周波数が共振周波数より極めて高いとコンデンサにかかる電圧は高い。
組み合わせ:
1. a b c
2. a b e
3. a d e
4. b c d
5. c d e
広告
10
臨床工学技士国家試験 -
第10回 午後
正答率:55%
類似度 63.0%
図に示す直列共振回路について正しいのはどれか。
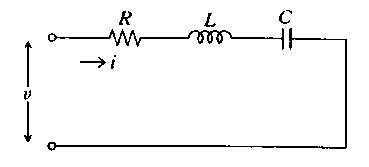
a
電圧vの周波数が共振周波数に等しいとき電圧vと電流iの位相は等しい。
b
電圧vの周波数が共振周波数より極めて低いと電流iは0に近い。
c
共振周波数におけるインピーダンスはRになる。
d
インピーダンスは共振周波数において最も大きくなる。
e
電圧vの周波数が共振周波数より極めて高いとコンデンサにかかる電圧は高い。
組み合わせ:
1. a b c
2. a b e
3. a d e
4. b c d
5. c d e
8
臨床工学技士国家試験 -
第12回 午後
類似度 62.2%
図のRCL回路に交流電圧を印加したとき正しいのはどれか。ただし、VR、VL及びVCはそれぞれR、L及びCで生じる電圧降下である。
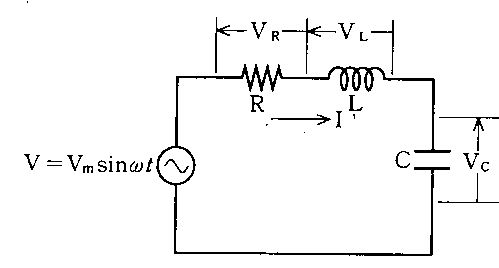
a
$ \omega L>\frac{1}{\omega C}$のとき電流Iの位相はVより遅れる。
b
$\frac{1}{\omega C}>\omega L$のとき回路は容量性を示す。
c
共振時の角周波数ωは$\frac{1}{\sqrt{LC}}$で表される。
d
共振時にはI=0である。
e
共振時にはVL=0かつVC=0である。
組み合わせ:
1. a b c
2. a b e
3. a d e
4. b c d
5. c d e
53
臨床工学技士国家試験 -
第24回 午後
正答率:51%
類似度 61.6%
図の回路の入力インピーダンスはどれか。ただし、Aは理想演算増幅器、jは虚数単位、ωは角周波数とする。(医用電気電子工学)
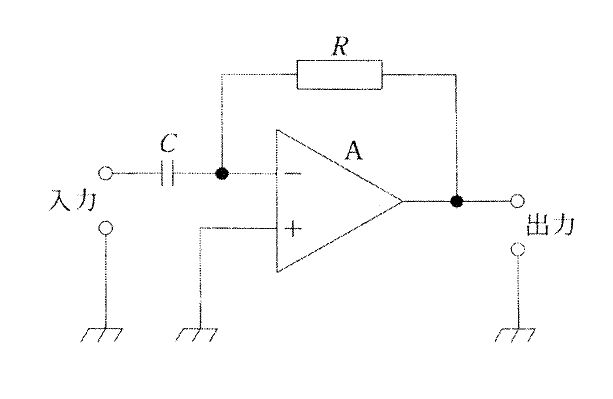
1
$ j\omega C$
2
$ \frac {1}{j\omega C}$
3
$ j\omega CR$
4
$ \frac {1}{j\omega CR}$
5
$ R+\frac {1}{j\omega C}$
50
臨床工学技士国家試験 -
第36回 午前
正答率:50%
類似度 61.2%
図の回路が共振状態にあるとき正しいのはどれか。
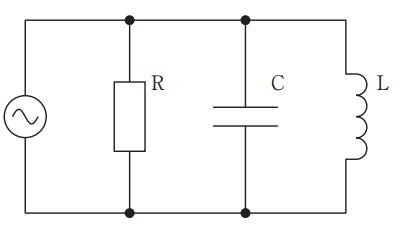
1
Rの抵抗値を2倍にすると、回路の全インピーダンスは4倍になる
2
Cの静電容量を2倍にすると、回路の全インピーダンスは1/2倍になる
3
Lのインダクタンスを2倍にすると、回路のアドミタンスは1/4倍になる
4
Cの静電容量を4倍にすると、共振周波数は1/2倍になる
5
Rの抵抗値を4倍にすると共振周波数は2倍になる
広告
51
臨床工学技士国家試験 -
第23回 午前
正答率:86%
類似度 60.1%
共振周波数がfであるRLC直列回路がある。Cを求める関係式はどれか。
1
$ \frac {1}{2\pi fL}$
2
$ \frac {1}{4\pi fL}$
3
$ \frac {L}{2\pi fL}$
4
$ \frac {L}{4\pi f^{2}}$
5
$ \frac {1}{4\pi ^{2}f^{2}L}$
広告