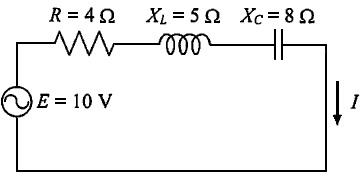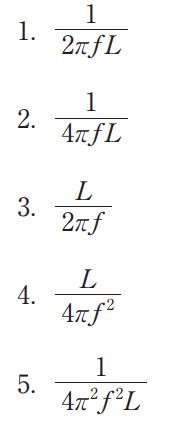第18回国試午後11問の類似問題
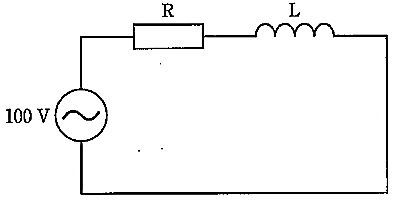
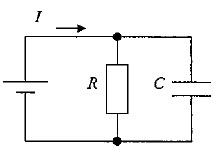
国試第21回午後:第8問
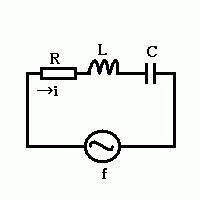
図の回路のインピーダンスの絶対値はどれか。ただし、ωは角周波数である。
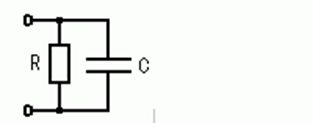
1: $ \sqrt {R+\frac {1}{\omega ^{2}c^{2}}}$
2: $ \sqrt {R^{2}+\omega ^{2}c^{2}}$
3: $ \frac {1}{\sqrt {R^{2}+\omega ^{2}c^{2}}}$
4: $ \sqrt {\frac {1}{1+\omega ^{2}c^{2}\pi ^{2}}}$
5: $\frac {1}{\sqrt {1+\omega ^{2}c^{2}R^{2}}}$
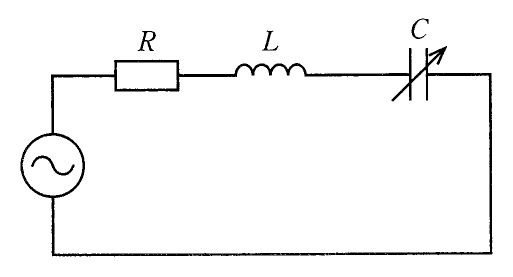
国試第22回午前:第50問
RLC直列回路に交流電圧を印加したときの印加電圧に対する電流の位相角θはどれか。ただし、ωは角周波数である。
1: $ \tan ^{-1}\left( \frac {L}{\omega CR}\right) $
2: $ \tan ^{-1}\left( \frac {R}{\omega CR}\right) $
3: $ \tan ^{-1}\left( \frac {R}{\frac {1}{\omega C}-\omega L}\right) $
4: $\tan ^{-1}\left( \frac {\frac {1}{\omega C}-\omega L}{R}\right)$
5: $ \tan ^{-1}\left( \frac {\omega L}{1+\omega CR}\right) $
国試第6回午後:第12問
コンデンサについて正しいのはどれか。
1: 蓄えられている電荷を2倍にすると電圧は1/2になる。
2: 2F(ファラッド)のコンデンサの両極板にそれぞれ±2Cの電荷が蓄えられているとき、電圧は1Vである。
3: 2Fのコンデンサの電圧が2Vであるとき、両極板に蓄えられている電荷は±2Cである。
4: 正弦波交流電圧を印加しているとき、電圧を2倍にすると流れる電流は1/2になる。
5: 正弦波電流を流しているとき、周波数を2倍にすると電圧は2倍になる。