第40回ME2午前30問の類似問題
国試第15回午後:第2問
図の回路のClに25μJのエネルギーが蓄えられているとき、C2に蓄えられている電荷はどれか。
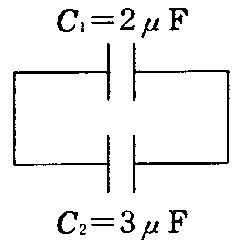
1: 3 μC
2: 5 μC
3: 12.5 μC
4: 15μC
5: 37.5 μC
- 答え:4
- 科目:医用電気電子工学 /電気工学 /電磁気学
- 重要度:集計中
- 類似問題を見る
- この問題について報告する
図の回路のClに25μJのエネルギーが蓄えられているとき、C2に蓄えられている電荷はどれか。

1: 3 μC
2: 5 μC
3: 12.5 μC
4: 15μC
5: 37.5 μC