臨床工学技士問題表示
臨床工学技士国家試験
解説
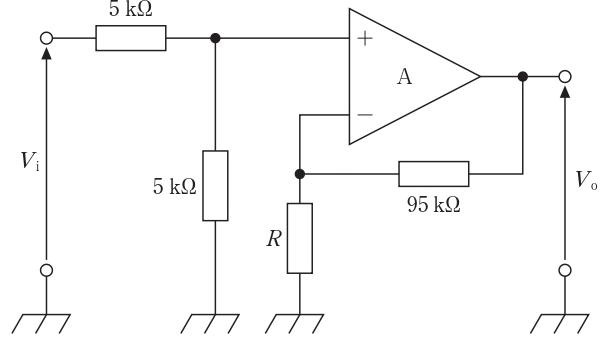
電圧利得が 20 dB のとき、線形利得は $A_v=10^{20/20}=10$。図は、入力 $V_i$ を 5 kΩと5 kΩの分圧で $V_+=V_i/2$ にし(理想OPで入力電流は流れず分圧は無負荷)、その電圧を非反転増幅回路で増幅する構成である。非反転増幅の利得は $A_{amp}=1+R_f/R_g=1+95\,[\mathrm{k\Omega}]/R$。全体利得は $A_{total}=(V_o/V_i)=(1/2)\times(1+95/R)$。これが 10 になるので、$10=(1/2)(1+95/R)\Rightarrow 1+95/R=20\Rightarrow R=95/19=5\,[\mathrm{k\Omega}]$。したがって R は 5 kΩ。
選択肢別解説
R=1 kΩ とすると $A_{amp}=1+95/1=96$、全体利得は $(1/2)\times 96=48$、$20\log_{10}48\approx33.6\,\mathrm{dB}$ で 20 dB にならないため不適。
R=2 kΩ とすると $A_{amp}=1+95/2=48.5$、全体利得は $(1/2)\times 48.5=24.25$、$20\log_{10}24.25\approx27.7\,\mathrm{dB}$。20 dB ではないため不適。
R=5 kΩ とすると $A_{amp}=1+95/5=20$、全体利得は $(1/2)\times 20=10$、$20\log_{10}10=20\,\mathrm{dB}$ を満たす。よって正答。
R=7 kΩ とすると $A_{amp}=1+95/7\approx14.57$、全体利得は $(1/2)\times14.57\approx7.29$、$20\log_{10}7.29\approx17.3\,\mathrm{dB}$。20 dB に届かないため不適。
R=10 kΩ とすると $A_{amp}=1+95/10=10.5$、全体利得は $(1/2)\times10.5=5.25$、$20\log_{10}5.25\approx14.4\,\mathrm{dB}$。20 dB ではないため不適。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
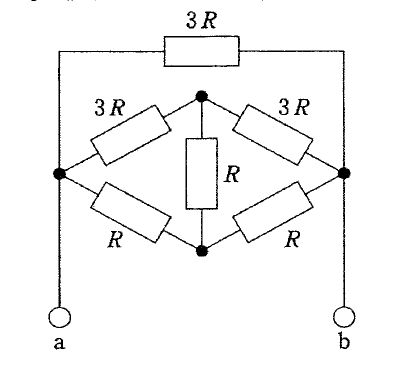
図の回路は、左右の節点(a・b)間に、(1) 上側の 3R、(2) 左上3R+右上3R の経路(直列で 6R)、(3) 左下R+右下R の経路(直列で 2R)、の3経路が並列に存在する形になる。これは中央の縦抵抗 R を含むブリッジが平衡(3R:3R = R:R)で、中央Rには電流が流れず取り除けるためである。したがって合成抵抗は、3R・6R・2Rの並列合成となり、$R_{ab}=\left(\tfrac{1}{3R}+\tfrac{1}{6R}+\tfrac{1}{2R}\right)^{-1}=\left(\tfrac{2+1+3}{6R}\right)^{-1}=\tfrac{6R}{6}=R$。よって正答は R。
選択肢別解説
誤り。上側の経路(3R)だけや上枝の直列(6R)のみを見た誤り。実際は 3R・6R・2R の並列で、合成は $R_{ab}=R$ と 6R より小さくなる。
誤り。3R は一枝の値であり並列合成ではこれより小さくなる。計算により $R_{ab}=R$。
誤り。並列合成は最小枝(2R)より必ず小さくなる。実際に計算すると $R_{ab}=R$。
正しい。ブリッジが平衡(3R:3R = R:R)なので中央Rを除去でき、残りは 3R・6R・2R の並列。$R_{ab}=\left(\tfrac{1}{3R}+\tfrac{1}{6R}+\tfrac{1}{2R}\right)^{-1}=R$。
誤り。並列合成の結果は $R$ であり $R/2$ にはならない。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
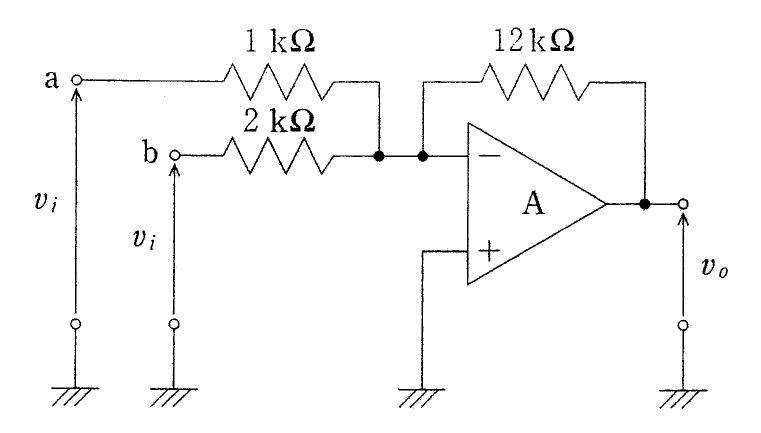
$本回路は非反転端子が接地された理想オペアンプの反転加算回路である。したがって反転入力端子は仮想接地となり電位は 0 V とみなせる。入力 a, b からの電流はそれぞれ I1 = (v_i - 0)/R1 = v_i/1 kΩ、I2 = (v_i - 0)/R2 = v_i/2 kΩ。これらが合流して帰還抵抗 Rf(=12 kΩ) に流れるので、KCLより I_f = I1 + I2 = v_i(1/1 kΩ + 1/2 kΩ) = 1.5 v_i/kΩ。出力電圧は反転端子側の電流と極性より v_o = - R_f I_f = -12 kΩ \times 1.5 v_i/kΩ = -18 v_i。$
選択肢別解説
反転加算器の一般式は $v_o = -\left(\frac{R_f}{R_1} + \frac{R_f}{R_2}\right) v_i$。$R_f=12\,\text{k}\Omega, R_1=1\,\text{k}\Omega, R_2=2\,\text{k}\Omega$ を代入すると $v_o=-18v_i$ であり、$-2v_i$ は不適。
同様に計算すると $v_o=-18v_i$。$-4v_i$ は抵抗比を誤った結果で誤り。
計算結果は $v_o=-18v_i$。$-6v_i$ は合成利得 $\frac{R_f}{R_1}+\frac{R_f}{R_2}$ を $6$ と取り違えた誤答。
$v_o=-18v_i$ が正しい。$-12v_i$ は $R_2\to\infty$(b入力なし)に相当する場合の値であり、本条件では不正解。
理想オペアンプの仮想接地と KCL より $I_1=v_i/1\,\text{k}\Omega, I_2=v_i/2\,\text{k}\Omega$、合流電流は $1.5\,v_i/\text{k}\Omega$。よって $v_o=-12\,\text{k}\Omega\times 1.5\,v_i/\text{k}\Omega=-18v_i$ となり正しい。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
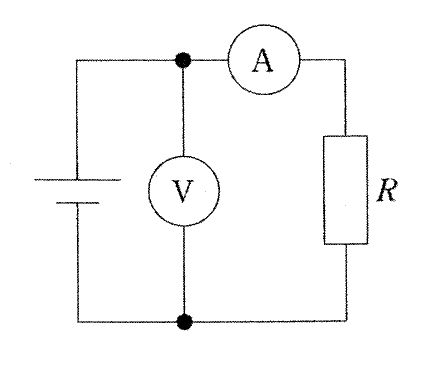
図より、電流計A(内部抵抗 r=2.0\Omega)と抵抗 R は直列、電圧計Vはその両端に並列で接続されている。電圧計の指示 1.0 V は直列合成抵抗 $(R+r)$ にかかる電圧、電流計の指示 20 mA はその回路電流である。よってオームの法則より $V=I(R+r)$。I=20 mA=0.020 A を用いて $1.0=0.020(R+2.0)$ から $R+2.0=50$ 、したがって $R=48\Omega$ となる。
選択肢別解説
誤り。R=45\Omega とすると合成は R+r=47\Omega、電流は $I=V/(R+r)=1/47\approx21.3\,\mathrm{mA}$ となり、指示 20 mA と一致しない。
正しい。電圧計の 1.0 V は直列合成抵抗 $(R+r)$ にかかる電圧で、$V=I(R+r)$。$1.0=0.020(R+2.0)$ より $R+2.0=50$、$R=48\Omega$。
誤り。内部抵抗 r=2.0\Omega を無視して $R=V/I=1.0/0.020=50\Omega$ とした誤り。実際は R に r が直列に加わるため、R は 50 から r を差し引く必要がある。
誤り。R=52\Omega では合成が 54\Omega となり、$I=1/54\approx18.5\,\mathrm{mA}$ と 20 mA に一致しない。また、総抵抗 50\Omega に r=2\Omega を加える誤った処理に対応する。
誤り。R=55\Omega では合成が 57\Omega、$I=1/57\approx17.5\,\mathrm{mA}$ と指示値と一致しない。与条件 r=2.0\Omega を用いた $V=I(R+r)$ を満たさない。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
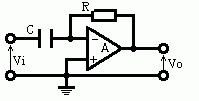
画像の回路は、入力側がコンデンサC、帰還が抵抗R、非反転端子(+)が接地の反転構成である。理想オペアンプでは仮想接地より反転端子電位は約0 Vなので、入力コンデンサ電流は $i_C=C\frac{\mathrm{d}}{\mathrm{d}t}(V_i-0)=C\frac{\mathrm{d}V_i}{\mathrm{d}t}$。この電流がそのまま帰還抵抗を流れ、抵抗電流は $i_R=(0-V_o)/R=-V_o/R$。節点で $i_C=i_R$ より、$C\frac{\mathrm{d}V_i}{\mathrm{d}t}=-\frac{V_o}{R}$、従って入出力関係は $V_o=-CR\,\frac{\mathrm{d}V_i}{\mathrm{d}t}$。符号が負になるのは反転動作による。したがって正解は選択肢2である。
選択肢別解説
誤り。形は微分回路だが係数が逆である。導出より $V_o=-CR\,\frac{\mathrm{d}V_i}{\mathrm{d}t}$ が正しく、$-\frac{1}{CR}$ ではない。
正しい。入力にC、帰還にRをもつ反転構成の理想微分回路であり、仮想接地と電流連続から $V_o=-CR\,\frac{\mathrm{d}V_i}{\mathrm{d}t}$ となる。
誤り。これは積分回路(入力に抵抗、帰還にコンデンサ)の関係式 $V_o=-\frac{1}{CR}\int V_i\,\mathrm{d}t$ であり、本回路(入力C・帰還Rの微分回路)には当てはまらない。
誤り。形が積分回路で係数も不適切。本回路は微分回路であり、正しい関係は $V_o=-CR\,\frac{\mathrm{d}V_i}{\mathrm{d}t}$。
誤り。積分形かつ係数が不正(次元的にも不整合)。理想積分回路の係数は $-\frac{1}{CR}$ であり、本回路は微分回路である。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
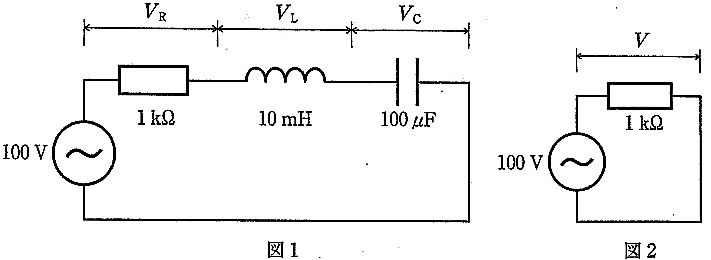
直列RLC回路のインピーダンスは $Z=R+j(\omega L-1/(\omega C))$。共振時は $\omega L=1/(\omega C)$ となり虚数成分が0、したがって合成インピーダンスは実数の $R$ のみ。よって図1では電源電圧と抵抗電圧が一致し $V_R=V_\text{src}=100\,\mathrm{V}$。図2は抵抗のみの直列回路で、理想電源に対して抵抗両端電圧 $V$ も電源電圧と等しく $V=100\,\mathrm{V}$。ゆえに比は $V_R/V=100/100=1$。なお共振角周波数は $\omega_0=1/\sqrt{LC}$(数値は比の計算には不要)。
選択肢別解説
$1/2$ となる条件は本設問には当てはまらない。共振時の直列RLCでは合成インピーダンスは $R$ のみで、抵抗電圧は電源電圧と等しいため、比は1である。
$1/\sqrt{2}$ は電力や実効値の文脈で現れやすいが、ここでは共振時に $V_R=V_\text{src}$、図2でも $V=V_\text{src}$ であるため、比は1となる。
正しい。共振で $\omega L=1/(\omega C)$ となり $Z=R$。したがって図1で $V_R=V_\text{src}$。図2は抵抗のみで $V=V_\text{src}$。よって $V_R/V=1$。
$\sqrt{2}$ となる根拠はない。共振直列回路ではリアクタンスが打ち消し合い、抵抗電圧は電源電圧と等しくなるので比は1。
2倍にはならない。共振でもコイルやコンデンサ単体の電圧が大きくなることはあるが、抵抗電圧は電源電圧と等しく、比は1である。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
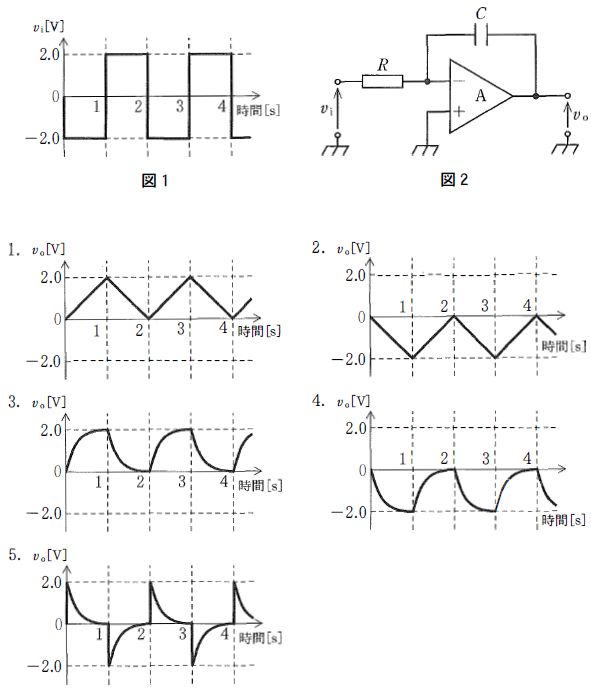
ただし、A は理想演算増幅器とし、$v_o$ の初期値は 0V、$CR=1s$ とする。
解説
図2は反転形(ミラー)積分回路で、理想OPアンプかつ初期値 $v_o(0)=0$、$CR=1\,\mathrm{s}$ より入出力関係は $v_o(t)=-\frac{1}{CR}\int v_i(t)\,dt=-\int v_i(t)\,dt$、すなわち傾きは $\frac{dv_o}{dt}=-v_i$ となる。図1の入力は0–1 sで $v_i=+2\,\mathrm{V}$、1–2 sで $v_i=-2\,\mathrm{V}$ が交互に続く矩形波である。したがって0–1 sは傾き −2 V/s で $0\,\mathrm{V}\to -2\,\mathrm{V}$、1–2 sは傾き +2 V/s で $-2\,\mathrm{V}\to 0\,\mathrm{V}$ と直線的に変化する。この動作が繰り返されるため、出力は0 Vと −2 Vの間を往復する三角波となる。画像の選択肢図からは、この波形に一致するのは選択肢2である。
選択肢別解説
誤り。選択肢1の波形は0→+2 V→0→+2 V…と正側に三角状に振れる。反転積分器では $\frac{dv_o}{dt}=-v_i$ のため、$v_i=+2\,\mathrm{V}$ の区間では出力は負方向(−2 V/s)へ直線的に下がり、初期値0 Vから −2 Vに到達するはずで正側へは上がらない。
正しい。0–1 sで $v_i=+2\,\mathrm{V}$ より傾き −2 V/s、$0\to -2\,\mathrm{V}$。1–2 sで $v_i=-2\,\mathrm{V}$ より傾き +2 V/s、$-2\to 0\,\mathrm{V}$。これが周期的に繰り返されるため、0 Vと −2 V間の三角波となる。
誤り。選択肢3は指数関数的に丸みを帯びた充放電状の波形で、受動RC回路の応答に近い。理想OPアンプの積分器では区間ごとに傾き一定の直線(三角波)となるため一致しない。
誤り。選択肢4も指数的な曲線で、直線的な傾きが得られる理想積分器の出力と合致しない。また0–1 sで負側へ直線的に −2 Vまで降下する特徴を満たしていない。
誤り。選択肢5は各立ち上がり付近で鋭い過渡を示す波形で、微分的応答に近い。積分器の出力は矩形入力に対し時間に対して線形に変化する三角波となる。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
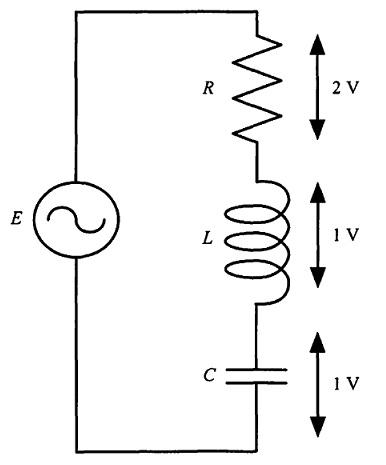
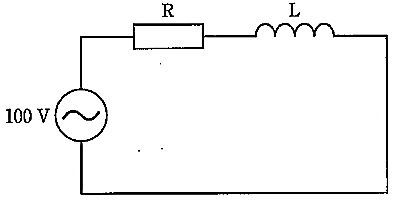
正弦波のRL直列回路では、抵抗Rの電圧は電流と同相、コイルLの電圧は電流より90°進むため、電源電圧Eはベクトル的に $E^2=V_R^2+V_L^2$ の関係になる(直角三角形)。図より電源は100 V、与えられた抵抗電圧は60 Vなので、コイル電圧は $V_L=\sqrt{E^2-V_R^2}=\sqrt{100^2-60^2}=\sqrt{6400}=80$ V。したがって答えは80 V。
選択肢別解説
0 Vであればコイルに電圧降下が生じないが、RL直列で電源100 V・抵抗電圧60 Vの条件では $E^2=V_R^2+V_L^2$ を満たす必要があり、$V_L=80$ Vとなる。よって不適。
RL直列回路の電圧は直交関係にあり $E^2=V_R^2+V_L^2$。$E=100$ V、$V_R=60$ Vから $V_L=80$ Vであり、20 Vは一致しない。
同上のベクトル和より $V_L=\sqrt{100^2-60^2}=80$ Vである。40 Vは条件と矛盾。
抵抗電圧と同じ60 Vとなるのは一般には成立しない。$E^2=V_R^2+V_L^2$ より $V_L=80$ Vであり、60 Vは不正解。
RL直列で $E^2=V_R^2+V_L^2$。$E=100$ V、$V_R=60$ Vより $V_L=\sqrt{100^2-60^2}=80$ V。これが正解。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。