臨床工学技士問題表示
臨床工学技士国家試験
解説
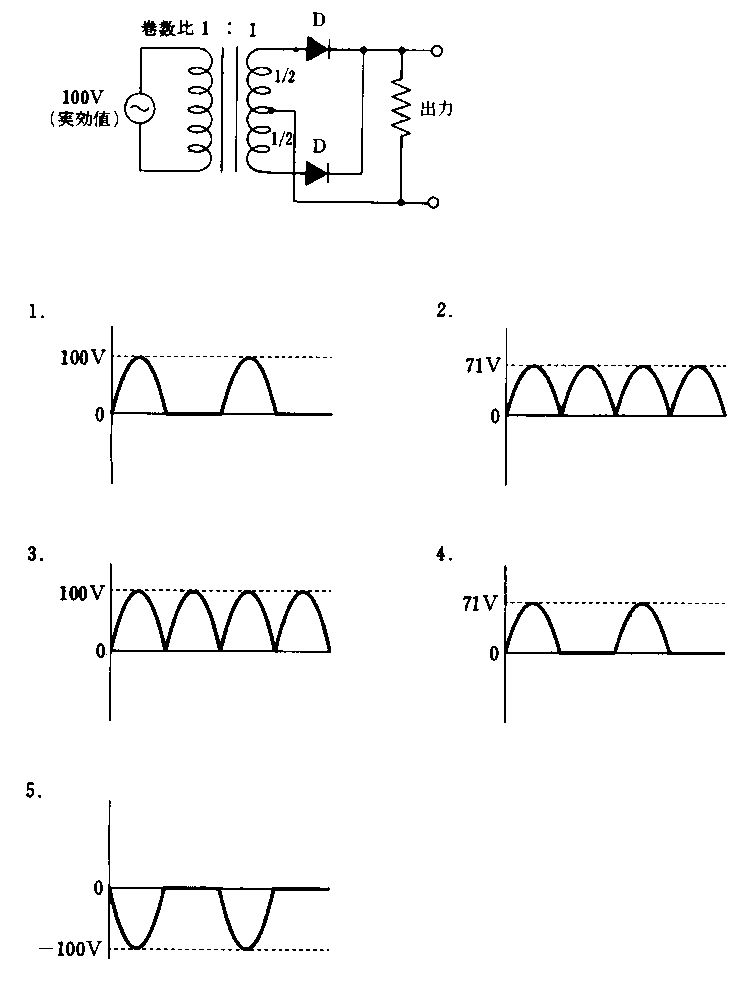
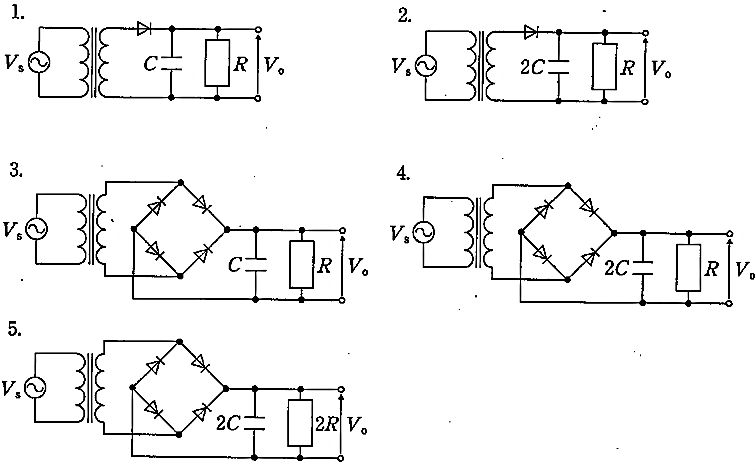
リプル率を小さくする要点は、(1) 整流後のリプル周波数を高くする(全波整流は半波の2倍の周波数)、(2) CR平滑の時定数 $\tau=RC$ を大きくすること。画像の5つの回路は、1・2が半波、3・4・5が全波で、各回路の時定数は1:$CR$, 2:$2CR$, 3:$CR$, 4:$2CR$, 5:$4CR$(2Cと2Rの組合せ)となる。リプルの大きさは概ね $\propto 1/(f_r RC)$($f_r$ はリプル周波数)なので、全波で $f_r=2f$ かつ $RC$ が最大の回路5が最もリプル率が小さい。
選択肢別解説
半波整流でリプル周波数は $f_r=f$、時定数は $CR$。全波やより大きな時定数の回路に比べてリプルが大きく、最小にはならない。
半波整流($f_r=f$)で時定数は $2CR$。回路1よりはリプルが減るが、全波整流($f_r=2f$)かつ時定数の大きい回路には及ばないため最小ではない。
全波整流($f_r=2f$)で時定数は $CR$。半波より有利だが、時定数が小さく回路4や5に比べてリプルは大きい。
全波整流($f_r=2f$)で時定数は $2CR$。回路3よりリプルは小さいが、回路5の $4CR$ には及ばず最小ではない。
全波整流($f_r=2f$)で、コンデンサ2Cと負荷2Rから時定数は $4CR$(最大)。リプルは概ね $\propto 1/(f_r RC)$ に従い最小となる。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
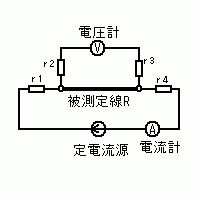
四端子法では、被測定抵抗Rの両端電圧を電圧計で直接測るため、電流端子側のリード・接触抵抗r1, r4による電圧降下は測定に現れず、電圧端子側のr2, r3にも電圧計電流がほぼ流れないので影響は無視できる。電圧計の内部抵抗は1 MΩで、電圧計に流れる電流は約 V/Rv = 0.05 V / 1,000,000 Ω = 5×10^{-8} A と極めて小さい。したがってRはオームの法則で $R=\frac{V}{I}=\frac{0.05}{0.25}=0.2\,\Omega$ と求まる。
選択肢別解説
誤り。四端子法ではRのみの電圧降下を測定し、$R=V/I=0.05/0.25=0.2\,\Omega$。0.1\,ΩとなるのはVが0.025\,Vの場合で、本条件に合わない。
正しい。四端子法でリード・接触抵抗の影響を排除でき、$R=\frac{0.05}{0.25}=0.2\,\Omega$。電圧計の内部抵抗1\,MΩにより電圧計回路電流は50\,nA程度で無視できる。
誤り。$R=V/I$より0.3\,ΩにするにはV=0.075\,Vが必要。四端子法ではr1〜r4の影響は測定電圧に現れないため、0.3\,Ωにはならない。
誤り。0.4\,ΩにするにはV=0.10\,Vが必要だが、実測は0.05\,V。四端子法によりリード・接触抵抗の加算はない。
誤り。0.5\,ΩにするにはV=0.125\,Vが必要。実測値および四端子法の特性から該当しない。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
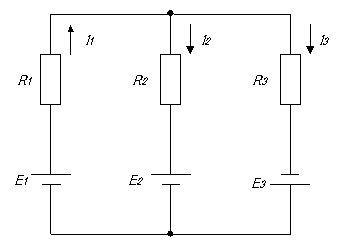
図の上下2ノードに3枝(R1–E1,R2–E2,R3–E3)が接続された並列回路で、電流の向きは画像で I1 が上向き、I2・I3 が下向き。上側ノードにキルヒホッフ第1法則(KCL)を適用すると、流入 I1 と流出 I2・I3 の関係から $I1 - I2 - I3 = 0$ が成り立つ。電圧については、各枝の上端と下端は同電位差で結ばれているため、任意の2枝で閉回路を作ってキルヒホッフ第2法則(KVL)を適用すると、左枝と中央枝のループで $I1\,R1 + I2\,R2 = E1 - E2$、中央枝と右枝のループで $-I2\,R2 + I3\,R3 = E2 + E3$ が得られる。外側ループ(左枝と右枝)では $I1\,R1 + I3\,R3 = E1 + E3$ となるため、$E1 - E3$ とする式は符号が不一致となり誤りである。
選択肢別解説
正しい。上側ノードにKCLを適用。画像では I1 はノードへ流入、I2・I3 はノードから流出なので、流入=流出より $I1 = I2 + I3$、すなわち $I1 - I2 - I3 = 0$。
誤り。$E1/R1$ は左枝単独のオームの法則による電流 $I1$ を表す量で、全枝電流の和 $I1+I2+I3$ と一般には一致しない。KCL・KVLのいずれからも導けない。
誤り。左枝と右枝でつくる外側ループにKVLを適用すると、起電力は加算され $E1 + E3$、電圧降下は $I1 R1 + I3 R3$ となる。よって正しくは $I1 R1 + I3 R3 = E1 + E3$ であり、$E1 - E3$ とするこの式は符号が不正。
正しい。左枝と中央枝のループにKVLを適用。抵抗での電圧降下の総和 $I1 R1 + I2 R2$ は、図の極性に従った起電力の差 $E1 - E2$ に等しい。
正しい。中央枝と右枝のループにKVLを適用。巡回方向と I2 の向きが逆になるため中央枝の抵抗降下は $-I2 R2$、右枝は $+I3 R3$。起電力は加算され $E2 + E3$ なので、$-I2 R2 + I3 R3 = E2 + E3$ が成り立つ。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
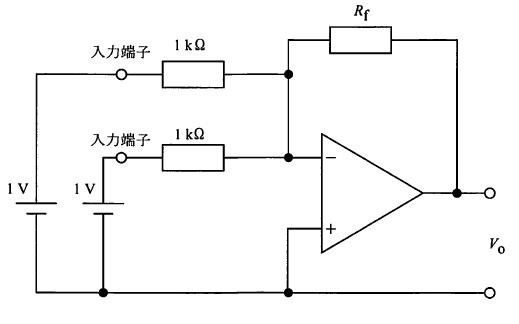
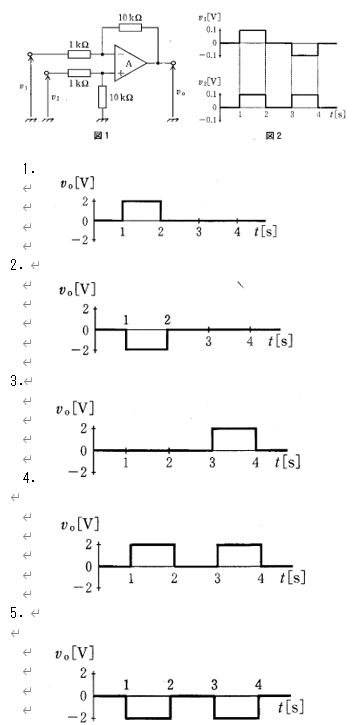
図1は理想演算増幅器Aを用いた差動増幅回路で、図から両入力の直列抵抗が1 kΩ、帰還側と非反転側の抵抗が10 kΩで対になっているため、差動利得は $\frac{R_f}{R_1}=10$ となる。よって出力は $v_o=10\,(v_2-v_1)$。図2の入力波形より、v1は1〜2 sで+0.1 V、3〜4 sで−0.1 V、その他0 V。v2は2〜3 sで−0.1 V、3〜4 sで+0.1 V、その他0 V。これを代入すると、0〜1 s:0 V、1〜2 s:10(0−0.1)=−1 V、2〜3 s:10((−0.1)−(−0.1))=0 V、3〜4 s:10(0.1−(−0.1))=+2 V、4〜5 s:0 V。従って、この出力波形に一致するのは選択肢3である。
選択肢別解説
図中の選択肢1は1〜2 sで+1 V、3〜4 sで0 Vを示すが、計算上は1〜2 sで−1 V、3〜4 sで+2 Vとなるため、符号・振幅ともに一致しない。
図中の選択肢2は1〜2 sで−1 Vまでは一致するが、3〜4 sが0 Vとなっており、本来の+2 Vと合わないため不正解。
図中の選択肢3は0〜1 s:0 V、1〜2 s:−1 V、2〜3 s:0 V、3〜4 s:+2 V、4〜5 s:0 Vを示し、式 $v_o=10\,(v_2-v_1)$ と図2の入力値から得られる結果と完全に一致するため正しい。
図中の選択肢4は1〜2 sで+1 Vとなっており、計算結果の−1 Vと符号が異なる。3〜4 sの+2 Vは一致するが、全区間では一致しないため不正解。
図中の選択肢5は1〜2 sで−1 Vは一致するが、3〜4 sで−2 Vとなっており、計算上は+2 Vであるため符号が逆で不正解。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
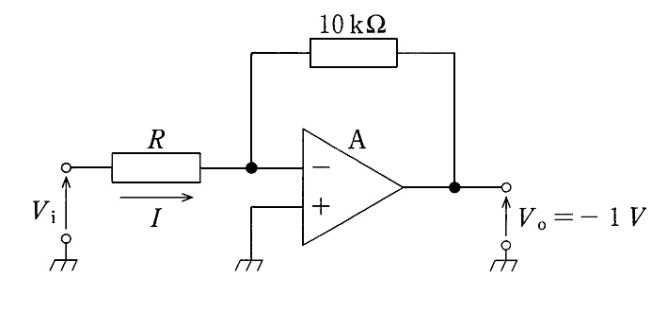
解説
理想オペアンプの反転増幅回路で、帰還抵抗は 10 kΩ、入力抵抗は R。電圧増幅度が 20 dB なので、$20\log_{10}\lvert A_v\rvert=20\Rightarrow\lvert A_v\rvert=10$、かつ $A_v=-R_f/R$ より $R=R_f/10=1\,\mathrm{k}\Omega$。図より出力は $V_o=-1\,\mathrm{V}$ で、理想条件下では反転入力は仮想接地で 0 V。したがって $V_i=V_o/A_v=(-1)/(-10)=0.1\,\mathrm{V}$、抵抗 R を流れる電流は $I=V_i/R=0.1\,\mathrm{V}/1\,\mathrm{k}\Omega=1.0\times10^{-4}\,\mathrm{A}=0.1\,\mathrm{mA}$。同じ結果は、帰還抵抗 10 kΩ に 1 V が印加されている(0 V と −1 V の差)ことから $I=1\,\mathrm{V}/10\,\mathrm{k}\Omega=0.1\,\mathrm{mA}$ としても得られる。
選択肢別解説
0.01 mA は 10 倍小さい。$\lvert A_v\rvert=10$、$R=1\,\mathrm{k}\Omega$、$V_i=0.1\,\mathrm{V}$ より $I=V_i/R=0.1/1000=0.0001\,\mathrm{A}=0.1\,\mathrm{mA}$ となる。
正しい。$20\,\mathrm{dB}\Rightarrow\lvert A_v\rvert=10$、$A_v=-R_f/R$、$R_f=10\,\mathrm{k}\Omega$ から $R=1\,\mathrm{k}\Omega$。$V_o=-1\,\mathrm{V}$ より $V_i=0.1\,\mathrm{V}$、$I=0.1\,\mathrm{V}/1\,\mathrm{k}\Omega=0.1\,\mathrm{mA}$。仮想接地を用いれば $I=1\,\mathrm{V}/10\,\mathrm{k}\Omega=0.1\,\mathrm{mA}$ とも求まる。
1 mA は 10 倍大きい。10 kΩ に 1 V がかかっているため、オームの法則で流れる電流は最大でも $1/10\,000=0.0001\,\mathrm{A}=0.1\,\mathrm{mA}$。
10 mA は 100 倍以上大きく不適切。10 kΩ に 1 V なら $I=0.1\,\mathrm{mA}$ であり、10 mA にはならない。
100 mA は桁違い。10 kΩ に 1 V で $I=0.1\,\mathrm{mA}$ であるため、100 mA は物理的にありえない。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
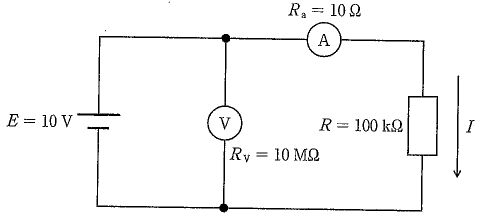
解説
回路は、上枝に電流計の内部抵抗 R_a=10\,\Omega と抵抗 R=100\,\text{k}\Omega が直列、下枝に電圧計の内部抵抗 R_V=10\,\text{M}\Omega が接続された並列回路で、電源は理想(内部抵抗無視)で E=10\,V である。理想電源なので各枝の端子電圧は常に 10 V に固定され、下枝(電圧計)にどれだけ電流が流れても上枝の電流値には影響しない。したがって R を流れる電流 I は上枝の直列合成抵抗 R+R_a に対してオームの法則より $ I=\frac{E}{R+R_a}=\frac{10}{100\,000+10}\,\text{A}\approx9.999\times10^{-5}\,\text{A}=0.09999\,\text{mA}\approx0.1\,\text{mA} $。R に比べて R_a は極めて小さいため、近似的に $I\approx E/R$ としても同じ選択肢に到達する。
選択肢別解説
正しい。理想電源で上枝の電流は $ I=\frac{E}{R+R_a}=\frac{10\,\text{V}}{100\,000\,\Omega+10\,\Omega}\approx0.09999\,\text{mA}\approx0.1\,\text{mA} $。
$誤り。計算値は約 0.1 mA であり、0.2 mA となるには合成抵抗がおよそ 50 k\Omega 程度でなければならないが、本回路では R+R_a\approx100 k\Omega である。$
$誤り。1 mA となるのは合成抵抗が約 10 k\Omega の場合であり、本回路の R+R_a は約 100 k\Omega と 10 倍大きい。$
$誤り。2 mA となるには合成抵抗が約 5 k\Omega 必要だが、実際は約 100 k\Omega である。$
$誤り。10 mA は合成抵抗が約 1 k\Omega のときの値で、本回路の抵抗値とは一致しない。$
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
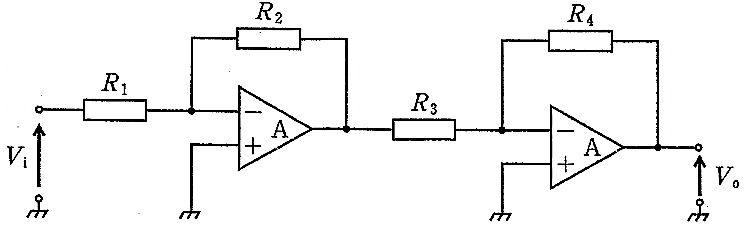
解説
画像の回路は、非反転端子が接地された反転増幅回路を2段直列に接続した構成である。理想OPアンプかつ負帰還成立より各段の反転端子は仮想接地となる。第1段は入力抵抗がR1、帰還抵抗がR2の反転増幅器で、利得は $A_1=-\frac{R_2}{R_1}$。第2段は入力抵抗がR3、帰還抵抗がR4の反転増幅器で、利得は $A_2=-\frac{R_4}{R_3}$。直列接続の全体利得は積となるため、$\frac{V_o}{V_i}=A_1A_2=\left(-\frac{R_2}{R_1}\right)\left(-\frac{R_4}{R_3}\right)=\frac{R_2R_4}{R_1R_3}$。反転が2回行われるため全体の位相は元に戻り、正符号になる。
選択肢別解説
正しい。2段の反転増幅回路の利得は $\left(-\frac{R_2}{R_1}\right)\times\left(-\frac{R_4}{R_3}\right)=\frac{R_2R_4}{R_1R_3}$ となり正符号である。
誤り。2段の反転で位相は再び非反転(正相)になるため、全体利得は正でなければならない。大きさ自体は一致するが符号が誤り。
誤り。分子・分母が逆である。正しい全体利得は $\frac{R_2R_4}{R_1R_3}$。
誤り。分子・分母が逆であるうえ、符号も負で不適切。2段反転のため正符号になる。
誤り。式は $\frac{R_1R_3}{R_1R_4}=\frac{R_3}{R_4}$ に簡約され、R2が含まれず回路の物理対応(第1段: R2/R1、第2段: R4/R3)を反映していない。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
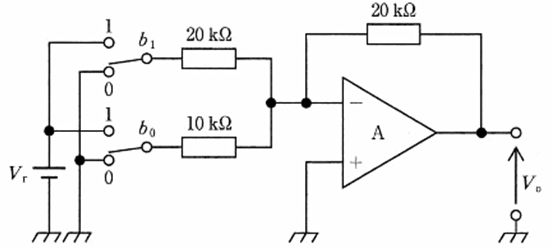
解説
本回路は反転加算回路であり、理想演算増幅器の仮想短絡により反転入力端子は 0 V(仮想接地)となる。b0=1、b1=1 のとき Vr が 20 k\Omega と 10 k\Omega の両入力抵抗に同時に印加されるため、流入電流はそれぞれ $V_r/20\,\text{k}\Omega$ と $V_r/10\,\text{k}\Omega$ の合計となる。入力端子には電流が流れないため、この合流電流がそのまま帰還抵抗 20 k\Omega を流れ、$V_o=-R_f\,(V_r/20\,\text{k}\Omega+V_r/10\,\text{k}\Omega)=-20\,(1/20+1/10)V_r=-(1+2)V_r=-3V_r$ となる。したがって正答は -3V_r。別の見方として、各枝の利得は $-R_f/R_{in}$ なので 20 k\Omega 枝で -1、10 k\Omega 枝で -2、和で -3。
選択肢別解説
誤り。b0=1、b1=1 では両入力から電流が流れ、$V_o=-3V_r$ となる。$V_r=0$ の特殊な場合を除き 0 V にはならない。
誤り。-Vr は 20 k\Omega の枝のみが有効なときの寄与($-R_f/R_{in}=-20/20=-1$)に相当する。実際は 10 k\Omega 枝(-2倍)も加わるため合計は -3Vr。
誤り。-2Vr は 10 k\Omega の枝のみが有効($-20/10=-2$)な場合の出力であり、本問の b0=1、b1=1 ではさらに -1Vr が加わって -3Vr となる。
正しい。帰還抵抗 $R_f=20\,\text{k}\Omega$、入力抵抗が 20 k\Omega と 10 k\Omega で、$V_o=-(R_f/20\,\text{k}\Omega+R_f/10\,\text{k}\Omega)V_r=-(1+2)V_r=-3V_r$。
誤り。両入力の寄与の和は -1Vr と -2Vr の合計で -3Vr であり、-4Vr にはならない。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
内部抵抗 r をもつ起電力 E の電池に負荷 R を接続したとき、負荷での消費電力は $P(R)=I^2R=\left(\frac{E}{r+R}\right)^2 R$ で表される。$\frac{dP}{dR}=0$ から最大は整合負荷の条件 $R=r$ で生じる。よって $E=50\,\text{V},\ r=5\,\Omega$ では $R=5\,\Omega$ のとき最大となり、$P_{\text{max}}=\left(\frac{50}{5+5}\right)^2\times 5=125\,\text{W}$。一般式でも $P_{\text{max}}=\frac{E^2}{4r}=\frac{50^2}{4\times 5}=125\,\text{W}$ で一致する。
選択肢別解説
誤り。整合負荷 $R=r=5\,\Omega$ のときの最大電力は $P_{\text{max}}=125\,\text{W}$ であり、25 W にはならない。
誤り。負荷で取り出せる最大電力は整合負荷で $P_{\text{max}}=\frac{E^2}{4r}=125\,\text{W}$。50 W ではない。
正しい。$R=r=5\,\Omega$ で $P_{\text{max}}=\left(\frac{50}{5+5}\right)^2\times 5=125\,\text{W}$。また $\frac{E^2}{4r}=\frac{2500}{20}=125\,\text{W}$ とも計算できる。
誤り。$P_{\text{max}}=\frac{E^2}{4r}=125\,\text{W}$ が理論上の上限であり、250 W は取り得ない。
誤り。$P_{\text{max}}=125\,\text{W}$ を大きく上回る 500 W は取り得ない。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
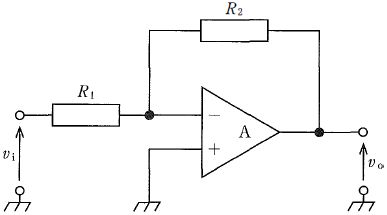
解説
図は理想演算増幅器Aを用いた反転増幅回路であり、反転入力は負帰還により仮想接地となる。このため外部から見た入力抵抗は入力抵抗そのものに等しく、$R_1=100\,\mathrm{k}\Omega$でなければならない。電圧増幅度は$dB$表記で与えられ、$G_{\mathrm{dB}}=20\log_{10}|A_v|$より$26=20\log_{10}|A_v|\Rightarrow |A_v|=10^{26/20}=10^{1.3}=10\times10^{0.3}\approx 10\times 2=20$(与えられた$\log_{10}2=0.3$を使用)。反転増幅回路では$|A_v|=R_2/R_1$であるから、$R_2=20\times 100\,\mathrm{k}\Omega=2\,\mathrm{M}\Omega$。よって$R_1=100\,\mathrm{k}\Omega,\ R_2=2\,\mathrm{M}\Omega$の組合せが適切である。
選択肢別解説
$R1=5 k\Omega では入力抵抗が5 k\Omegaとなり、与えられた100 k\Omegaの条件に反する。なおR2/R1=100/5=20で増幅率自体は満たすが、入力抵抗条件を満たさないため不適。$
R1=100 k\Omegaで入力抵抗条件は満たすが、R2/R1=1\,\mathrm{M\Omega}/100\,\mathrm{k\Omega}=10より$|A_v|=10$、$20\log_{10}10=20\,\mathrm{dB}$で26 dBに達しないため不適。
R1=100 k\Omegaで入力抵抗条件を満たし、R2/R1=2\,\mathrm{M\Omega}/100\,\mathrm{k\Omega}=20より$|A_v|=20$。$20\log_{10}20=20(\log_{10}10+\log_{10}2)=20(1+0.3)=26\,\mathrm{dB}$となり条件を満たすため適切。
$R1=200 k\Omegaでは入力抵抗が200 k\Omegaとなり条件の100 k\Omegaに反する。R2/R1=4\,\mathrm{M\Omega}/200\,\mathrm{k\Omega}=20で増幅度は満たすが、入力抵抗条件を満たさないため不適。$
R1=200 k\Omegaで入力抵抗条件に反するうえ、R2/R1=6\,\mathrm{M\Omega}/200\,\mathrm{k\Omega}=30より$20\log_{10}30\approx29.5\,\mathrm{dB}$で26 dBとも一致しないため不適。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
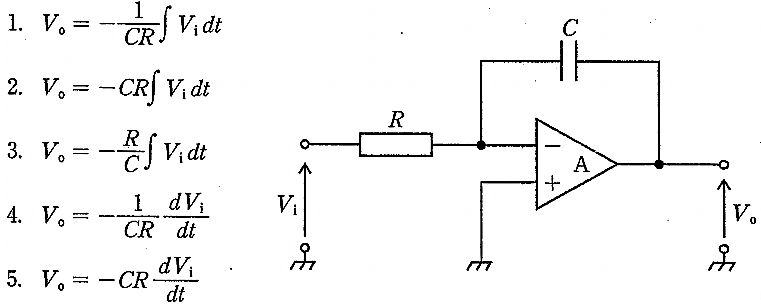
解説
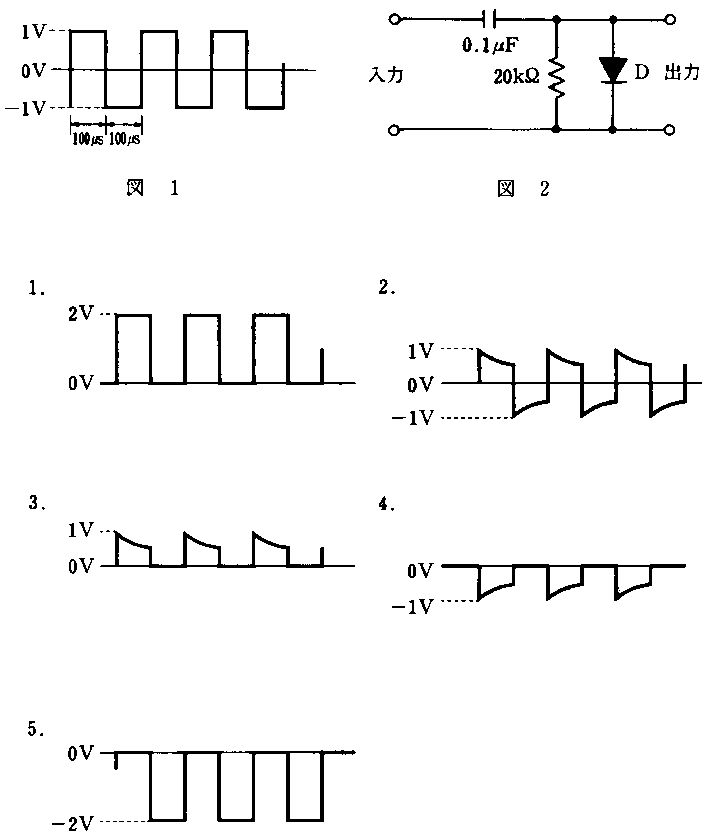
$図の回路は、非反転入力が接地され、入力Viが抵抗Rを介して反転入力へ、出力Voから反転入力へコンデンサCで帰還する理想OPアンプの反転積分回路である。理想OPアンプでは仮想短絡が成り立ち反転入力の電位は0 V。反転入力ノードでのKCLより、Rを流れる電流は i_R = \frac{V_i}{R}、コンデンサ電流は i_C = C\,\frac{d(0 - V_o)}{dt} = -C\,\frac{dV_o}{dt}。よって \frac{V_i}{R} = -C\,\frac{dV_o}{dt} ⇒ \frac{dV_o}{dt} = -\frac{1}{RC}V_i。両辺を時間積分して、初期条件(コンデンサ初期電荷 \cdot オフセットを無視)を0とすれば、求める入出力関係は V_o = -\frac{1}{CR}\int V_i\,dt となる。したがって正解は選択肢1。2 \cdot 3は係数が誤り、4 \cdot 5は微分回路の式である。$
選択肢別解説
$選択肢1は V_o = -\frac{1}{CR}\int V_i\,dt を示し、反転積分回路の正しい入出力関係である。仮想短絡とKCLから \frac{dV_o}{dt} = -\frac{1}{RC}V_i を得て時間積分するとこの式になる。負号は反転入力構成による極性反転に由来する。$
$V_o = -CR\int V_i\,dt を示すが、係数の次元が [CR] となり、RCの逆数であるべき積分回路の係数として不適。導出からも -\frac{1}{RC} が正しいため不正解。$
$V_o = -\frac{R}{C}\int V_i\,dt を示すが、係数が -\frac{1}{RC} ではなく -\frac{R}{C} となっており誤り。次元解析でも [R/C] は [1/RC] と一致しない。$
$V_o = -\frac{1}{CR}\frac{dV_i}{dt} は入力の微分に比例する式で、反転微分回路の特徴。今回の回路は帰還素子がC、入力側がRであり、入出力は積分関係になるため不適。$
$V_o = -CR\frac{dV_i}{dt} も微分回路の形式であり、本回路(積分回路)の入出力式ではない。係数および演算(微分)が不適。$
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。