臨床工学技士問題表示
臨床工学技士国家試験
解説
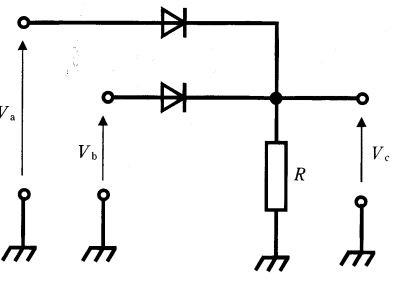
図の回路は2本の理想ダイオードで入力Va, Vbから1点に合流し、その点を抵抗Rで接地するダイオードOR回路である。理想ダイオードは順方向で電圧降下0V、逆方向は完全に遮断となるため、出力ノードVcは有効な入力のうち最大電圧に引き上げられる。Va=5V、Vb=3Vでは、Va側ダイオードが順方向に導通してノードを5Vまで引き上げ、同時にVb側ダイオードはアノード3V・カソード5Vで逆バイアスとなり遮断される。従ってVc=5Vとなる。
選択肢別解説
-2Vは誤り。回路に負電源は無く、ダイオードは左(入力)から右(出力)への向きで配置されているため、出力ノードが負電位になる機構がない。抵抗は接地へのプルダウンであり、負電位を発生させない。
2Vは誤り。理想ダイオードOR回路では出力は入力のうち高い方に一致する。本条件では5Vと3Vのうち高い5Vとなるため2Vにはならない。
3Vは誤り。Va=5Vが存在すると、Va側ダイオードが導通してノードを5Vに引き上げ、Vb側はアノード3V、カソード5Vで逆バイアスとなり遮断されるため、3Vは出力されない。
5Vが正解。理想ダイオードOR回路では出力は入力の最大値となる。Va=5V、Vb=3Vより、Va側だけが有効に導通してノードVcは5Vとなる。
8Vは誤り。2つの入力を加算する回路ではなく、ダイオードORは高い方の電圧のみを出力する。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
図2のように上限をE1、下限をE2で打ち切る出力は、直流基準E1・E2に対して一方通行に動作する2本の理想ダイオードを互いに逆向き(アンチパラレル)で用いた両側クリップ回路で得られる。入力ViがE1を超えると上側のダイオードが導通して出力VoはE1に張り付き、ViがE2を下回ると下側のダイオードが導通してVoはE2に張り付く。E2≦Vi≦E1の範囲では両ダイオードとも遮断され、Vo≈Viとなる。理想ダイオード前提のため順方向電圧降下は0 Vとみなされ、閾値はちょうどE1・E2となる。したがって、この条件を満たす回路が正答となる。
選択肢別解説
不正解。両側クリップを実現するには、各ダイオードが対応する基準電圧(E1またはE2)に対して適切な極性で接続され、ViがE1超過時・E2未満時にのみ導通する必要がある。本選択肢の詳細回路は本文中に欠落しており特定できないが、提示条件(両側をE1とE2で明確に打ち切る)を満たす接続にはならないため、所望のVo(図2)は得られない。
不正解。両側クリップには上限用・下限用の2本のダイオードを互いに逆向きに用い、各々がE1・E2でクランプする必要がある。回路詳細は選択肢本文に欠落しているため個別検証はできないが、条件を満たさず、図2のようなE1/E2での明確な打ち切りは得られない。
不正解。一般に上限E1・下限E2の両側クリップでは、Vi>E1で上側ダイオードのみが導通しVo=E1、Vi<E2で下側ダイオードのみが導通しVo=E2となる必要がある。本選択肢の具体的接続は本文から読み取れないが、いずれかのしきい設定や極性が適合せず、図2の動作条件を満たさない。
不正解。図2のように上下をE1・E2で打ち切るには、2本のダイオードが互いに逆向きかつ各基準電圧と適切に接続されていなければならない。本文では回路詳細が欠落しているため個別の誤り箇所は特定できないが、条件不成立のため所望の波形は得られない。
正解。理想ダイオードを互いに逆向きに配置し、それぞれを基準電圧E1(上限)・E2(下限)に結ぶ両側クリップ回路。Vi>E1で上側ダイオードが導通しVoはE1にクランプ、Vi<E2で下側ダイオードが導通しVoはE2にクランプ、E2≦Vi≦E1では両ダイオードは遮断されVo≈Viとなる。理想ダイオードのため順方向降下は0 Vで、閾値がちょうどE1・E2になるので図2の出力が再現される。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。


解説
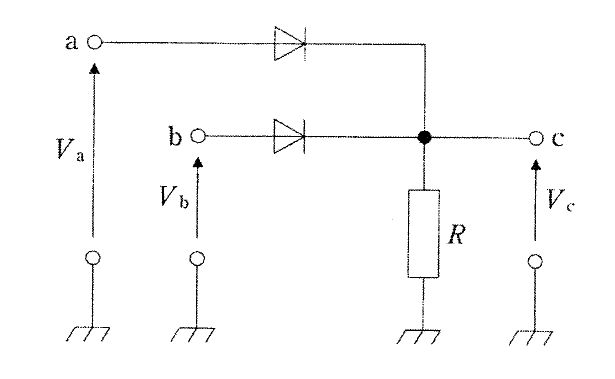
提示の回路は、入力a・bからそれぞれ理想ダイオードで合流し、合流点(出力c)が抵抗Rで接地に引かれている構成で、理想ダイオードの順方向電圧降下を0Vとみなすと、出力は入力の最大値に一致する($V_c=\max(V_a, V_b)$)。したがってVa,Vbがともに0Vのときのみダイオードは両方オフとなり、Rによってcは0Vに引き下げられる。いずれか一方でも5Vであれば、その側のダイオードが導通してcは5Vに引き上げられる。よって真理値表は(0,0)→0、(0,5)→5、(5,0)→5、(5,5)→5となる。
選択肢別解説
本回路(理想ダイオードOR)の正しい出力は、(0,0)→0、(0,5)→5、(5,0)→5、(5,5)→5である。選択肢1は(0,5)や(5,0)のときに0Vとしており、いずれかの入力が5Vであれば出力も5VになるというOR動作に反するため不適切。
理想ダイオードORでは(0,0)のみ0Vで、他は5Vとなる。選択肢2は(0,0)で5V、(5,5)で0Vとするなど、基準と逆転した行が含まれ、回路動作と一致しないため不適切。
本回路の正しい真理値表は(0,0)→0、他→5である。選択肢本文(数表)がDBでは欠落しており厳密な照合はできないが、問題の回路動作に合致しない表であるため不適切と判断する。
理想ダイオードORでは、いずれかの入力が5Vならダイオードが導通して出力cは5V、両方0VのときのみRで0Vとなる。選択肢4は(0,0)→0、(0,5)→5、(5,0)→5、(5,5)→5と示し、回路動作と一致するため適切。
選択肢5は(0,0)で5V、(0,5)や(5,0)で0Vとするなど、理想ダイオードORの動作(入力の最大値が出力に現れる)に反しているため不適切。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
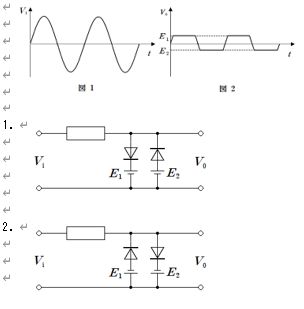
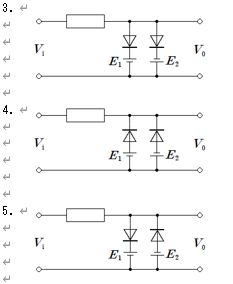
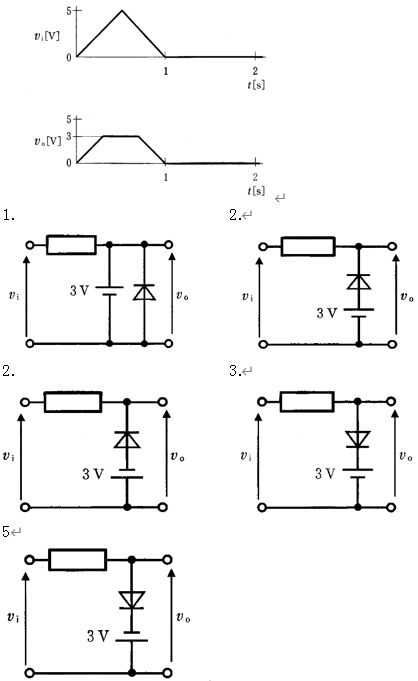
入力は0〜5Vの三角波で、出力は+3Vを上限に平坦化(クリップ)された波形である。理想ダイオードを用いた正側クリップ(シャント型)で実現でき、条件は「出力ノードの電位が+3Vを超えたらダイオードが順方向導通し、出力を+3Vに固定する」ことである。これを満たすのは、出力(=入力側ノード)をダイオードのアノード、+3V基準をカソードに接続したシャント回路で、vi≤3Vではダイオードは逆方向でオフとなりvo≈vi、vi>3Vでオンとなりvo≈3Vに張り付く。図の回路4がこの構成に一致する。
選択肢別解説
抵抗の後段に3V電源とダイオードが直列で挿入された形で、出力ノードと基準電圧間に直接のクランプ経路が形成されない。入力が3Vを超えても出力を+3Vに強制する動作が得られず、所望の正側クリップ波形にはならない。
シャント接続だが、ダイオードの向き・基準の取り方が+3Vでの正側クリップ条件を満たさない。出力が+3Vを超えてもダイオードが順方向になりにくく、所望の+3Vクランプは得られない(負側領域の抑制向きの構成)。
基準が−3V側となる負側クリップの構成で、viが−3V以下で導通して出力を−3V付近に制限するタイプ。+3Vでの正側クリップ波形には一致しない。
正側クリップ(シャント型)。出力ノード(入力側)をダイオードのアノード、+3V基準をカソードに接続。vi≤3Vではオフでvo≈vi、vi>3Vでオンとなりvoを+3Vに固定するため、図示の出力波形(上側が+3Vで平坦)を再現できる。
ダイオードの相手側が−3V基準となるシャント構成で、−3V付近での制限を生じる。+3Vで上側をクリップする目的には合致しない。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
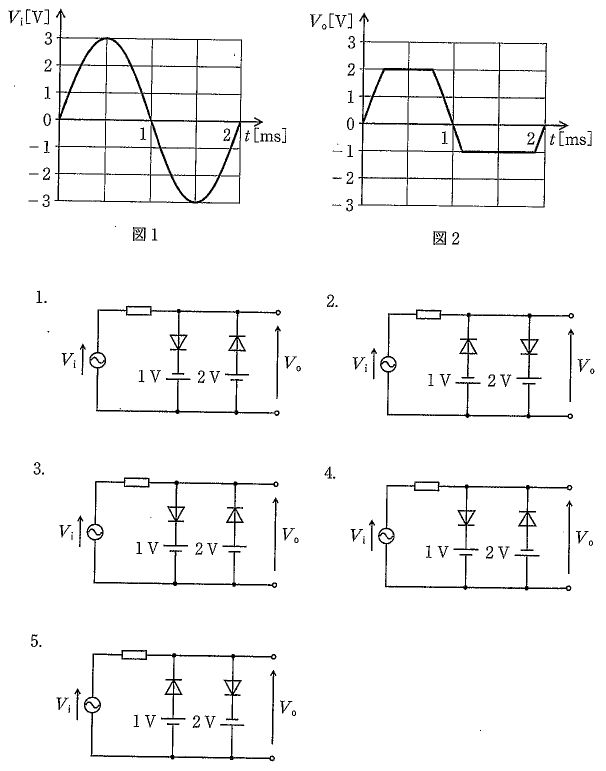
図2の出力波形は、入力が正方向に大きいときは +2 V で頭打ち、負方向に大きいときは −1 V で頭打ちになる両極性の並列リミッタ(クリッパ)である。理想ダイオードでは、Vo が +2 V を超えると「+2 V 基準側」のダイオードが導通し Vo は +2 V に保持され、Vo が −1 V 未満になると「−1 V 基準側」のダイオードが導通して Vo は −1 V に保持される。−1 V~+2 V の範囲では両ダイオードは遮断で、Vo は入力 Vi を抵抗経由でそのまま追従する。したがって回路としては、+2 V で上側クランプ、−1 V で下側クランプになるようにそれぞれのダイオードの向きと直流電源の極性を組み合わせたもの(選択肢2)が該当する。数式的には、理想動作は $V_o=\mathrm{clip}(V_i,-1,+2)$ と表せる。
選択肢別解説
1 V 側・2 V 側の極性とダイオードの向きの組合せが不適切で、負側のクリップが −1 V にならず(+1 V 側に張り付く構成)、図2の下側平坦部と一致しない。
+2 V 側の枝は Vo が +2 V を超えたときだけ導通し上限を +2 V に固定、1 V 側の枝は Vo が −1 V 未満で導通して下限を −1 V に固定する向き・極性となっている。−1 V~+2 V の間では両枝ともオフで Vi をそのまま出力するため、図2の波形(上限 +2 V、下限 −1 V のクリップ)を与える。
枝の向き/極性の対応が入れ違っており、上下限の設定が図2(+2 V と −1 V)にならない。結果として一方が +1 V、他方が −2 V のクリップとなり、所望の波形と不一致。
上側のクリップが +1 V、下側のクリップが −2 V になる組合せであり、図2の上限 +2 V・下限 −1 V とは一致しない。
上限が −1 V、下限が +2 V と極性が逆転するクリップとなる組合せで、図2の波形条件と矛盾する。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
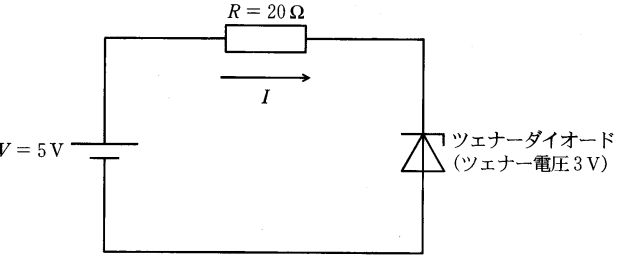
ツェナーダイオードは逆方向降伏時にツェナー電圧をほぼ一定(ここでは3 V)に保持する。図は電源5 V、抵抗R=20 Ω、ツェナーダイオードが直列であるため、電源電圧は抵抗の電圧降下VRとツェナー電圧VZの和になる。よって VR = 5 V − 3 V = 2 V。オームの法則より I = 2 V / 20 Ω = 0.1 A = 100 mA。したがって抵抗Rに流れる電流は100 mAである。
選択肢別解説
誤り。電源5 Vがツェナー電圧3 Vを上回るためツェナーダイオードは降伏状態とみなされ、直列回路に電流が流れる。I=0 mAにはならない。
正しい。直列関係からVR=5−3=2 V、オームの法則で I=2/20=0.1 A=100 mA。
誤り。計算上の電流は100 mAであり、150 mAにはならない。
誤り。計算上の電流は100 mAであり、250 mAではない。
誤り。計算上の電流は100 mAであり、400 mAではない。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
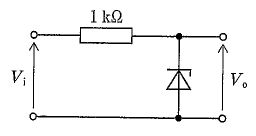
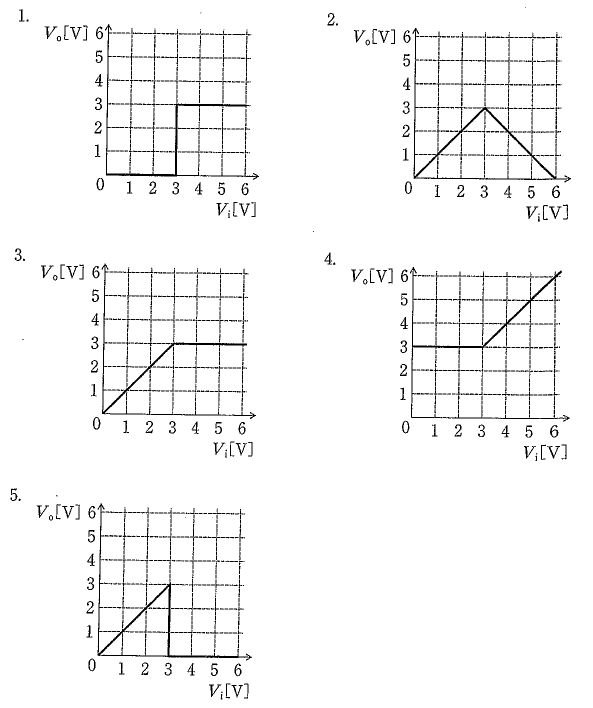
本回路は、入力Viから直列抵抗(1 kΩ)を介して出力ノードを駆動し、その出力ノードにツェナーダイオード(ツェナー電圧3 V)をシャント接続した定電圧クランプである。理想動作を仮定すると、Viが3 V未満ではツェナーダイオードは逆方向オフで電流が流れず、直列抵抗に電圧降下が生じないため出力はVo=Viとなる。Viが3 V以上になるとツェナー領域でダイオードが導通し、出力ノードはおおよそ3 Vにクランプされ、余剰の電圧は直列抵抗で吸収される。従って入出力特性は次の区分線形となる:$V_o=V_i\ (0\le V_i<3\ \text{V})$、$V_o\approx 3\ \text{V}\ (V_i\ge 3\ \text{V})$。この形(原点から傾き1で$V_i=3\ \text{V}$まで直線、以降$V_o=3\ \text{V}$の水平線)を示すグラフが正しい。設問の正答は選択肢3である。
選択肢別解説
不正解。ツェナー電圧が3 Vの本回路では、$V_i<3\ \text{V}$の範囲で$V_o=V_i$、$V_i\ge 3\ \text{V}$で$V_o\approx 3\ \text{V}$となる区分線形が正しい。選択肢1に対応するグラフはこの関係と一致しない(例えば$V_i<3\ \text{V}$で$V_o\ne V_i$や、$V_i\ge 3\ \text{V}$で$V_o$が一定にならない等)ため不適切である。なお、個別の線形状は画像が未提供のため確認できない。
不正解。本回路の正しい入出力関係は、$V_i<3\ \text{V}$で$V_o=V_i$、$V_i\ge 3\ \text{V}$で$V_o\approx 3\ \text{V}$である。選択肢2のグラフはこの特性と一致しない(折れ点電圧が3 Vでない、あるいは水平部が3 Vでない等のいずれか)ため不適切である。具体的な線形状は画像未提供のため特定できない。
正解。ツェナー電圧3 Vでクランプするシャント型の入出力特性を正しく表しており、$V_i<3\ \text{V}$では$V_o=V_i$の傾き1の直線、$V_i\ge 3\ \text{V}$では$V_o\approx 3\ \text{V}$の水平線となる。直列抵抗がツェナー電流を制限し、余剰電圧は抵抗にかかるため出力はほぼ一定に保たれる。
不正解。ツェナー素子は$V_i$がツェナー電圧に達するまではオフに近く、$V_o=V_i$となるのが正しい。選択肢4のグラフはこの前半の比例関係や、3 V以上での定電圧保持と一致しないため不適切である(例:$V_i<3\ \text{V}$から既に一定電圧とする等)。個別形状は画像未提供のため確認不可。
不正解。$V_i\ge 3\ \text{V}$で$V_o$は約3 Vにクランプされ、$V_i$の増加に伴って$V_o$が減少するようなグラフは本回路の物理に反する。直列抵抗により余剰電圧が吸収され、出力はほぼ一定となるため、この種の形状は不適切である。個別形状は画像未提供のため確認不可。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
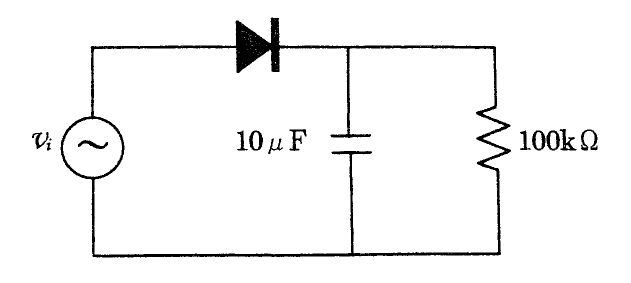
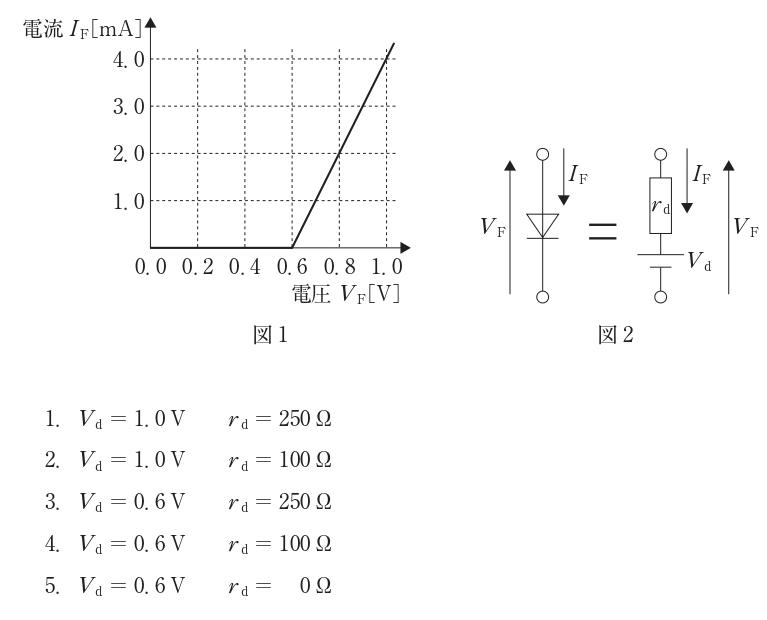
$図1の順方向I–V特性は、約0.6 Vで導通を開始し、その後はほぼ直線で増加している。図2の等価回路(直列の電圧源Vdと抵抗rd)で表すと、立ち上がり電圧はVd=0.6 Vとなる。直線部分の傾きから動抵抗rdを求めると、例えば(0.6 V, 0 mA)と(1.0 V, 4.0 mA)の2点より rd = ΔV/ΔI = 0.4 V / 4.0 \times 10^-3 A = 100 Ω となる。したがって正しい組合せは Vd=0.6 V、rd=100 Ω(選択肢4)。$
選択肢別解説
誤り。Vd=1.0 Vは図1の立ち上がり位置(約0.6 V)と一致しない。さらに、図1の直線の傾きから求まる動抵抗は約100 Ωであり、250 Ωではない。
誤り。動抵抗100 Ωは図1の傾きと整合するが、Vd=1.0 Vは立ち上がり電圧の読み取り(約0.6 V)と一致しない。
誤り。Vd=0.6 Vは妥当だが、図1の直線部分の傾きから rd = ΔV/ΔI ≈ 100 Ω であり、250 Ωではない。
正しい。図1より導通開始は約0.6 VでVd=0.6 V、また(0.6 V, 0 mA)→(1.0 V, 4.0 mA)から rd = 0.4/0.004 = 100 Ω と求まる。
誤り。rd=0 ΩならVd=0.6 V以上で電圧一定の垂直特性になるが、図1は有限の傾きを持つ直線でありrd≠0 である。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
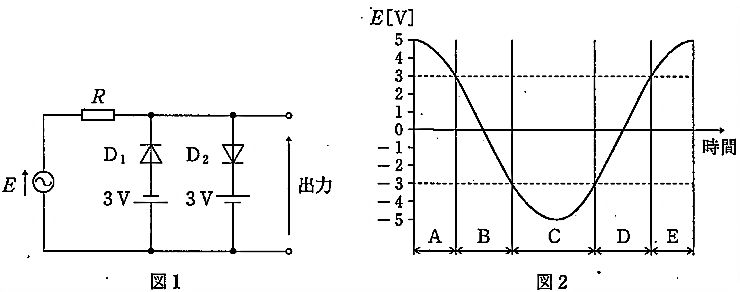
図1は ±3\text{ V} の直流電源を用いた両側(上下)リミッタ回路で、理想ダイオードを仮定する。入力ノード電圧が −3\text{ V} より低くなると、下側の枝(3\text{ V} 電源と直列のダイオード D1)が順方向となり電流が流れ、ノード電圧をおよそ −3\text{ V} にクランプする。逆に +3\text{ V} を超えると上側の枝(D2 側)が導通し、+3\text{ V} 付近にクランプされる。したがって D1 に電流が流れる条件は $E<-3\text{ V}$ のときであり、図2の波形でこの条件を満たすのは区間 C のみである。
選択肢別解説
区間Aでは $E>+3\text{ V}$。このとき順方向となるのは D2 側であり、D1 は逆方向で電流は流れない。
区間Bでは $-3\text{ V}\le E\le +3\text{ V}$。どちらのダイオードもオフで、D1 に電流は流れない。
区間Cでは $E<-3\text{ V}$。下側枝の D1 が順方向となり導通するため、D1 に電流が流れる。
区間Dでは $-3\text{ V}\le E\le +3\text{ V}$。両ダイオードともオフで、D1 に電流は流れない。
区間Eでは $E>+3\text{ V}$。導通するのは D2 であり、D1 は逆方向で電流は流れない。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
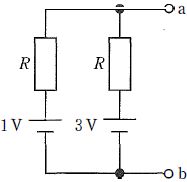
左右に同一抵抗 R と起電力 1 V・3 V の電源がそれぞれ直列で、上下ノード a と b の間に並列接続された回路である。a-b 間の電位差 V_ab は両枝で等しい。上向きを正として各枝の電流を I_1(左)、I_2(右)とおくと、各枝の端子電圧は V_{ab}=1-RI_1、V_{ab}=3-RI_2。ノード a には外部接続がないため KCL より I_1+I_2=0。よって 1-RI_1=3-R(-I_1)=3+RI_1 から -2RI_1=2 ⇒ RI_1=-1。これを代入して V_{ab}=1-(-1)=2 V。すなわち ab 間電圧は 2 V で、等抵抗の並列二枝に直列電源がある場合、端子電圧は起電力の平均 $(1+3)/2=2$ V となる。
選択肢別解説
$誤り。解析より V_{ab}=2\,V。1 V になるためには左右の電源 \cdot 抵抗条件が本問題と異なる必要がある。$
誤り。KCL と各枝の端子電圧関係より $1-RI_1=3-RI_2$、$I_1+I_2=0$ から $V_{ab}=2\,\text{V}$ が得られる。1.5 V にはならない。
正しい。KVL を単一ループに適用すると、起電力差 $3-1=2$ V が両抵抗の電圧降下 $2RI$ に等しくなるため $2=2RI\Rightarrow RI=1$。よって $V_{ab}=3-RI=3-1=2\,\text{V}$。
誤り。3 V は右枝電源の起電力であり、抵抗での電圧降下を考慮すると端子電圧は 3 V にはならない。
誤り。4 V は 1 V と 3 V の単純和だが、本回路は電源が並列二枝に分かれており、両抵抗での電圧降下・電流の釣り合いを満たすため端子電圧は 2 V となる。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
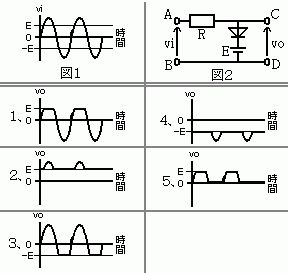
図2は直列抵抗Rで入力を受け、出力点(端子C)に理想ダイオードと直流電源Eが直列に接続されたバイアス付きクリッパ回路である。理想ダイオードを仮定すると、出力点の電位がEを超えようとした瞬間にダイオードが順方向導通し、出力はEにクランプされる。一方、出力点がE以下の範囲ではダイオードは逆バイアスで開放となり、Rに電流が流れないため出力は入力に等しくなる。従って出力は $v_o=\begin{cases}E & (v_i>E)\\ v_i & (v_i\le E)\end{cases}$ となり、正の側のみEで頭打ち(クリップ)され、負側は元の正弦波のまま残る波形(選択肢1)になる。
選択肢別解説
正しい。バイアスEを用いた正側クリッパ。$v_i>E$でダイオード導通により出力はEに固定、$v_i\le E$ではダイオード遮断で出力は入力に等しい。よって正のピークがEで水平に切り取られ、負の半周期はそのまま通過する。
誤り。正の半周期を0でクリップするには基準が0Vに対するクランプが必要だが、本回路はバイアス源Eを用いたクリップであり、クリップレベルはEである。
誤り。上側をEで、下側を0で同時にクリップするには追加の素子(逆向きダイオードや別基準)が必要。本回路は1個のダイオードと電源Eのみのため負側はクリップされない。
誤り。負側を−Eでクリップする動作は、ダイオードの極性を逆にした場合に相当する。本回路の極性では正側がEでクリップされる。
誤り。両側(±E)でのクリップは、左右対向のダイオード(またはツェナー等)を必要とする。図2は片側だけの構成なので該当しない。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
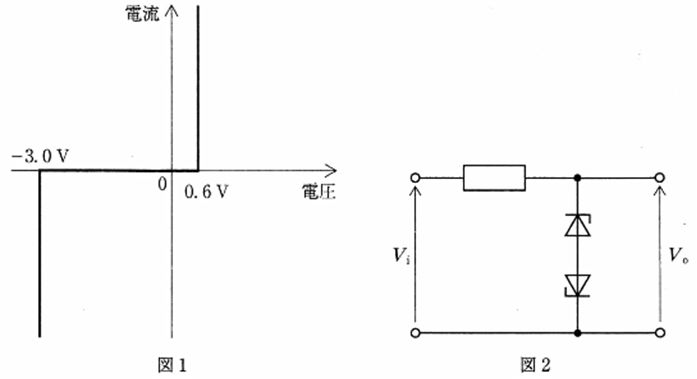
解説
図2は、ツェナーダイオード2個を向きを逆にして直列にし、出力端と基準(下側ノード)間に接続した両極性リミッタである。図1の特性より、順方向降下は約0.6 V、逆方向は$\lvert V_Z\rvert=3.0$ Vでツェナーブレークダウンする。正極性入力では一方が逆方向で$\lvert V_Z\rvert$に達し、他方が順方向に$0.6$ V導通するため、出力は $V_{o\max}=\lvert V_Z\rvert+V_F=3.0+0.6=3.6$ Vでクランプされる。負極性では役割が入れ替わり、$V_{o\min}=-(\lvert V_Z\rvert+V_F)=-(3.0+0.6)=-3.6$ Vとなる。よって最大・最小はそれぞれ$+3.6$ V、$-3.6$ V。
選択肢別解説
$\pm0.6$ Vでの制限は、通常ダイオードを逆並列で用いた場合の近似であり、本問のようにツェナー特性($\lvert V_Z\rvert=3.0$ V)を持つ場合は成り立たない。ツェナー電圧が関与するため不適。
正側が$0.6$ Vというのはツェナー電圧を無視しており誤り。正側・負側ともに$\lvert V_Z\rvert+V_F=3.6$ Vで対称にクランプされる。
$\pm3.0$ Vはツェナー電圧のみを考慮し、順方向降下$V_F=0.6$ Vを加味していないため誤り。実際は$3.0+0.6=3.6$ Vとなる。
正側は一方が逆方向ツェナー降伏($\lvert V_Z\rvert=3.0$ V)、他方が順方向導通($V_F=0.6$ V)となり、$V_{o\max}=3.6$ V。負側は対称に$V_{o\min}=-3.6$ V。問題文の前提と図1の特性に一致する。
$\pm6.0$ Vはツェナー電圧を2個分単純加算した誤解に基づく値。本回路では一方がツェナー降伏、他方は順方向導通であり、制限電圧は$\lvert V_Z\rvert+V_F=3.6$ Vである。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
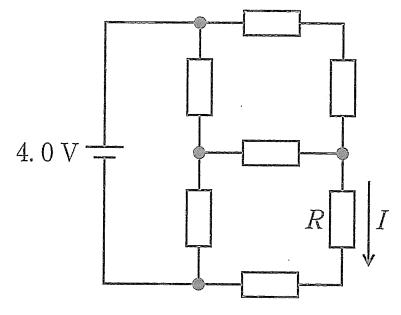
図の回路は全抵抗が 1.0 \Omega のブリッジ型で、上下の分割比が左右で等しいため中央の横抵抗には電流が流れない(ブリッジ平衡)。よって中央枝を除去して等価回路に置き換えると、左枝は直列 1.0+1.0=2.0 \Omega、右枝は上(1.0+1.0)と下(1.0+1.0)が直列で合計 4.0 \Omega となり、2.0 \Omega と 4.0 \Omega の並列で全合成抵抗は $R_{eq}=\left(\frac{1}{2}+\frac{1}{4}\right)^{-1}=\frac{4}{3}\,\Omega$。起電力 4.0 V から回路全電流は $I_{\text{total}}=\frac{4.0}{4/3}=3.0\,\mathrm{A}$。抵抗 R を含む右枝の電流は枝全抵抗 4.0 \Omega にかかる電圧 4.0 V を割れば $I=\frac{4.0}{4.0}=1.0\,\mathrm{A}$(あるいは分流の法則で 3.0\,A \times \frac{2}{2+4}=1.0\,A)。したがって求める電流は 1.0 A。
選択肢別解説
正しい。ブリッジ平衡により中央抵抗は無電流。左枝 2.0 \Omega と右枝 4.0 \Omega の並列から全電流 3.0 A、分流の法則で右枝(R を含む)に流れる電流は $3.0\times\frac{2}{2+4}=1.0\,\mathrm{A}$。同様に枝電圧 4.0 V、枝抵抗 4.0 \Omega から $I=1.0\,\mathrm{A}$ とも求まる。
$誤り。2.0 A であれば右枝の合計抵抗が 2.0 \Omega である必要があるが、右枝は 1.0+1.0+1.0+1.0=4.0 \Omega である。よって 4.0 V/4.0 \Omega=1.0 A。$
$誤り。3.0 A は並列合成(2.0 \Omega \parallel 4.0 \Omega=4/3 \Omega)に 4.0 V を加えたときの回路全電流であり、R を流れる枝電流ではない。$
$誤り。4.0 A を得るには対象枝が 1.0 \Omega である必要があるが、R を含む右枝は 4.0 \Omega であり、流れる電流は 1.0 A。$
誤り。5.0 A となるには全合成抵抗が 0.8 \Omega である必要があるが、実際の合成抵抗は $4/3\,\Omega$ と大きく矛盾する。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
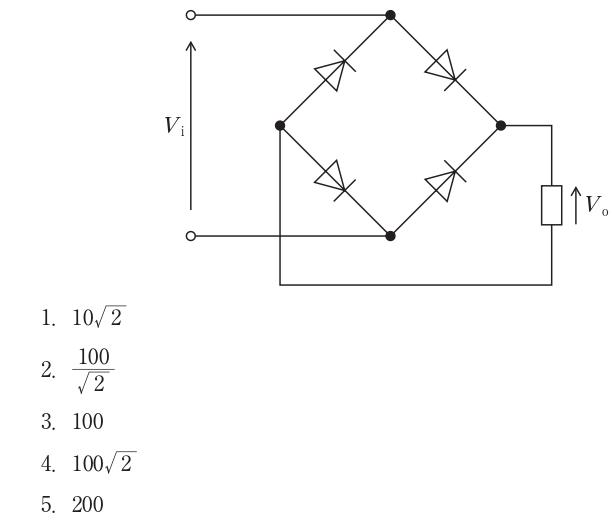
図はブリッジ型全波整流回路で、負半周期が反転され出力は $V_o=|V_i|$ となる。実効値は $V_{\mathrm{rms}}=\sqrt{\frac{1}{T}\int_0^T v^2(t)\,dt}$ で定義され、$|V_i|^2=V_i^2$ なので全波整流後の実効値は元の正弦波の実効値と等しい。入力 $V_i=100\sin(10\pi t)$ の最大値は $V_m=100\,\mathrm{V}$ であり、正弦波の実効値は $V_m/\sqrt{2}$。よって $V_o$ の実効値は $\frac{100}{\sqrt{2}}\,(\approx70.7\,\mathrm{V})$ となる。
選択肢別解説
誤り。$10\sqrt{2}\,\mathrm{V}\approx14.1\,\mathrm{V}$ であり、入力の最大値 $100\,\mathrm{V}$ から得られる全波整流出力の実効値にはならない。
正しい。全波整流では出力は $|100\sin(\omega t)|$。実効値は $\sqrt{\frac{1}{T}\int (100\sin(\omega t))^2 dt}=100/\sqrt{2}\,\mathrm{V}$。
誤り。$100\,\mathrm{V}$ は入力の最大値(ピーク値)であり、実効値ではない。
誤り。$100\sqrt{2}\,\mathrm{V}\approx141.4\,\mathrm{V}$ はピーク値を実効値と取り違えた値で、全波整流出力の実効値より大きすぎる。
誤り。$200\,\mathrm{V}$ はピーク・ツー・ピーク値($2V_m$)に相当し、実効値ではない。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
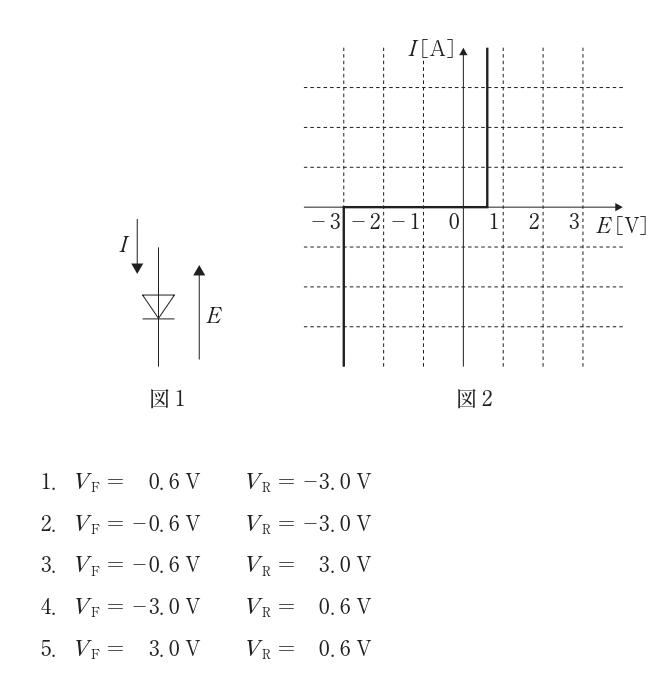
図1で電圧Eの正方向(右向き)・電流Iの正方向(下向き)が定義されている。図2のI–E特性では、E>0側で約0.6 V付近から電流が急増しており、これが順方向で導通を開始する電圧(順方向電圧VF)である。E<0側では−3.0 V付近で逆方向電流が急増しており、これが逆方向降伏(ブレークダウン)電圧VRである。したがってVF=0.6 V、VR=−3.0 Vが正しい。
選択肢別解説
正しい。図2より順方向(E>0)での立ち上がりは約+0.6 V、逆方向(E<0)でのブレークダウンは約−3.0 Vであるため、VF=0.6 V、VR=−3.0 Vとなる。
誤り。順方向電圧VFはE>0側で定義されるため正の値になる。図2では+0.6 Vで導通が始まるのでVFは+0.6 Vであり、−0.6 Vではない。VRの値(−3.0 V)は正しいが組合せとして不正解。
誤り。VFは+0.6 Vであり負ではない。またVRは−3.0 Vであり符号が逆になっている。
誤り。VFを−3.0 Vとしており値・符号とも不適切。−3.0 Vは逆方向降伏電圧VRである。さらにVRを+0.6 Vとしており、こちらも符号・値ともに誤り。
誤り。VFを+3.0 Vとする根拠はなく、図2の順方向しきいは+0.6 Vである。VRを+0.6 Vとしているが、降伏はE<0側の−3.0 Vで生じるため不一致。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
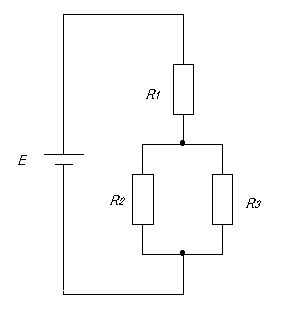
R1 が直列、R2 と R3 が並列の回路で、R2 の消費電力が 1 W、R2=4\Omega より、電力公式 $P=\frac{V^2}{R}$ から並列部の端子電圧は $V_{\parallel}=\sqrt{PR}=\sqrt{1\times4}=2\,\text{V}$。並列接続のため R3 の両端電圧も 2 V。よって $I_2=\frac{2}{4}=0.5\,\text{A}$、$I_3=\frac{2}{2}=1.0\,\text{A}$。キルヒホフの電流則より R1 を流れる電流は $I=I_2+I_3=1.5\,\text{A}$。オームの法則で R1 両端電圧は $V_{R1}=R_1 I=2\Omega\times1.5\,\text{A}=3\,\text{V}$。したがって答えは 3 V。
選択肢別解説
正しい。R2 の電力 1 W と R2=4\Omega から並列部電圧は 2 V。電流は $I_2=0.5\,\text{A}$、$I_3=1.0\,\text{A}$ で合計 $I=1.5\,\text{A}$。したがって $V_{R1}=2\Omega\times1.5\,\text{A}=3\,\text{V}$。
誤り。与条件から並列部電圧は 2 V で固定され、$I=1.5\,\text{A}$、$V_{R1}=3\,\text{V}$ と一意に定まる。5 V にはならない。
誤り。上記計算で $V_{R1}=3\,\text{V}$ と決まるため、7 V にはならない。
誤り。R2 の 1 W から導かれる並列部 2 V とオームの法則より、R1 の電圧は 3 V で一定。9 V にはならない。
誤り。同様に計算上 $V_{R1}=3\,\text{V}$ であり、11 V にはならない。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
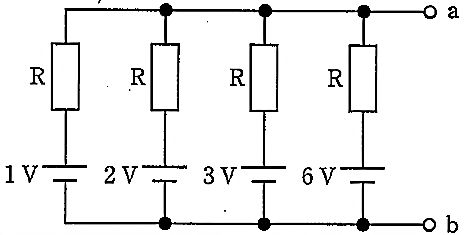
各枝は「理想電圧源 Vi と直列抵抗 R」からなる4本の並列回路で、端子abは外部負荷が接続されていない(開放)。節点aでKCLを立てると、各枝の抵抗を流れる電流は $(V_a - V_i)/R$ なので、$\sum (V_a - V_i)/R = 0$ より $V_a = \frac{\sum (V_i/R)}{\sum (1/R)}$ となる。全枝で抵抗は等しく R のため、$V_a = \frac{1+2+3+6}{4} = 3\,[\mathrm{V}]$。よって ab 間の電圧は 3 V。これは並列接続された複数のテブナン等価回路(同一内部抵抗)における合成起電力が、起電力の抵抗重み付き平均(同一 R なら単純平均)になることと一致する。
選択肢別解説
誤り。等しい内部抵抗Rをもつ4本の枝の起電力が 1, 2, 3, 6 V のとき、端子電圧は単純平均で 3 V。1 Vにはならない。
誤り。節点法より $V_{ab}=V_a=\frac{\sum (V_i/R)}{\sum (1/R)}=(1+2+3+6)/4=3\,\mathrm{V}$。2 Vではない。
正しい。全枝の内部抵抗が等しいため端子電圧は起電力の平均となり、$ (1+2+3+6)/4=3\,\mathrm{V} $。テブナンの定理での合成起電力の結果とも一致する。
誤り。最大の起電力 6 V に引きずられず、等抵抗並列では平均値 3 V となる。
誤り。12 V は起電力の単純和だが、内部抵抗を介して並列に接続されているため端子電圧は和にならず、平均の 3 V となる。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
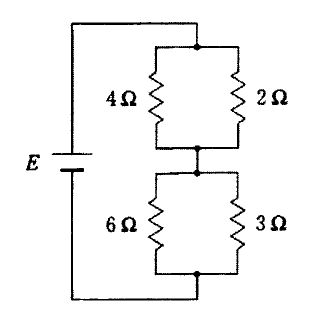
2Ω抵抗の消費電力が2Wより、この抵抗に流れる電流は $P=I^2R$ から $I=\sqrt{P/R}=\sqrt{2/2}=1\,\mathrm{A}$。よって上側並列(4Ωと2Ω)にかかる電圧は $V_a=IR=1\times2=2\,\mathrm{V}$。並列ゆえ4Ω枝の電流は $I_{4}=V_a/4=0.5\,\mathrm{A}$、上側を流れる総電流は $I_{\text{series}}=1+0.5=1.5\,\mathrm{A}$。この電流が下側並列(6Ωと3Ω)にも流れ、下側の合成抵抗は $R_b=(6\,\Omega\ \parallel\ 3\,\Omega)=2\,\Omega$。したがって下側の電圧は $V_b=I_{\text{series}}\,R_b=1.5\times2=3\,\mathrm{V}$。直列接続なので電源電圧は $E=V_a+V_b=2+3=5\,\mathrm{V}$。
選択肢別解説
誤り。2Vは上側の並列回路(4Ωと2Ω)にかかる電圧。2Ωの消費電力 $P=2\,\mathrm{W}$ から $I=\sqrt{P/R}=1\,\mathrm{A}$、よって $V=IR=2\,\mathrm{V}$。電源電圧は直列2段の和であり2Vではない。
誤り。3Vは下側の並列回路(6Ωと3Ω)にかかる電圧。上側を流れる総電流は $1+0.5=1.5\,\mathrm{A}$、下側の合成抵抗は $(6\parallel3)=2\,\Omega$ なので $V=1.5\times2=3\,\mathrm{V}$。電源電圧そのものではない。
誤り。4Vはこの回路のいずれの部位の電圧にも一致しない。直列2段の電圧和は $2\,\mathrm{V}+3\,\mathrm{V}=5\,\mathrm{V}$。
正しい。直列に接続された2つの並列回路の電圧和が電源電圧。上側が2V、下側が3Vのため $E=2+3=5\,\mathrm{V}$。
誤り。与えられた消費電力条件から導かれる電源電圧は $5\,\mathrm{V}$ であり、6Vにはならない。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。