臨床工学技士問題表示
臨床工学技士国家試験
解説
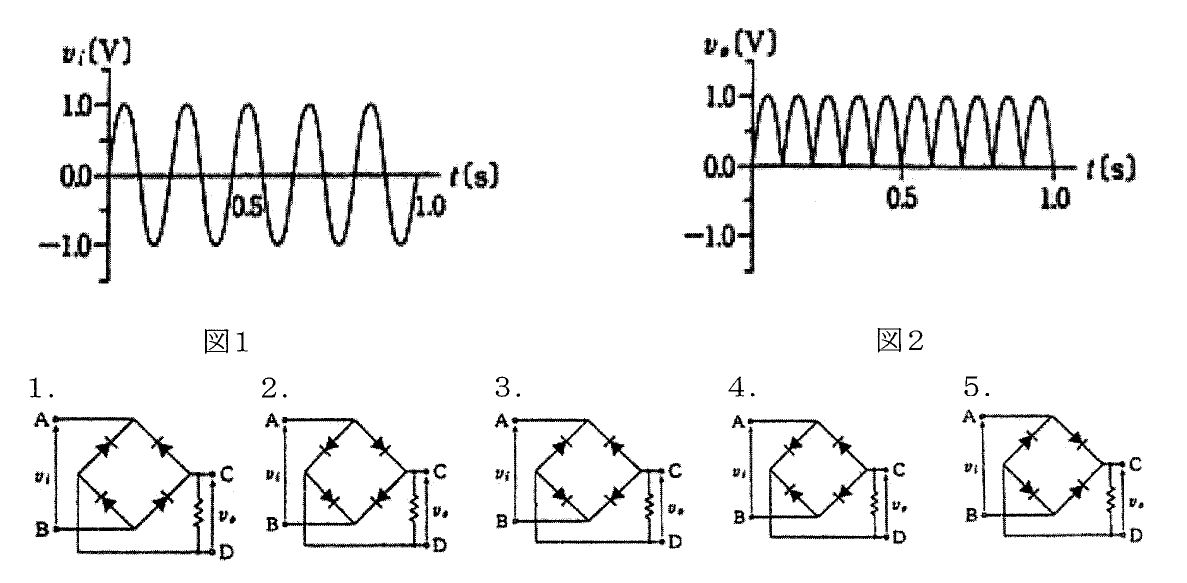
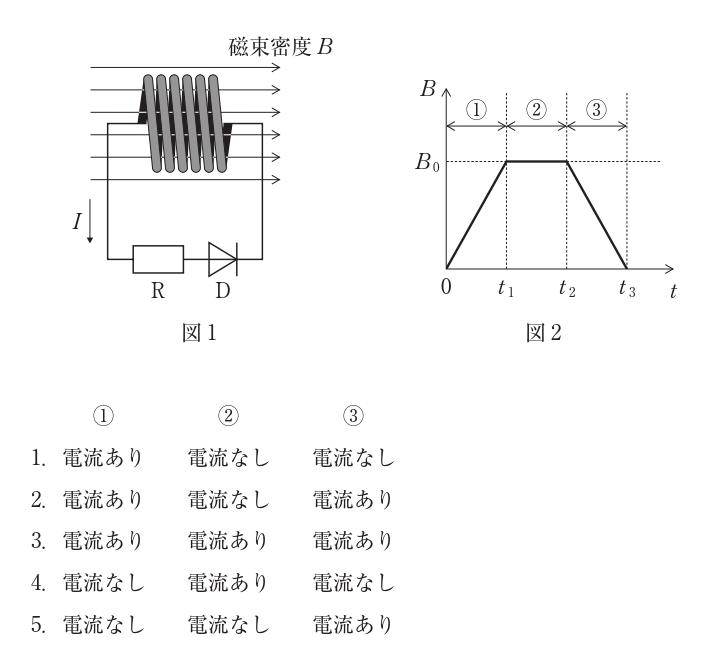
誘導起電力はファラデーの法則より $e=-N\,\frac{d\Phi}{dt}=-N\,S\,\frac{dB}{dt}$(一様磁界・コイル面積一定)で、符号はレンツの法則で決まる。図1の電流 I の向き(左枝を下向きの時計回り)がダイオード D の順方向である。①では B が増加($dB/dt>0$)するため、それを打ち消す向きの起電力が生じ、図示の I 方向(順方向)に電流が流れる。②では B 一定($dB/dt=0$)なので誘導起電力は 0、電流なし。③では B が減少($dB/dt<0$)し、①と逆向きの起電力が生じるが、その向きはダイオードを逆方向にバイアスするため電流は流れない。よって『① 電流あり、② 電流なし、③ 電流なし』が正しい。
選択肢別解説
正しい。①は $dB/dt>0$で順方向の誘導起電力が生じ電流あり。②は $dB/dt=0$で誘導起電力が 0、電流なし。③は $dB/dt<0$で起電力の極性が逆転しダイオードが逆方向となるため電流なし。
誤り。③では $dB/dt<0$ により起電力の向きが逆でダイオードが逆バイアスとなるため電流は流れない。
誤り。②は B 一定で $dB/dt=0$、誘導起電力が生じないため電流は流れない。
誤り。①では B 増加により順方向の誘導電流が流れるので『電流なし』は不適切。さらに②は $dB/dt=0$ で『電流あり』とはならない。
誤り。①は誘導起電力が順方向で電流が流れるため『電流なし』は不適切。③は逆バイアスで電流は流れないため『電流あり』は不適切。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
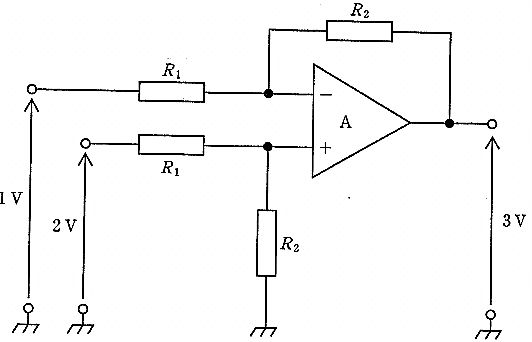
図は抵抗が左右対称に配置された差動増幅回路(減算回路)で、同名の抵抗 $R_1$ 同士、$R_2$ 同士は等しいと読む。理想OPアンプで負帰還が成立しているため $V_- = V_+$、入力電流は0とみなせる。非反転端子の節点電位は、2 Vと0 Vにそれぞれ $R_1$、$R_2$ で接続された2端子合成より $V_+ = \dfrac{\frac{2}{R_1}}{\frac{1}{R_1}+\frac{1}{R_2}}$。反転端子の節点電位は、1 Vと出力3 Vにそれぞれ $R_1$、$R_2$ で接続されているため $V_- = \dfrac{\frac{1}{R_1}+\frac{3}{R_2}}{\frac{1}{R_1}+\frac{1}{R_2}}$。$V_+=V_-$ より $\;2\left(\tfrac{1}{R_1}\right)=\left(\tfrac{1}{R_1}\right)+3\left(\tfrac{1}{R_2}\right)\;\Rightarrow\;\tfrac{1}{R_1}=3\tfrac{1}{R_2}\;\Rightarrow\;R_2=3R_1$。したがって比は $R_1:R_2=1:3$。同結果は、差動増幅器の標準式 $V_o=\dfrac{R_2}{R_1}(V_{+\text{側入力}}-V_{-\text{側入力}})$(本回路では $V_o=\dfrac{R_2}{R_1}(2-1)$)からも確認でき、$\dfrac{R_2}{R_1}=3$ が必要となる。
選択肢別解説
誤り。$R_1:R_2=2:1$ は $\tfrac{R_2}{R_1}=0.5$ を意味し、標準式 $V_o=\tfrac{R_2}{R_1}(2-1)$ に代入すると $0.5\,\text{V}$ となり、所与の 3 V を満たさない。
誤り。$R_1:R_2=1:2$ は $\tfrac{R_2}{R_1}=2$ で、$V_o=2\times(2-1)=2\,\text{V}$ にしかならず、3 V と一致しない。
正しい。$R_1:R_2=1:3$ すなわち $\tfrac{R_2}{R_1}=3$ とすると、$V_o=3\times(2-1)=3\,\text{V}$ で条件を満たす。節点方程式からも $R_2=3R_1$ が導かれる。
誤り。$R_1:R_2=1:4$ は $\tfrac{R_2}{R_1}=4$ で、$V_o=4\times(2-1)=4\,\text{V}$ となり不適。
誤り。$R_1:R_2=1:5$ は $\tfrac{R_2}{R_1}=5$ で、$V_o=5\times(2-1)=5\,\text{V}$ となり不適。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
LEDの発光強度は主として順方向電流に依存し、加えた電圧には比例しない。発光波長は半導体材料のバンドギャップで決まり、電流に比例して変化するものではない。一方、LEDは発光に必要なエネルギーギャップが大きいため順方向電圧は一般的なSi整流ダイオード(約0.6〜0.7 V)より高く、赤色で約1.8〜2.2 V、青・白色では3 V超となることが多い。フォトダイオードは入射光に応じた光電流を生じ、光起電力モードではアノードが正電位となり外部回路に対してアノード側から電流を供給する(アノードから流出)。したがって正しいのは3、4、5である。
選択肢別解説
誤り。LEDの発光強度は順方向に流れる電流に概ね比例して増減する。LEDのI–V特性は指数関数的で、加えた電圧と電流は比例しないため、発光強度も電圧には比例しない。さらに高電流域では温度上昇や効率ドロップで強度は飽和傾向を示す。
誤り。LEDの発光波長は半導体のバンドギャップ $E_{g}$ によりほぼ決まり、$E_{ph}=h c/\lambda$ の関係から電流で直接決まるものではない。電流を増やすと主に発光強度が増し、波長は接合温度上昇などでわずかにシフトする程度で比例関係にはならない。
正しい。一般的なSi整流ダイオードの順方向電圧は約0.6〜0.7 Vであるのに対し、LEDは光子放出に必要なエネルギーギャップが大きく、赤色でおよそ1.8〜2.2 V、緑〜青・白色では概ね2〜3 V超と高い。したがって整流用ダイオードよりLEDの順方向電圧は高い。
正しい。フォトダイオードを光起電力モード(無バイアス)で用いると、光照射によりアノードが正電位になり、外部回路に供給される出力電流はアノードから流出してカソード側へ向かう(外部回路視点でアノード→カソード方向)。フォトコンダクティブモード(逆バイアス)でも光電流の向きは同様である。
正しい。フォトダイオードでは入射光により生成されるキャリア数が光強度にほぼ比例するため、出力電流(光電流)は入射光が強くなると増加する。一般に $I_{ph}=R\,P_{in}$($R$: 応答度[A/W]、$P_{in}$: 入射光パワー[W])で表される動作範囲がある。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
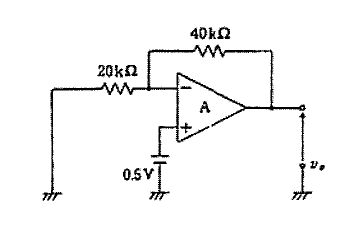
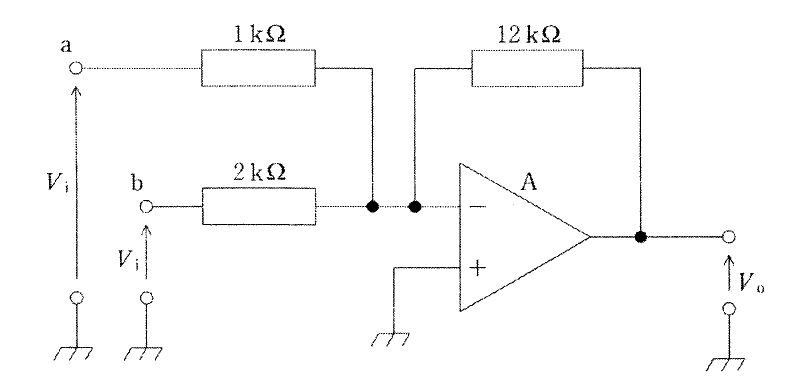
非反転端子(+)が接地された理想オペアンプの反転加算回路である。理想条件より仮想接地点が成立し、反転端子(−)の電位は0 Vとみなせる。各入力はそれぞれの入力抵抗を介してサミング点に流れ、帰還抵抗で電流和が出力に変換される。よって出力は $V_o=-\left(\frac{R_f}{R_{a}}V_i+\frac{R_f}{R_{b}}V_i\right)$。画像より $R_f=12\,\mathrm{k\Omega}$、$R_a=1\,\mathrm{k\Omega}$、$R_b=2\,\mathrm{k\Omega}$ なので、$V_o=-(12+6)V_i=-18V_i$。
選択肢別解説
誤り。反転加算回路の利得は $-(R_f/R_a + R_f/R_b)$。値を代入すると $-(12/1+12/2)=-18$ であり、$-2V_i$ にはならない。
誤り。等価利得は $-(12/1+12/2)=-18$。$-4V_i$ はいずれの単独入力経路の寄与とも一致しない。
誤り。$-6V_i$ は入力抵抗2 kΩ経路のみの寄与($-12/2=-6$)に相当し、1 kΩ側の寄与が無視されている。
誤り。$-12V_i$ は入力抵抗1 kΩ経路のみの寄与($-12/1=-12$)に相当し、2 kΩ側の寄与が欠落している。
正しい。反転加算回路より $V_o=-\left(\frac{12}{1}V_i+\frac{12}{2}V_i\right)=-(12+6)V_i=-18V_i$ となる。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
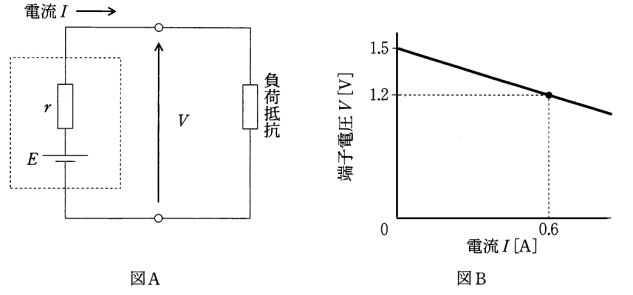
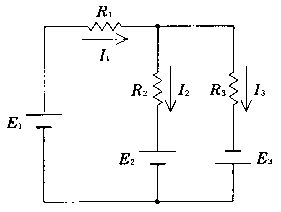
図Bの端子特性は直線で、電池の等価回路を前提に端子電圧と電流は V = E - rI の関係にある。図Bから I=0 A での切片は約 1.5 V なので起電力 E=1.5 V、さらに点 (I, V)=(0.6 A, 1.2 V) を用いると r=(E−V)/I=(1.5−1.2)/0.6=0.5 Ω。負荷抵抗 2.5 Ω を接続すると全抵抗は 2.5+0.5=3.0 Ω で、回路電流は I=E/(R+r)=1.5/3.0=0.5 A となる。したがって答えは 0.5 A。
選択肢別解説
誤り。図Bより E=1.5 V、r=0.5 Ω と読める。負荷 2.5 Ω 接続時の電流は I=E/(R+r)=1.5/(2.5+0.5)=1.5/3.0=0.5 A で、0.3 A にはならない。
誤り。電池の特性 V=E−rI、図Bの点 (0.6 A, 1.2 V) から r=0.5 Ω、E=1.5 V。したがって I=1.5/(2.5+0.5)=0.5 A で、0.4 A ではない。
正しい。図Bより E=1.5 V、r=0.5 Ω。負荷 2.5 Ω と直列なので全抵抗 3.0 Ω、I=1.5/3.0=0.5 A。
誤り。図Bから求めた E=1.5 V、r=0.5 Ω を用いると I=E/(R+r)=1.5/(2.5+0.5)=0.5 A。0.6 A にはならない。
誤り。図Bの直線から E=1.5 V、r=0.5 Ω。負荷 2.5 Ω のとき I=1.5/(2.5+0.5)=0.5 A で、0.7 A ではない。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
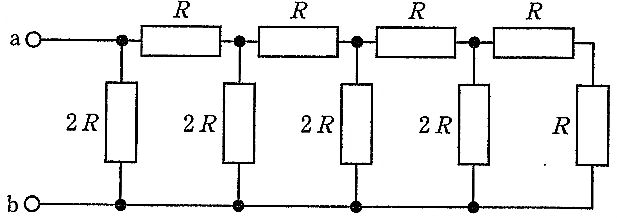
図の回路は、上側に直列のRが並び、各節点から下側母線(b)へ縦にシャント抵抗が接続されたラダー回路で、最右端だけシャントがR、それ以外は2Rとなっている。右端から順次合成すると、(1) 右端の横Rと縦Rは直列で2R、(2) これと左隣節点の縦2Rが並列で $R_p=\frac{2R\cdot 2R}{2R+2R}=R$、(3) 得られたRとその左の横Rが直列で2R、(4) これと次の縦2Rが並列で再びR…という操作を繰り返すと、入口(端子a)まで来たときの合成抵抗はRとなる。直列は $R_s=R_1+R_2$、並列は $R_p=\frac{R_1R_2}{R_1+R_2}$ を用いる。したがって端子ab間の合成抵抗はR。
選択肢別解説
ラダーを右端から順次簡約すると、各ステップで2R(直列)→R(並列)を繰り返し、入口ではRとなる。よって $\frac{1}{3}R$ は誤り。
同様に段ごとの合成で最終的にRに収束するため、 $\frac{1}{2}R$ は誤り。
右端の横Rと縦Rが直列で2R、これと左隣の縦2Rが並列でR、さらに左の横Rと直列で2R、次の縦2Rと並列でR…を繰り返すと、端子aから見た合成抵抗はRとなるため正しい。
段ごとの直列→並列の簡約を繰り返すと入口でRになる。2Rにはならないため誤り。
ラダー簡約の結果はRであり、3Rにはならないため誤り。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
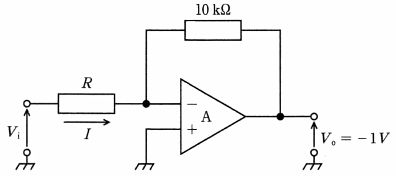
$回路は理想演算増幅器を用いた反転増幅回路で、非反転入力は接地のため反転入力端子は仮想短絡により約0 Vとなる。図より帰還抵抗は10 kΩ、出力は Vo = -1 V。したがって帰還抵抗に流れる電流は I_f = \frac{0 - (-1\,\text{V})}{10\,\text{k}\Omega} = \frac{1\,\text{V}}{10\,\text{k}\Omega} = 0.0001\,\text{A} = 0.1\,\text{mA}。節点電流の法則より入力抵抗 R を流れる電流も同じで I = 0.1 mA となる。設問で与えられた電圧増幅度20 dBは 20\log_{10}|A_v|=20 から |A_v|=10、反転より A_v=-10。A_v=-R_f/R より R=1 kΩ、さらに V_i=V_o/A_v=0.1 V、I=V_i/R=0.1 mA としても一致する。$
選択肢別解説
$0.01 mA (10 µA) は誤り。図より I = \frac{1\,\text{V}}{10\,\text{k}\Omega}=0.1\,\text{mA} となる。$
$正しい。理想OPアンプの仮想短絡より反転端は0 V、よって I = \frac{0-(-1\,\text{V})}{10\,\text{k}\Omega}=0.1\,\text{mA}。また 20 dB → |A_v|=10、A_v=-R_f/R から R=1 kΩ、I=V_i/R=0.1/1000=0.1 mA と一致。$
$1 mA は誤り。正しくは 0.1 mA。1 mA は正解の10倍で、R=1 kΩ \cdot V_i=0.1 V からは得られない。$
$10 mA は誤り。R=1 kΩ でも 10 mA を流すには 10 V が必要だが、図では V_i=0.1 V \cdot Vo=-1 V であり不整合。$
$100 mA は誤り。桁違いであり、与えられた Vo=-1 V \cdot R_f=10 kΩ からは I=0.1 mA が導かれる。$
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
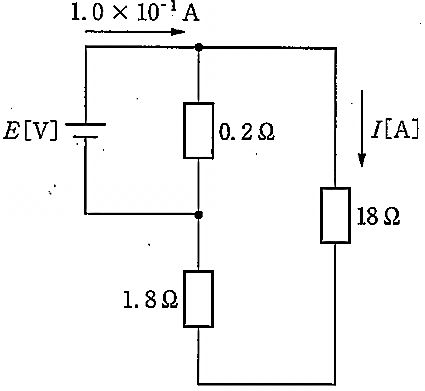
上部ノードで与えられている全電流は 1.0\times 10^{-1} A。図より、右枝の 18\,\Omega と左下の 1.8\,\Omega は直列で合成 19.8\,\Omega を形成し、これが 0.2\,\Omega の枝と並列になっている。求める 18\,\Omega を流れる電流 I は、19.8\,\Omega 枝を流れる電流に等しい。並列 2 枝における分流の法則より、枝 A の電流は $I_A = I_{\mathrm{total}}\,\frac{R_B}{R_A+R_B}$。ここで枝 A=19.8\,\Omega、枝 B=0.2\,\Omega、$I_{\mathrm{total}}=1.0\times 10^{-1}$ A として代入すると、$I = 0.1\times \frac{0.2}{19.8+0.2} = 0.1\times \frac{0.2}{20} = 1.0\times 10^{-3}$ A。したがって正答は 1。
選択肢別解説
正しい。18\,\Omega と 1.8\,\Omega の直列(19.8\,\Omega)と 0.2\,\Omega の並列で分流するため、$I = 0.1\times \frac{0.2}{19.8+0.2} = 1.0\times 10^{-3}$ A。
$誤り。約 9 mA は計算結果より約 9 倍大きい。並列二枝の抵抗比は 19.8:0.2=99:1 であり、19.8\,\Omega 枝の電流は全電流の約 1/100、すなわち約 1 mA になるべき。$
誤り。10 mA は分流比を無視した値で、正しくは約 1 mA ($1.0\times 10^{-3}$ A)。
$誤り。0.09 A は全電流 (0.1 A) に近すぎ、19.8\,\Omega 枝の電流として不適切。抵抗比から約 1/100 に分配されるため約 0.001 A が妥当。$
$誤り。1.0\times 10^{-1} A は図示の全体電流であり、並列分流後の 18\,\Omega を流れる枝電流ではない。$
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
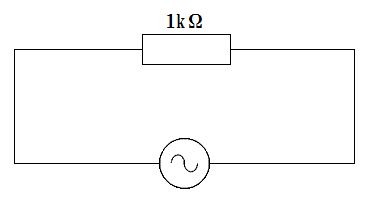
回路は1 kΩの純抵抗に正弦波交流電源が直列に接続されたものなので力率は1で、平均消費電力は実効値で計算する。与えられた最大値(波高値)$V_m=141\ \mathrm{V}$より、$V_{rms}=V_m/\sqrt{2}=141/\sqrt{2}\approx 99.7\ \mathrm{V}$。したがって消費電力は$P=V_{rms}^2/R\approx(99.7)^2/1000\approx 9.94\ \mathrm{W}$で、四捨五入して10 W。別解として$P=V_m^2/(2R)$でも同値となる。
選択肢別解説
誤り。計算では$P\approx 9.94\ \mathrm{W}$であり、7 Wにはならない。
正しい。$V_{rms}=141/\sqrt{2}\approx 100\ \mathrm{V}$、$R=1000\ \Omega$より$P=V_{rms}^2/R=100^2/1000=10\ \mathrm{W}$(厳密には約9.94 W)。
誤り。最大値を実効値と取り違えるなどの誤用でも14 Wにはならず、正しい計算結果は約9.94 Wである。
誤り。桁違い。純抵抗で$P=V_{rms}^2/R$より約10 Wであり、200 Wにはならない。
誤り。約10 Wが正しく、282 Wは物理的にもこの条件からは得られない。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
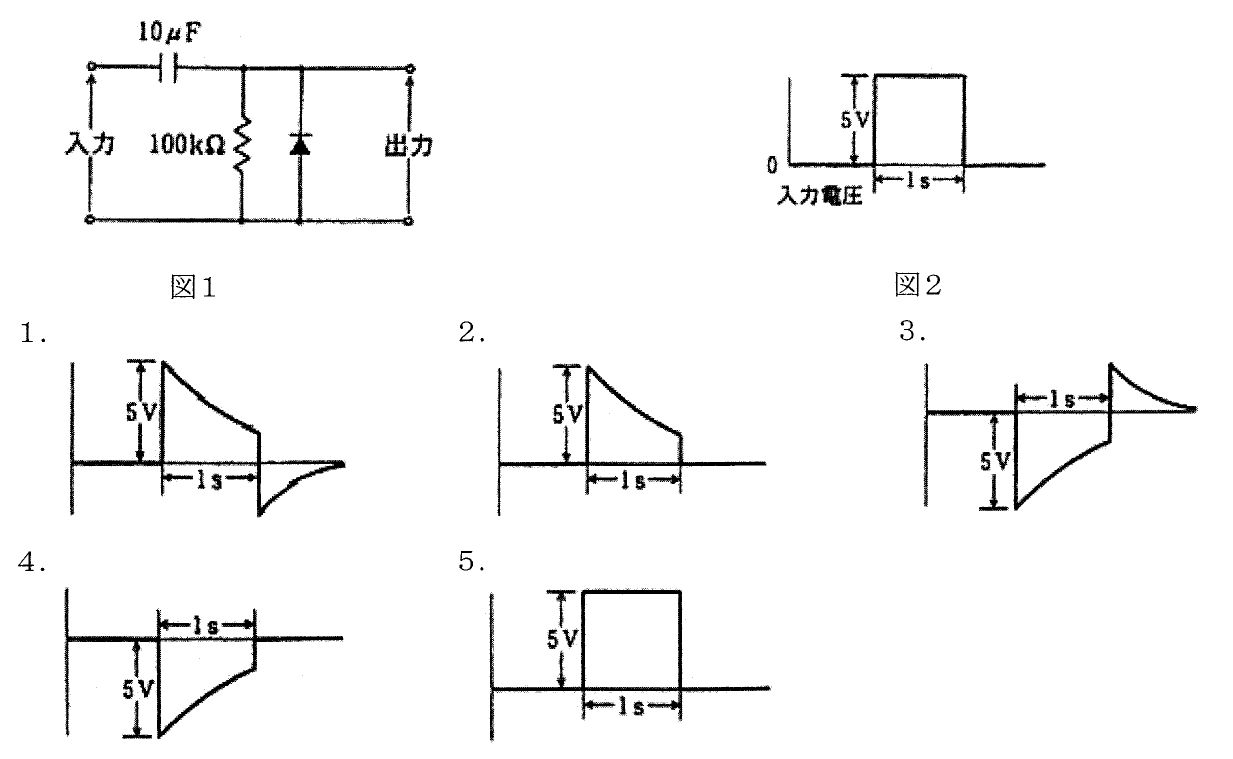
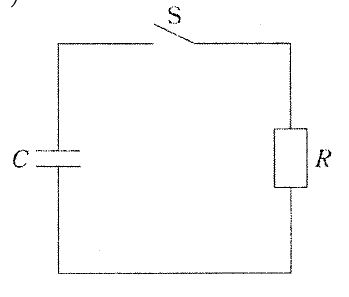
RC直列回路で、コンデンサ(初期電圧100 V)の放電をスイッチ閉成後に扱う。時定数は $\tau=CR=(10\,\mu\text{F})(50\,\text{k}\Omega)=0.5\,\text{s}$。放電電流は $i(t)=(V_0/R)\,e^{-t/\tau}$ で、抵抗電圧は $v_R(t)=i(t)R=V_0 e^{-t/\tau}$。よって $t=0.5\,\text{s}=\tau$ では $v_R=100\,e^{-1}$。与えられた近似 $e\approx 2.7$ を用いると $100/2.7\approx 37\,\text{V}$ で、選択肢3が最も近い。
選択肢別解説
63 Vは充電過程で $t=\tau$ にコンデンサ電圧が初期値の $1- e^{-1}\approx 63\%$ に達する値に対応する。放電での抵抗電圧は $V_0 e^{-t/\tau}$ であり、$t=\tau$ では約37 Vとなるため不適切。
時定数後に電圧が半分(50 V)になるわけではない。$v_R(t)=100 e^{-t/0.5}$ で50 Vを与えるのは $e^{-t/0.5}=0.5\Rightarrow t=\tau\ln 2\approx 0.35\,\text{s}$ の時であり、0.5 sではない。
放電時の抵抗電圧は $v_R(t)=100 e^{-t/0.5}$。$t=0.5\,\text{s}=\tau$ で $100 e^{-1}\approx 100/2.7\approx 37\,\text{V}$ となり、最も近い。
18 Vは $100 e^{-t/0.5}=18\Rightarrow t\approx 0.5\,\ln(100/18)\approx 0.86\,\text{s}$ で現れる値。0.5 sではないため不適切。
理想RC放電で電圧が0 Vになるのは $t\to\infty$ の極限。0.5 sでは0 Vにはならない。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
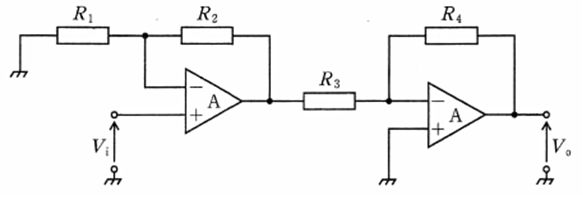
図より、1段目は非反転増幅回路(+端子に入力Vi、−端子にR1で接地基準、R2で帰還)、2段目は反転増幅回路(+端子は接地、−端子にR3で1段目出力を入力、R4で帰還)である。理想OPアンプの負帰還動作より、1段目の電圧利得は $A_{V1}=1+\frac{R_2}{R_1}$、2段目の電圧利得は $A_{V2}=-\frac{R_4}{R_3}$。多段回路の全体利得は各段利得の積となるため、$\dfrac{V_o}{V_i}=A_{V1}\,A_{V2}=\left(1+\frac{R_2}{R_1}\right)\left(-\frac{R_4}{R_3}\right)=-\left(1+\frac{R_2}{R_1}\right)\frac{R_4}{R_3}$ である。
選択肢別解説
正しい。1段目(非反転)の利得 $1+\frac{R_2}{R_1}$ と2段目(反転)の利得 $-\frac{R_4}{R_3}$ の積より、$-\left(1+\frac{R_2}{R_1}\right)\frac{R_4}{R_3}$ となる。
誤り。2段目が反転増幅のため全体利得には負号が付く。符号が正になっている点が不適切。
誤り。2段目は非反転ではなく反転増幅であり、利得は $-\frac{R_4}{R_3}$。したがって因子 $(1+\frac{R_4}{R_3})$ は不適切。
誤り。1段目の非反転増幅では利得は $1+\frac{R_2}{R_1}$ であり、$\frac{R_2}{R_1}$ のみではない。さらに全体は反転のため負号も必要。
誤り。1段目の利得は $1+\frac{R_2}{R_1}$ であり $\frac{R_2}{R_1}$ のみではない。また2段目は反転増幅で $(1+\frac{R_4}{R_3})$ ではなく $\frac{R_4}{R_3}$(負号付き)である。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
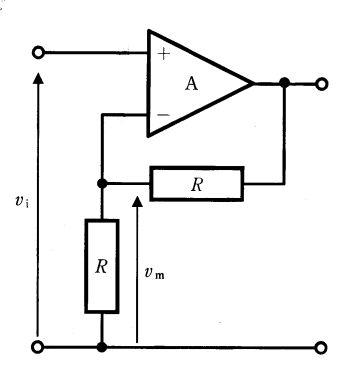
理想オペアンプを負帰還で用いると、入力差電圧は 0 V(仮想短絡)となり、反転入力端子電位 $v_-$ と非反転入力端子電位 $v_+$ は等しい。本回路では $v_+ = v_i$、反転入力端子の節点電位が $v_m$ なので $v_m = v_- = v_+ = v_i$ が成り立つ。さらに抵抗は $R_f=R_g=R$ の非反転増幅回路であり、$v_o = \left(1+\frac{R_f}{R_g}\right)v_i = 2v_i$、その分圧点である反転入力節点は $v_m = v_o\cdot\frac{R_g}{R_f+R_g} = 2v_i\cdot\frac{1}{2} = v_i$ と一致するため、選択肢4が正しい。
選択肢別解説
誤り。理想オペアンプの仮想短絡により $v_m=v_i$ であり、符号反転も2倍の関係も生じない。$v_m=-2v_i$ とはならない。
誤り。非反転入力に $v_i$ を与えた負帰還動作では $v_- = v_+ = v_i$ となるため、$v_m=-v_i$ にはならない。
誤り。$v_m$ は反転入力端子の電位で、一般には $v_i$ に等しい。$v_i=0$ の特殊な場合を除き $v_m=0$ ではない。
正しい。理想オペアンプの仮想短絡より $v_- = v_+ = v_i$、すなわち $v_m=v_i$。別法でも、$R_f=R_g=R$ の非反転増幅で $v_o=2v_i$、分圧点の $v_m=v_o/2=v_i$ と確認できる。
誤り。$2v_i$ となるのは出力電圧 $v_o$($v_o=2v_i$)であり、$v_m$ は分圧点かつ反転入力端子の電位で $v_m=v_i$。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。