臨床工学技士問題表示
臨床工学技士国家試験
解説
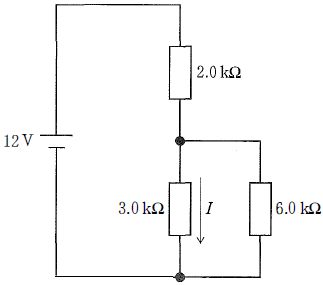
図では 3.0 k\Omega と 6.0 k\Omega が並列、これらの並列合成抵抗は $R_{\parallel}=\frac{3.0\times6.0}{3.0+6.0}=2.0\,\mathrm{k}\Omega$ となる。これが 2.0 k\Omega と直列なので全抵抗は $R_{\mathrm{tot}}=2.0+2.0=4.0\,\mathrm{k}\Omega$。電源電圧 12 V から回路電流は $I_{\mathrm{tot}}=\frac{12}{4.0\times10^3}=3.0\,\mathrm{mA}$。並列部にかかる電圧は $V_{\parallel}=I_{\mathrm{tot}}\times R_{\parallel}=3.0\,\mathrm{mA}\times2.0\,\mathrm{k}\Omega=6.0\,\mathrm{V}$(分圧でも同値)。したがって 3.0 k\Omega 抵抗の電流は $I=\frac{6.0}{3.0\times10^3}=2.0\,\mathrm{mA}$(下向き)。
選択肢別解説
$誤り。計算により 3.0 k\Omega を流れる電流は 2.0 mA。1 mA にはならない。$
誤り。並列部の電圧は 6.0 V であり、$I=\frac{6.0}{3.0\times10^3}=2.0\,\mathrm{mA}$。1.5 mA ではない。
正しい。3.0 k\Omega と 6.0 k\Omega の並列合成は 2.0 k\Omega、直列の全抵抗は 4.0 k\Omega。全電流は 3.0 mA、並列部の電圧は 6.0 V。よって 3.0 k\Omega の電流は $I=\frac{6.0}{3.0\times10^3}=2.0\,\mathrm{mA}$。
誤り。3 mA は回路全体を流れる電流 $I_{\mathrm{tot}}=\frac{12}{4.0\times10^3}$ であり、3.0 k\Omega 枝の電流ではない。
誤り。4.8 mA は並列合成抵抗を誤って 2.5 k\Omega と見積もったときの全電流 $\frac{12}{2.5\times10^3}$ に相当する可能性があるが、正しい並列合成は 2.0 k\Omega であり、3.0 k\Omega 枝の電流は 2.0 mA。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
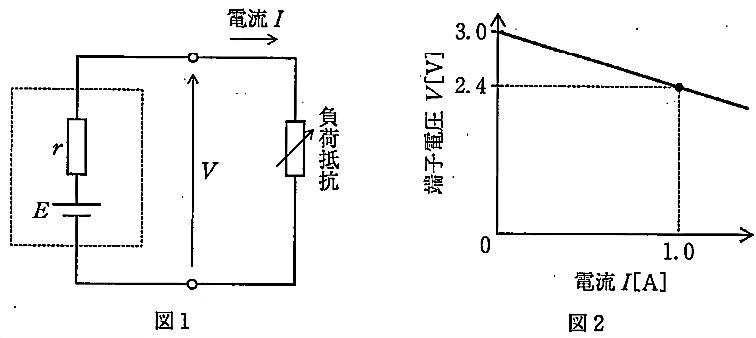
電池の端子電圧は内部抵抗による電圧降下を差し引いて $V=E-rI$ で表される。図2から、電流が 0 A のときの端子電圧は 3.0 V なので起電力 $E=3.0\,\text{V}$。さらに点 $(I,V)=(1.0\,\text{A},\,2.4\,\text{V})$ を用いると、$2.4=3.0-r\cdot1.0$ より内部抵抗は $r=0.6\,\Omega$。端子電圧が $V=2.7\,\text{V}$ のときは、$2.7=3.0-0.6I$ から $I=(3.0-2.7)/0.6=0.5\,\text{A}$。負荷抵抗はオームの法則より $R=V/I=2.7/0.5=5.4\,\Omega$。したがって正答は 5.4\,\Omega である。
選択肢別解説
R=3.6\,\Omega とすると I=V/R=2.7/3.6\approx0.75\,\text{A}。このときの端子電圧は式 $V=E-rI=3.0-0.6\times0.75=2.55\,\text{V}$ となり、与えられた 2.7 V と一致しないため不適。
R=4.2\,\Omega なら I=2.7/4.2\approx0.643\,\text{A}。$V=3.0-0.6\times0.643\approx2.61\,\text{V}$ で一致しないため不適。
R=4.8\,\Omega なら I=2.7/4.8=0.5625\,\text{A}。$V=3.0-0.6\times0.5625=2.6625\,\text{V}$ で 2.7 V と一致しないため不適。
図2から $E=3.0\,\text{V},\ r=0.6\,\Omega$。$V=2.7\,\text{V}$ のとき $I=(E-V)/r=(3.0-2.7)/0.6=0.5\,\text{A}$。よって $R=V/I=2.7/0.5=5.4\,\Omega$ で適切。
R=6.0\,\Omega とすると I=2.7/6.0=0.45\,\text{A}$。$V=3.0-0.6\times0.45=2.73\,\text{V}$ となり、条件の 2.7 V と一致しないため不適。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
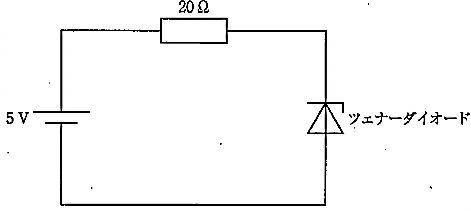
$ツェナーダイオードは逆方向で降伏すると両端電圧がツェナー電圧 V_Z にほぼ一定となる。図は電源 5 V、直列に 20 Ω 抵抗とツェナーダイオード(V_Z=3 V)が接続された回路であり、ダイオード両端は 3 V に保持される。よって抵抗にかかる電圧は V_R=5-3=2 V。オームの法則より抵抗電流は I=V_R/R=2/20=0.1 A=100 mA となる。$
選択肢別解説
0 mAではない。ツェナーダイオードが降伏して 3 V を保持し、残りの 2 V が 20 Ω にかかるため、I=2/20=0.1 A=100 mA が流れる。
正しい。ツェナー電圧 3 V、電源 5 V より抵抗電圧は 2 V。オームの法則で I=2/20=0.1 A=100 mA。
$150 mA なら抵抗電圧は V=I\times R=0.15\,\text{A}\times20\,\Omega=3 V となるが、本回路では抵抗にかかる電圧は 2 V(5-3)であり矛盾する。よって不正解。$
$250 mA なら抵抗電圧は 5 V となり、電源電圧 5 V 全てを抵抗で消費してしまうためツェナー側に電圧が残らず、前提(V_Z=3 V)と矛盾する。$
400 mA なら抵抗電圧は 8 V となり、そもそも電源電圧 5 V を超えて不可能。よって不正解。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
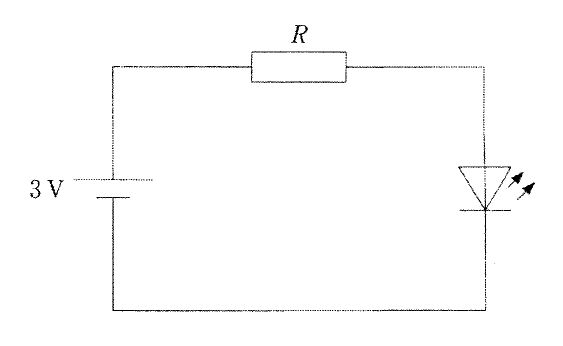
回路は電池・抵抗R・LEDの直列接続。直列回路では電源電圧は各素子の電圧降下の和に等しい(キルヒホッフの第2法則)。LEDの順方向電圧は 2 V と与えられているため、抵抗にかかる電圧は $V_R = V_S - V_D = 3-2 = 1\,\mathrm{V}$。流す電流は $I = 20\,\mathrm{mA} = 0.02\,\mathrm{A}$ なので、オームの法則より $R = \frac{V_R}{I} = \frac{1}{0.02} = 50\,\Omega$。従って抵抗値は50Ωが妥当。
選択肢別解説
0.05Ωでは $I = \frac{1\,\mathrm{V}}{0.05\,\Omega} = 20\,\mathrm{A}$ と極端に大きく、条件の20 mAにならないため不適切。
0.1Ωでは $I = \frac{1\,\mathrm{V}}{0.1\,\Omega} = 10\,\mathrm{A}$ となり、20 mAとかけ離れているため不適切。
正解。抵抗にかかる電圧は $1\,\mathrm{V}$、電流は $0.02\,\mathrm{A}$。よって $R = \frac{1}{0.02} = 50\,\Omega$。実務では標準系列から近い47Ωなどを用いる場合もあるが、条件値どおりなら50Ωが計算値。
100Ωでは $I = \frac{1\,\mathrm{V}}{100\,\Omega} = 10\,\mathrm{mA}$ と小さく、指定の20 mAにならない。しばしば $\frac{2\,\mathrm{V}}{0.02\,\mathrm{A}}=100\,\Omega$ とLEDを抵抗のように扱う誤りがあるが、LEDの順方向電圧はほぼ一定で線形抵抗ではない。
150Ωでは $I = \frac{1\,\mathrm{V}}{150\,\Omega} \approx 6.7\,\mathrm{mA}$ とさらに小さく、20 mAにならないため不適切。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
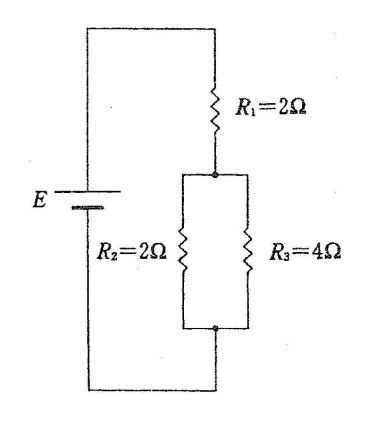
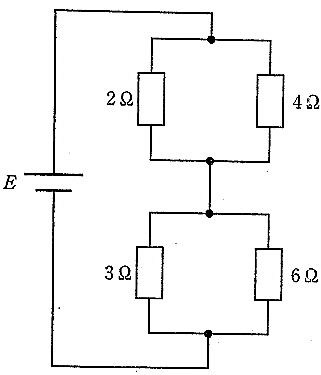
2Ω抵抗の消費電力が2Wより,上段の並列枝にかかる電圧を求める。消費電力は $P=V^2/R$ なので,$2=V_A^2/2$ から $V_A=2\,\text{V}$。上段の合成抵抗は $R_A=\frac{2\times 4}{2+4}=\frac{4}{3}\,\Omega$,下段の合成抵抗は $R_B=\frac{3\times 6}{3+6}=2\,\Omega$。直列接続のため電圧は抵抗比で分圧され,$R_A:R_B=\frac{4}{3}:2=2:3$。したがって下段の電圧は $V_B=V_A\times\frac{3}{2}=3\,\text{V}$。電源電圧は直列和 $E=V_A+V_B=2+3=5\,\text{V}$。
選択肢別解説
2 V は上段(2Ωと4Ωの並列枝)全体にかかる電圧 $V_A$ であり,電源電圧ではない。よって不正解。
3 V は下段(3Ωと6Ωの並列枝)にかかる電圧 $V_B$ であり,電源電圧ではない。よって不正解。
4 V は本回路の電源電圧とは一致しない。計算より $E=V_A+V_B=2+3=5\,\text{V}$。よって不正解。
正解。2Ω抵抗の消費電力2 Wから上段枝の電圧 $V_A=2\,\text{V}$。合成抵抗比 $R_A:R_B=2:3$ より下段電圧 $V_B=3\,\text{V}$,したがって電源電圧 $E=2+3=5\,\text{V}$。
6 V は本回路の結果と合わない。計算上 $E=5\,\text{V}$。よって不正解。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
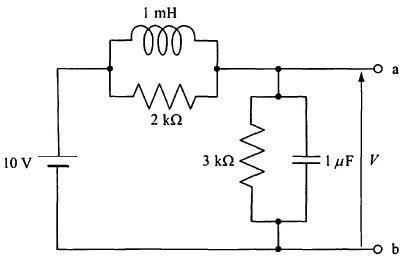
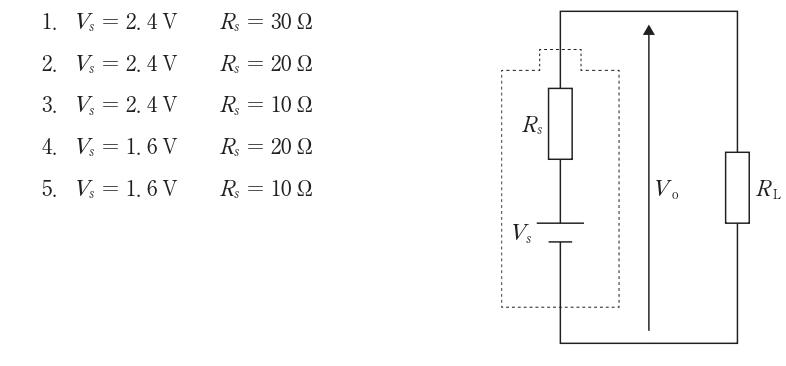
$電池をテブナン等価回路(起電力 Vs と内部抵抗 Rs)で表すと、負荷抵抗 RL に現れる端子電圧は V_o = V_s \frac{R_L}{R_s+R_L} で与えられる。与条件より 1.2 = V_s \frac{10}{R_s+10}、1.6 = V_s \frac{20}{R_s+20}。前式から V_s = 1.2\frac{R_s+10}{10} を後式に代入すると 1.6(R_s+20)=2.4(R_s+10) となり、R_s=10 \Omega。これを用いて V_s=1.2\frac{10+10}{10}=2.4 \t\text{ V}。よって組合せは Vs=2.4 V、Rs=10 \Omega が正しい。$
選択肢別解説
$候補: V_s=2.4 \t\text{ V}, R_s=30 \Omega。RL=10 \Omega のとき V_o=2.4\times\frac{10}{30+10}=0.6 \t\text{ V} で条件 1.2 V に一致しないため誤り。$
$候補: V_s=2.4 \t\text{ V}, R_s=20 \Omega。RL=10 \Omega で V_o=2.4\times\frac{10}{20+10}=0.8 \t\text{ V}、条件 1.2 V に一致しない。RL=20 \Omega でも 1.2 V となり条件 1.6 V に合わないため誤り。$
$候補: V_s=2.4 \t\text{ V}, R_s=10 \Omega。RL=10 \Omega で V_o=2.4\times\frac{10}{10+10}=1.2 \t\text{ V}、RL=20 \Omega で V_o=2.4\times\frac{20}{10+20}=1.6 \t\text{ V}。両条件を満たすため正しい。$
$候補: V_s=1.6 \t\text{ V}, R_s=20 \Omega。RL=20 \Omega で V_o=1.6\times\frac{20}{20+20}=0.8 \t\text{ V} と条件 1.6 V に一致しないため誤り。$
$候補: V_s=1.6 \t\text{ V}, R_s=10 \Omega。RL=10 \Omega で V_o=1.6\times\frac{10}{10+10}=0.8 \t\text{ V} と条件 1.2 V に一致しないため誤り。$
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
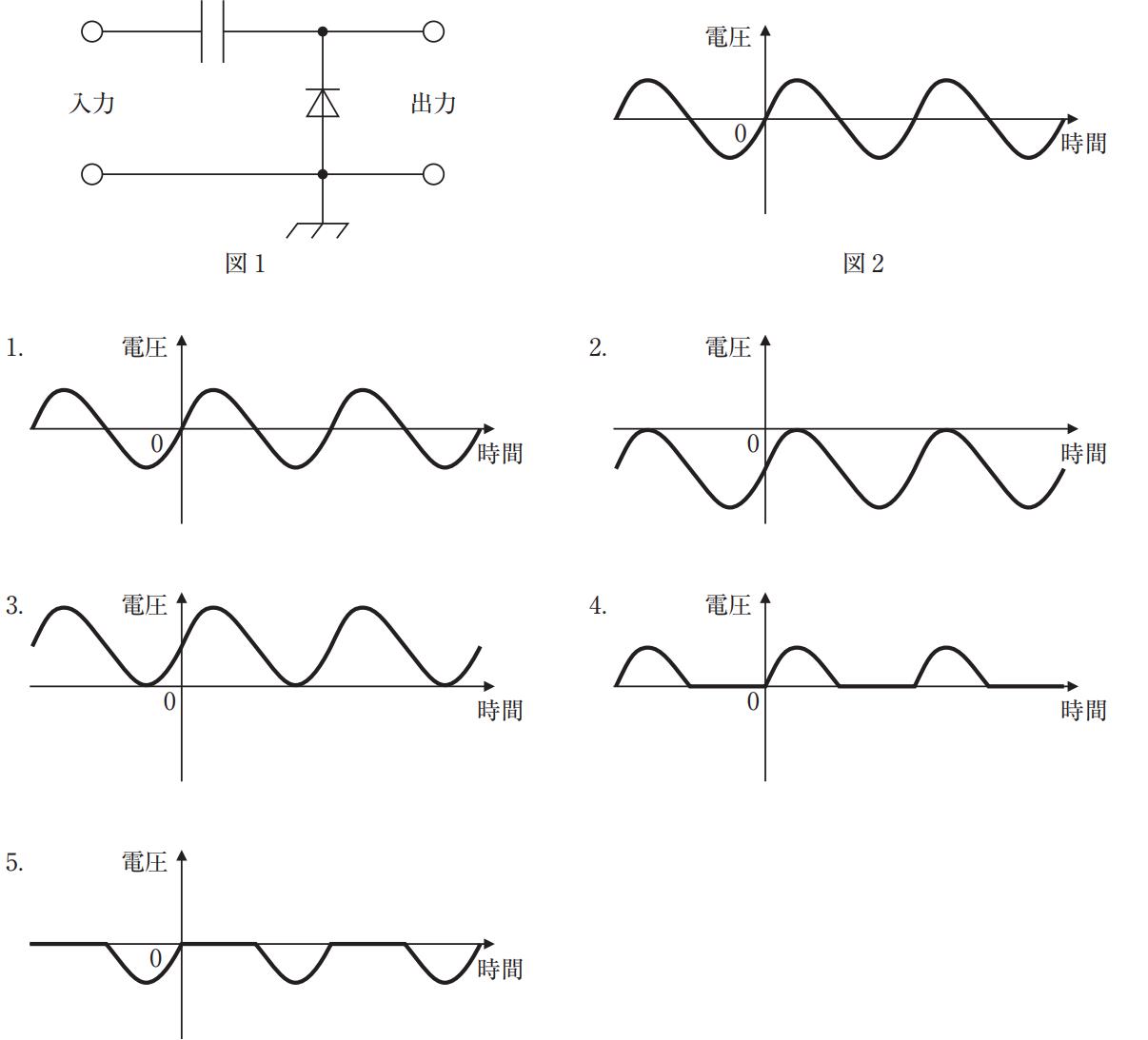
図1は入力と出力の間に直列コンデンサ、出力端を接地へ理想ダイオードでクランプする回路(正クランプ)である。入力が負ピーク($-E_m$)になるとダイオードが導通し、出力は0Vに固定され、そのときコンデンサには $E_m$ が充電される。以後、入力が増加してダイオードが逆方向となるとコンデンサ電圧は保持され(理想・大容量想定)、出力は $v_o=v_i+E_m$ となる。したがって波形全体が上方へ $E_m$ だけシフトし、最小値は0V、最大値は $2E_m$。選択肢の波形では3がこれに相当する。
選択肢別解説
図示の波形はシフトのない両極性正弦波(入力そのまま)に相当し、クランプ回路の出力にはならないため不適。正クランプでは波形全体が上方へシフトする。
下方に直流シフトしたような両極性波形(負クランプ相当)であり、本回路(正クランプ)の出力とは逆。ダイオードの向きから最小値が0Vに固定されるため不適。
波形全体が上方へシフトし、最小値が0V、最大値が $2E_m$ となる形で、正クランプ回路の出力と一致する。理想条件では $v_o=v_i+E_m$。
正半周期のみが出力される半波整流波形で、クリッピング回路の特性。クランプ回路は波形の振幅を変えず、基準電位をシフトさせるため不適。
負半周期のみが出力される半波整流波形であり、クランプ回路の出力ではない。振幅が半分になるような整流ではなく、クランプでは直流オフセットだけが付与される。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
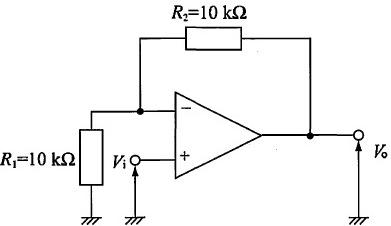
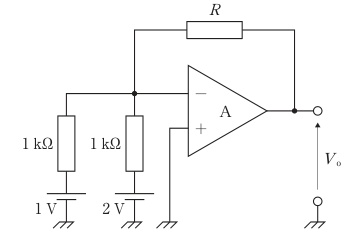
本回路は理想オペアンプを用いた反転加算回路である。非反転入力が接地のため仮想短絡により反転入力ノード電位は 0 V。理想オペアンプの入力電流は 0 とみなせるので、1 V と 2 V の各電源から 1 kΩ を介して反転入力ノードへ流れる電流はそれぞれ 1 mA、2 mA で合計 3 mA。この電流がすべて帰還抵抗 R を通って出力側へ流れる。ノードは 0 V、出力は −12 V なので R の両端電圧は 12 V。よってオームの法則より R = 12 V / 3 mA = 4 kΩ。一般式 $V_o=-R\left(\frac{V_1}{R_1}+\frac{V_2}{R_2}\right)$ に各値を代入しても $R=4\,\mathrm{k\Omega}$ が得られる。
選択肢別解説
R=2 kΩ とすると $V_o=-R\left(\frac{1}{1\,\mathrm{k\Omega}}\cdot1\,\mathrm{V}+\frac{1}{1\,\mathrm{k\Omega}}\cdot2\,\mathrm{V}\right)=-2\,\mathrm{k\Omega}\times3\,\mathrm{mA}=-6\,\mathrm{V}$ となり、−12 Vにならないため不適。
R=4 kΩ のとき、反転入力は仮想接地で 0 V、1 kΩ 経由で 1 V から 1 mA、2 V から 2 mA が流入し合計 3 mA。この電流が R を流れ、両端電圧は 12 V であるから $R=12\,\mathrm{V}/3\,\mathrm{mA}=4\,\mathrm{k\Omega}$。よって適切。
R=6 kΩ では $V_o=-6\,\mathrm{k\Omega}\times3\,\mathrm{mA}=-18\,\mathrm{V}$ となり、条件の −12 V と一致しないため不適。
R=8 kΩ では $V_o=-8\,\mathrm{k\Omega}\times3\,\mathrm{mA}=-24\,\mathrm{V}$ となり不適。
R=12 kΩ では $V_o=-12\,\mathrm{k\Omega}\times3\,\mathrm{mA}=-36\,\mathrm{V}$ となり不適。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
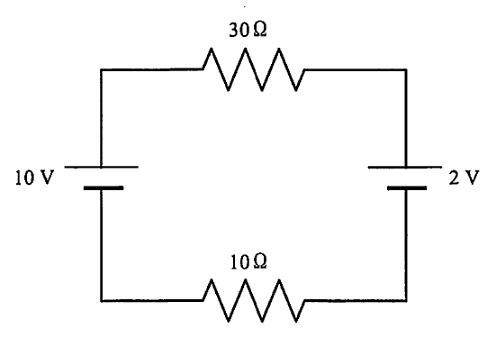
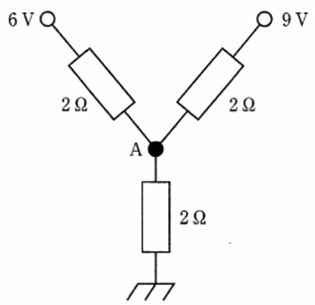
節点Aは3本の2\Omega抵抗で、左は6 V源、右は9 V源、下は接地(0 V)に接続されている。節点電圧法を適用し、電流の向きを節点Aから各枝へ流れる向きにとると、キルヒホッフの電流則より $(V_A-6)/2+(V_A-9)/2+(V_A-0)/2=0$。両辺に2を掛けて整理すると $3V_A-15=0$ となり、$V_A=5$ V。したがって最も近い値は5 Vである。
選択肢別解説
不適切。節点電圧法で $\frac{V_A-6}{2}+\frac{V_A-9}{2}+\frac{V_A-0}{2}=0$ を解くと $V_A=5$ V となるため、3 Vではない。
不適切。上式から $V_A=5$ V が導かれるため、4 Vではない。
適切。キルヒホッフの電流則より $\frac{V_A-6}{2}+\frac{V_A-9}{2}+\frac{V_A}{2}=0 \Rightarrow 3V_A-15=0 \Rightarrow V_A=5$ V。
不適切。節点電圧法の計算結果は $V_A=5$ V であり、6 Vではない。
不適切。節点電圧法の計算結果は $V_A=5$ V であり、7 Vではない。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
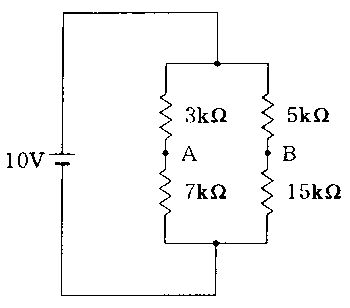
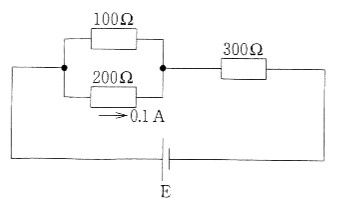
図の回路は、電源Eに対して「(100Ω // 200Ω) と 300Ωの直列」である。200Ω枝に0.1 Aが流れるので、並列部の端子電圧はオームの法則 $V=RI$ より $V_{\text{par}}=200\,\Omega\times 0.1\,\text{A}=20\,\text{V}$。並列なので100Ωの両端も20 V、よって100Ω枝の電流は $20\,\text{V}/100\,\Omega=0.2\,\text{A}$。合流後、300Ωを流れる電流は $0.1+0.2=0.3\,\text{A}$ となり、その電圧降下は $300\,\Omega\times 0.3\,\text{A}=90\,\text{V}$。キルヒホッフの第2法則(電圧則)より電源電圧は $E=V_{\text{par}}+V_{300}=20+90=110\,\text{V}$。
選択肢別解説
20 Vは並列部(100Ωと200Ωの両端)の電圧降下であり、回路全体の電源電圧ではない。Eはこの20 Vに直列の300Ωで生じる90 Vを加えた値になる。
50 Vは、誤って300Ωにも0.1 Aが流れると仮定して $300\,\Omega\times 0.1\,\text{A}=30\,\text{V}$ とし、並列部20 Vと加算した誤答と考えられる。実際の300Ω電流は合流後の0.3 Aであり、Eは110 Vとなる。
計算上の正解は110 V。もしE=70 Vとすると、300Ωの電圧降下は $70-20=50\,\text{V}$ となり、対応する電流は $50/300\,\Omega\approx 0.167\,\text{A}$ と分岐電流の和(0.1 A + 0.2 A = 0.3 A)と整合しないため誤り。
90 Vは300Ωの電圧降下($300\,\Omega\times 0.3\,\text{A}=90\,\text{V}$)のみを示す値であり、並列部の20 Vを加えていないため電源電圧Eとしては不足。
正しい。並列部の電圧降下20 Vと、直列の300Ωでの降下90 Vをキルヒホッフの第2法則で加算し $E=20+90=110\,\text{V}$ となる。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
ダイオードはpn接合の一方向素子で、アノードがカソードより高電位(順方向バイアス)のときに順方向電流が流れる。逆方向ではごく微小な漏れ電流のみで、ある電圧を超えると逆方向電流が急増する。この電圧を降伏電圧(ブレークダウン電圧)という。ダイオードは一方向性により整流作用をもち、交流を直流に変換する基本素子である。理想ダイオードでは順方向抵抗は0Ω、逆方向抵抗は無限大とみなす。
選択肢別解説
誤り。順方向電流はアノードがカソードより高電位のときに流れる。記述は極性が逆で、カソードを高電位にすると逆方向バイアスとなり、原則として電流は流れない(漏れ電流を除く)。
誤り。ダイオードは逆方向にはほとんど電流を流さないため、逆方向抵抗は順方向抵抗よりはるかに大きい(理想では無限大)。記述は関係が逆。
正しい。逆方向に印加した電圧を増やしていくと、ある電圧で逆方向電流が急激に増加する。この電圧を降伏電圧(ブレークダウン電圧)という(物理機構としてツェナー効果やアバランシェ効果がある)。定格内で用いる限り必ずしも破壊を意味しない。
正しい。ダイオードは一方向にのみ電流を通す性質を利用して整流に用いられる(半波整流・全波整流など)。
$誤り。理想ダイオードでは順方向抵抗は0\Omega、逆方向抵抗が無限大である。記述は逆の内容になっている。$
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
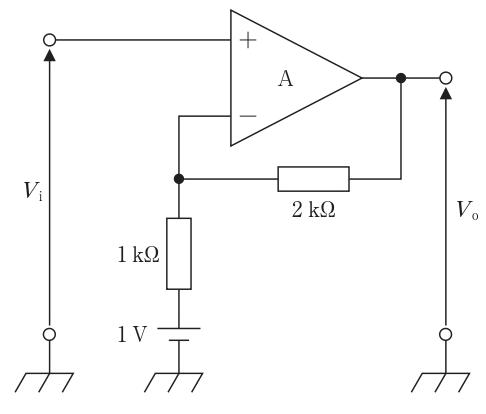
非反転入力に $V_i$ を与え、反転入力側には $R_1=1\text{k}\Omega$ の下端に基準電圧源 $E=1\text{V}$ を直列、出力から反転入力へ $R_2=2\text{k}\Omega$ の負帰還がかかる回路である。理想演算増幅器の仮定より入力電流は0、かつイマジナリーショートから $V_- = V_+ = V_i$。反転入力ノード電位を $V_a(=V_i)$ とし、KCLより $(V_a-E)/R_1 + (V_a - V_o)/R_2 = 0$。整理して $V_o = \left(1+\frac{R_2}{R_1}\right)V_i - \frac{R_2}{R_1}E$。数値代入で $V_o = (1+2/1)\times 3 - (2/1)\times 1 = 9 - 2 = 7\,\text{V}$。したがって正答は7。
選択肢別解説
誤り。計算式 $V_o = \left(1+\frac{R_2}{R_1}\right)V_i - \frac{R_2}{R_1}E$ に $R_1=1\text{k}\Omega, R_2=2\text{k}\Omega, V_i=3\text{V}, E=1\text{V}$ を代入すると $V_o=7\text{V}$ となるため 1 V にはならない。
誤り。非反転増幅のゲインは $1+R_2/R_1=3$ であり、基準電圧の影響を含めても $V_o=7\text{V}$ となる。入力と同じ 3 V にはならない。
誤り。KCLにより $(V_i-1)/1\text{k}\Omega + (V_i - V_o)/2\text{k}\Omega=0$ を満たす必要があり、これを解くと $V_o=7\text{V}$。5 V にはならない。
正しい。理想OPアンプのイマジナリーショートより $V_-=V_+=V_i=3\text{V}$。KCLから $V_o=3V_i-2E=3\times 3-2\times 1=7\text{V}$。
誤り。9 V は基準電圧源が無い理想的な非反転増幅(ゲイン3)のみを考えた値。実際は基準電圧 $E=1\text{V}$ により $\frac{R_2}{R_1}E=2\text{V}$ 分だけオフセットされ、$V_o=7\text{V}$ となる。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
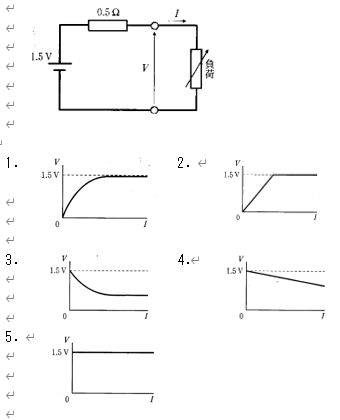
内部抵抗rをもつ理想電圧源Eの端子電圧は、内部抵抗での電圧降下rIを差し引いた $V=E-rI$ で与えられる。本問ではE=1.5 V、r=0.5 Ωより $V=1.5-0.5I$。よってI=0(無負荷)でV=1.5 V、Iが増えるほどVは傾き−0.5 V/Aの直線で減少し、短絡時には $I=E/r=1.5/0.5=3$ AでV=0となる。この特性に一致するのは直線的に1.5 Vから右下がりとなるグラフ(選択肢4)。
選択肢別解説
I増加とともにVが非線形に上昇して1.5 Vに漸近する形は、内部抵抗による電圧降下を説明できない。内部抵抗r=0.5 Ωがあるため $V=E-rI$ でVは減少するので不適切。
Iの増加でVが線形に増加し、その後1.5 Vで一定となる形は、内部抵抗をもつ電源の関係 $V=E-rI$(負の傾き)と逆の挙動であり不適切。
Iの増加でVが1.5 Vから非線形に減少する形は、減少方向は合うが内部抵抗モデルでは $V=E-rI$ と線形関係であるため不適切。
Iの増加に対しVが1.5 Vから傾き−0.5の直線で減少する。式 $V=1.5-0.5I$ に一致し、I=0でV=1.5 V、I=3 AでV=0となるため正しい。
Vが常に1.5 Vで一定なのは内部抵抗が0の場合。r=0.5 Ωでは $V=E-rI$ によりIとともにVは低下するため不適切。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
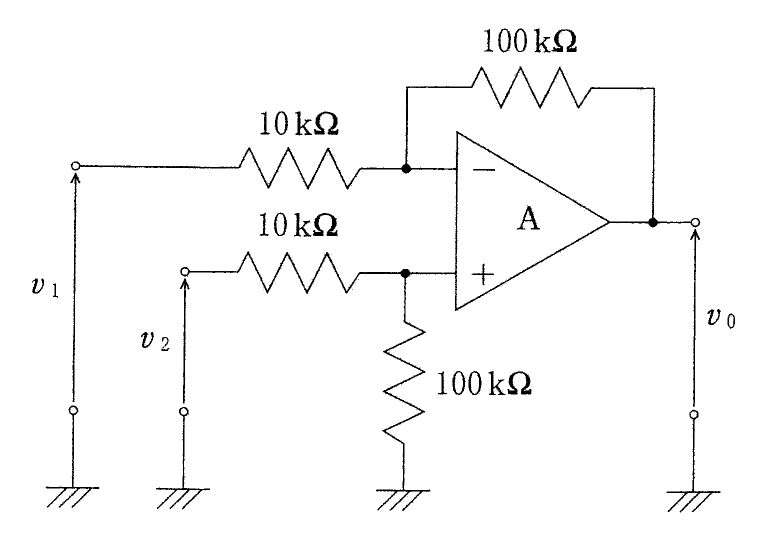
$図は4抵抗型の差動増幅器(減算器)。抵抗は R1=10 kΩ(v1→-端子),R2=100 kΩ(帰還),R3=10 kΩ(v2→+端子),R4=100 kΩ(+端子→接地)。画像より R2/R1=R4/R3=10 が成り立つため,理想OPアンプの減算器の一般式 v0=(R2/R1)(v2-v1) がそのまま適用できる。よって v0=10 \times (0.3-0.1)=+2 V。符号が正になるのは,v2(+端子側)が v1 より高く,差動利得が正だからである。参考として一般導出は,v+=\frac{R_4}{R_3+R_4}v2,v0=(1+R2/R1)v+-(R2/R1)v1。ここに R2/R1=R4/R3 を代入すると v0=(R2/R1)(v2-v1) に一致する。$
選択肢別解説
-2 Vは誤り。差動利得は R2/R1=10,v2−v1=0.2 V なので v0=10×0.2=+2 V となり,符号も正である。
-1 Vは誤り。計算上は v0=10×(0.3−0.1)=+2 V。負号にもならない。
0 Vは誤り。入力差 v2−v1=0.2 V が非零であり,利得10により +2 V が得られる。
+1 Vは誤り。差動利得10を掛けるため +0.2 V は +2 V に増幅される。
+2 Vが正しい。R2/R1=R4/R3=10 の減算器より v0=(R2/R1)(v2−v1)=10×(0.3−0.1)=+2 V。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
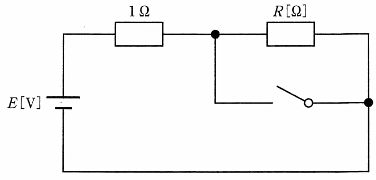
$スイッチOFF時は電源E[V]—1Ω—R[Ω]が直列で、1Ωに流れる電流(回路電流)は I_off = \frac{E}{1+R}。スイッチONでRがスイッチにより短絡(バイパス)され、1Ωのみとなるため I_on = \frac{E}{1} = E。条件「1Ωに流れる電流が2倍」より I_on = 2 I_off、すなわち E = 2 \times \frac{E}{1+R}。Eを消去すると 1+R = 2 で R=1\,\Omega。したがって正答は1Ωである。なお1Ωは電源と直列で常に回路電流と同一の電流が流れるため、この比較は妥当である。$
選択肢別解説
$R=0.2\,\Omega とすると電流比は \frac{I_{on}}{I_{off}} = 1+R = 1.2 で2倍にならないため不適。$
$R=0.5\,\Omega では電流比 1+R = 1.5。2倍の条件を満たさないため不適。$
$R=1\,\Omega では I_{off}=\frac{E}{1+1}=\frac{E}{2}、I_{on}=E となり I_{on}=2 I_{off} を満たす。よって正しい。$
$R=2\,\Omega では電流比 1+R = 3。2倍条件に合致しないため不適。$
$R=5\,\Omega では電流比 1+R = 6。2倍条件に合致しないため不適。$
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。