臨床工学技士問題表示
臨床工学技士国家試験
解説
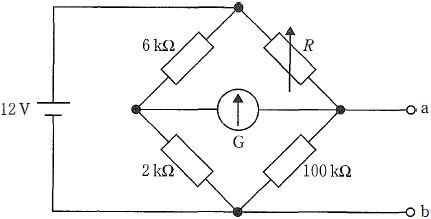
$検流計Gの振れがゼロはホイートストンブリッジの平衡を意味し、左右の分圧中点の電位が等しい(右側中点=端子aの電位V_aと、左側中点V_cが等しい)。このとき検流計には電流が流れないため、左右の枝は独立な単純な分圧回路として扱える。基準電位を端子b(電源の負極)とすると、左枝の6 kΩと2 kΩの直列分圧で中点電位は V_c=12 V \times (2 kΩ)/(6 kΩ+2 kΩ)=3 V。平衡より V_a=V_c=3 V であるから、求める ab 間電圧 V_ab=V_a-V_b=3 V。なお平衡条件から R/100 kΩ=6 kΩ/2 kΩ より R=300 kΩ となり、整合する。$
選択肢別解説
誤り。平衡時は左右中点の電位が等しく、左枝の分圧より中点電位は $12\,\text{V}\times\frac{2}{6+2}=3\,\text{V}$。したがって ab 間電圧は 3 V であり、1 V ではない。
誤り。検流計ゼロ→分圧中点が等電位。左枝の6 kΩと2 kΩの分圧から中点は $12\,\text{V}\times\frac{2}{8}=3\,\text{V}$。よって ab 間電圧は 3 V。
正しい。検流計の振れがゼロなら左右中点が等電位。基準を b=0 V とし、左枝の分圧で中点は $V=12\,\text{V}\times\frac{2}{6+2}=3\,\text{V}$。したがって $V_{ab}=3\,\text{V}$。
誤り。平衡条件のもとでは ab 間電圧は左枝の分圧で決まり $3\,\text{V}$。6 V にはならない。
誤り。平衡時の分圧より ab 間電圧は $3\,\text{V}$。9 V ではない。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
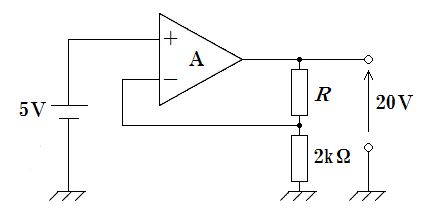
図は非反転増幅回路。理想演算増幅器では仮想短絡により反転入力(−)の電位は非反転入力(+)と等しくなり、V(−)=V(+)=5 V。反転端子は上側がR、下側が2 kΩで出力から接地へつながる帰還分圧回路なので、非反転増幅の式 $A_v=\frac{V_o}{V_i}=1+\frac{R}{2\,\text{k}\Omega}$ が成り立つ。図より $\frac{V_o}{V_i}=\frac{20}{5}=4$ だから、$4=1+\frac{R}{2\,\text{k}\Omega}\Rightarrow R=6\,\text{k}\Omega$。別解として、2 kΩには5 Vがかかるので電流は $I=\frac{5\,\text{V}}{2\,\text{k}\Omega}=2.5\,\text{mA}$。Rには $20-5=15$ Vがかかるため $R=\frac{15\,\text{V}}{2.5\,\text{mA}}=6\,\text{k}\Omega$。
選択肢別解説
R=2 kΩとすると非反転増幅の利得は $A_v=1+\frac{2}{2}=2$。入力5 Vに対して出力は10 Vとなり、図の20 Vと一致しないため誤り。
R=4 kΩなら $A_v=1+\frac{4}{2}=3$ で出力は15 V。20 Vに届かず不一致のため誤り。
R=6 kΩなら $A_v=1+\frac{6}{2}=4$。入力5 Vから出力は20 Vとなり図と一致。仮想短絡より反転端子も5 Vで、2 kΩに2.5 mA、Rには15 Vがかかるため $R=15/2.5\,\text{mA}=6\,\text{k}\Omega$。正しい。
R=8 kΩなら $A_v=1+\frac{8}{2}=5$ で出力は25 V。図の20 Vと合わず誤り。
R=10 kΩなら $A_v=1+\frac{10}{2}=6$ で出力は30 V。図の20 Vと合わず誤り。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
電池は起電力(開放電圧)Eと内部抵抗rが直列につながった等価回路で表せる。負荷抵抗Rを接続すると回路電流はオームの法則より $I = \frac{E}{r+R}$。これをRについて解くと $R = \frac{E}{I} - r$。与えられた値 E=9.0\,V、r=20\,\Omega、I=300\,mA=0.30\,A を代入すると $R = \frac{9.0}{0.30} - 20 = 30 - 20 = 10\,\Omega$。したがって負荷抵抗は10\,\Omega(選択肢3)が正しい。
選択肢別解説
誤り。R=2\,\Omega とすると電流は $I=\frac{E}{r+R}=\frac{9}{20+2}=\frac{9}{22}\approx0.409\,A$ となり、与えられた0.300\,Aと一致しない。
誤り。R=6\,\Omega では $I=\frac{9}{20+6}=\frac{9}{26}\approx0.346\,A$ で、0.300\,Aとは一致しない。
正しい。式 $R=\frac{E}{I}-r$ により $R=\frac{9.0}{0.30}-20=10\,\Omega$。検算でも $I=\frac{9}{20+10}=\frac{9}{30}=0.30\,A$ と一致する。
誤り。R=20\,\Omega では $I=\frac{9}{20+20}=\frac{9}{40}=0.225\,A$ となり、0.300\,Aと一致しない。
誤り。R=30\,\Omega では $I=\frac{9}{20+30}=\frac{9}{50}=0.18\,A$ で、0.300\,Aと一致しない。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
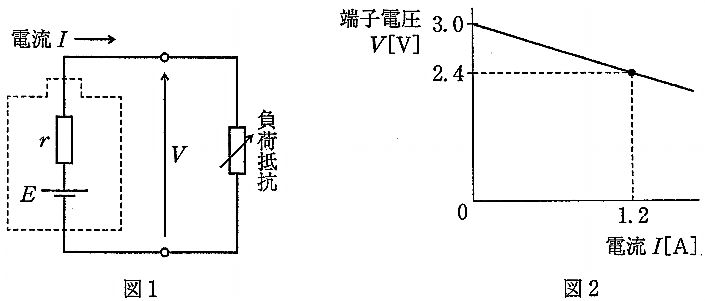
図2の直線は電池の等価回路(起電力Eと内部抵抗r)に対する関係式 $V=E-Ir$ を表す。グラフより開放時 ($I=0$) の端子電圧が $E=3.0\,\text{V}$、点 $(I,V)=(1.2\,\text{A},\,2.4\,\text{V})$ が与えられている。よって内部抵抗は $r=(E-V)/I=(3.0-2.4)/1.2=0.5\,\Omega$。短絡時は負荷抵抗が0で端子電圧 $V=0$ となり、電流は内部抵抗のみで制限されるため $I=E/r=3.0/0.5=6.0\,\text{A}$。したがって短絡電流は6 A。
選択肢別解説
短絡時は $I=E/r$ で与えられる。図2から $E=3.0\,\text{V}$、$r=0.5\,\Omega$ より $I=6\,\text{A}$ であり、0 Aではない。
図2の直線から $E=3.0\,\text{V}$、$r=0.5\,\Omega$ が得られるので、短絡電流は $I=E/r=6\,\text{A}$。1.5 Aは不一致。
短絡電流は $I=E/r=3.0/0.5=6\,\text{A}$。2 Aになる条件(例えば $r=1.5\,\Omega$ など)は図2と矛盾する。
3 Aであれば $I=E/r$ から $r=1.0\,\Omega$ となるが、図2の点 $(1.2,2.4)$ と開放電圧 $3.0\,\text{V}$ から求まる内部抵抗は $0.5\,\Omega$。よって誤り。
図2より $E=3.0\,\text{V}$、$r=(3.0-2.4)/1.2=0.5\,\Omega$。短絡時は $I=E/r=3.0/0.5=6\,\text{A}$ となるため正しい。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
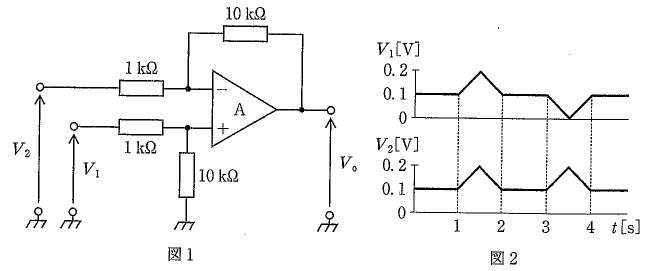
ただし、Aは理想演算増幅器とする。
解説
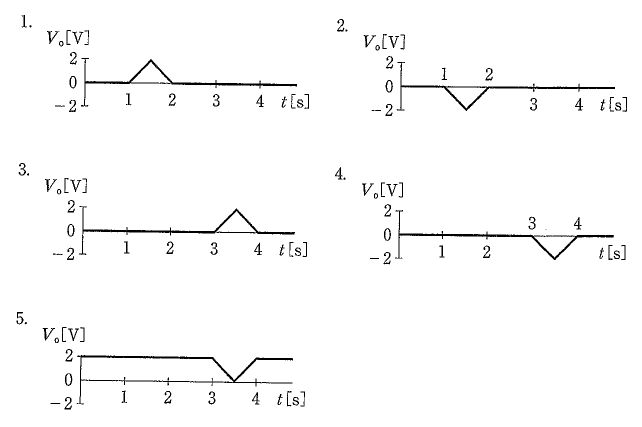
本回路は理想OPアンプを用いた差動増幅(減算)回路で、抵抗比が一致する(R1=R3、R2=R4)ときの一般式は $V_o=-\frac{R_2}{R_1}\,(V_1-V_2)$ となる。図の典型設定(例:R1=R3=1 k\Omega、R2=R4=10 k\Omega)では増幅率は $-10$。図2の入力波形から差電圧を読むと、0〜3 s と 5 s 以降は $V_1\approx V_2$ で $V_o\approx 0$、3〜4 s は $V_1-V_2=0.2-0.1=+0.1$ V より $V_o=-10\times 0.1=-1$ V、4〜5 s は $V_1-V_2=0.1-0.2=-0.1$ V より $V_o=-10\times(-0.1)=+1$ V となる。よって、3〜4 s で負、4〜5 s で正のピーク(絶対値1 V)となる波形が正しい。
選択肢別解説
不正解。3〜4 s で +1 V、4〜5 s で −1 V の符号入れ替えは、差動増幅の極性 $V_o=-\frac{R_2}{R_1}(V_1-V_2)$ と矛盾する。3〜4 s は $V_1-V_2=+0.1$ V なので $V_o=-1$ V、4〜5 s は $V_1-V_2=-0.1$ V なので $V_o=+1$ V となる。
不正解。3〜4 s で +1 V、4〜5 s で +2 V とするのは、符号も振幅も誤り。本回路の利得は約 −10、差電圧の絶対値は 0.1 V なので出力の絶対値は常に 1 V に一致する。
不正解。3〜4 s で −1 V は合うが、4〜5 s は $V_1-V_2=-0.1$ V より $V_o=+1$ V となるため、負のまま(−1 V)という記載は誤り。
正解。3〜4 s は $V_1-V_2=+0.1$ V で $V_o=-1$ V、4〜5 s は $V_1-V_2=-0.1$ V で $V_o=+1$ V。差動増幅の式 $V_o=-\frac{R_2}{R_1}(V_1-V_2)$ と整合し、絶対値は 1 V、極性は時間区間で反転する。
不正解。振幅を ±2 V とするのは過大。差電圧の絶対値 0.1 V に利得 10 を掛けるため、出力の絶対値は 1 V にとどまる。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
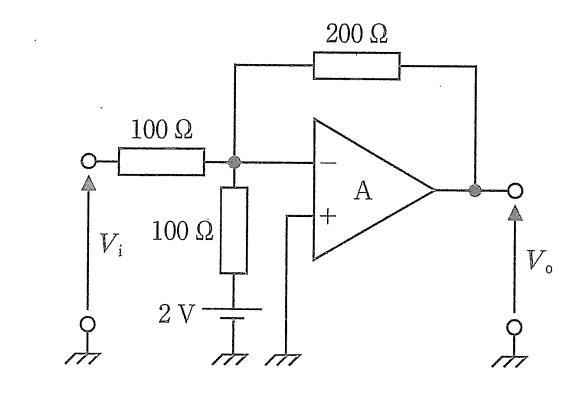
図の回路は、非反転入力(+)が接地された理想オペアンプの反転加算回路である。理想条件より仮想短絡が成り立ち、反転入力端子の電位は0 V、かつ入力端子電流は0とみなせる。反転端子ノードでKCLを立てると、$\frac{V_i-0}{100\,\Omega}+\frac{2\,\text{V}-0}{100\,\Omega}=\frac{0-V_o}{200\,\Omega}$。これを整理すると、$V_o=-200\,\Omega\left(\frac{V_i}{100\,\Omega}+\frac{2\,\text{V}}{100\,\Omega}\right)$。与えられた $V_i=5\,\text{V}$ を代入して、$V_o=-200\times(0.05+0.02)=-14\,\text{V}$。したがって正答は-14である。
選択肢別解説
正しい。反転加算回路として $V_o=-R_f\left(\frac{V_i}{R_1}+\frac{2\,\text{V}}{R_2}\right)=-200\left(\frac{5}{100}+\frac{2}{100}\right)=-14\,\text{V}$ となる。
誤り。$R_f=100\,\Omega$ と取り違えて反転ゲインを -1 と誤認し、$-1\times(5+2)=-7\,\text{V}$ とした可能性などの誤答。実際は $R_f=200\,\Omega$ である。
誤り。反転端子は仮想接地で0 Vだが、出力は入力電流の和で決まり、$V_i=5\,\text{V}$ と2 Vが加算されるため0 Vにはならない。0 Vになるのは例えば $V_i=-2\,\text{V}$ のように和が打ち消される場合で、本問の条件では該当しない。
誤り。符号反転を無視し、ゲインを -1 と誤って正のまま合計 $5+2=7\,\text{V}$ とした誤答。反転回路なので符号は負になる。
誤り。反転であることを無視して大きさのみ正の14 Vとした誤答。実際は -14 V である。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
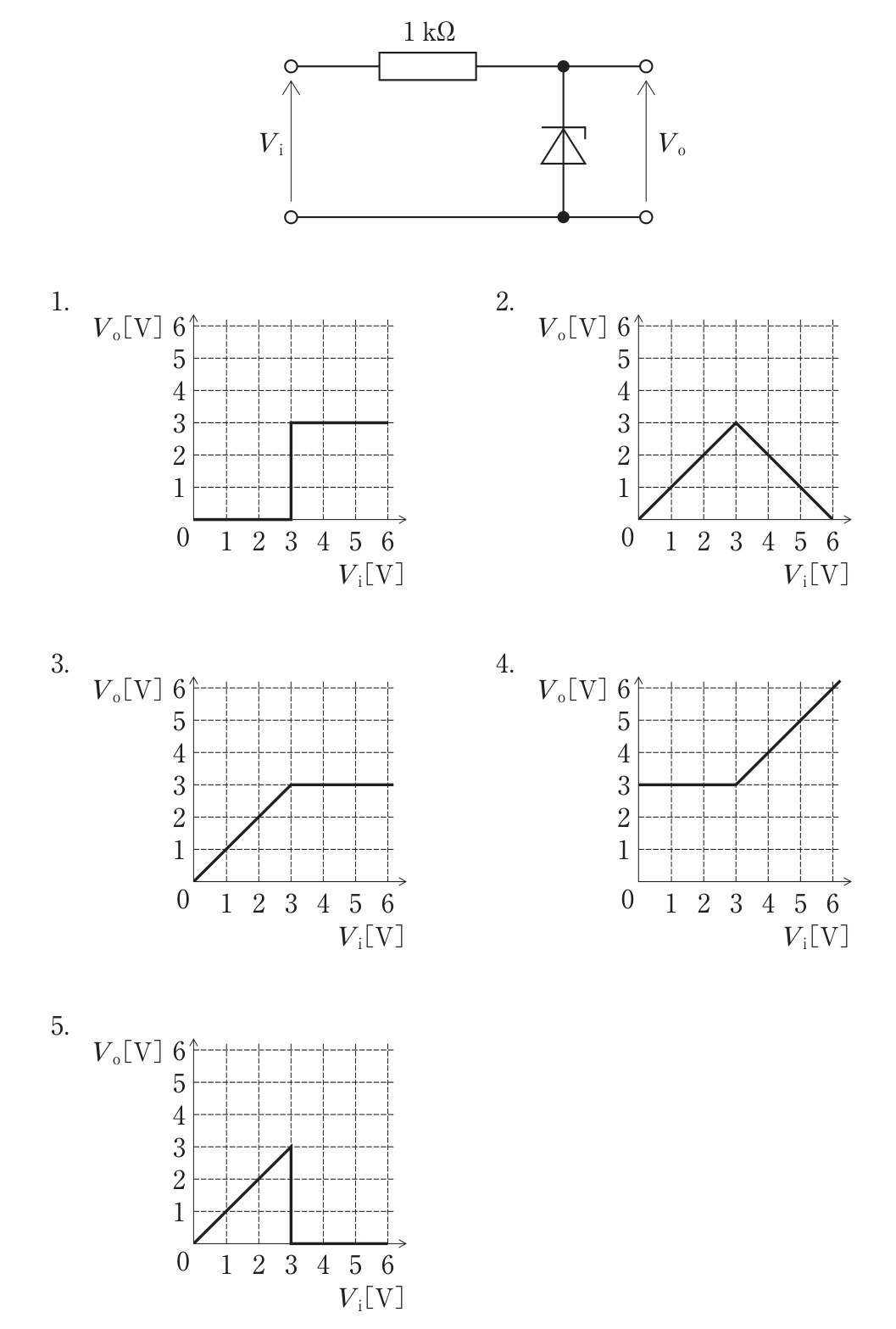
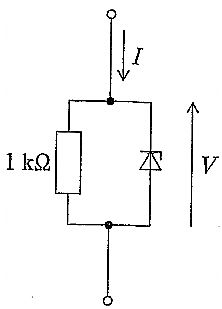
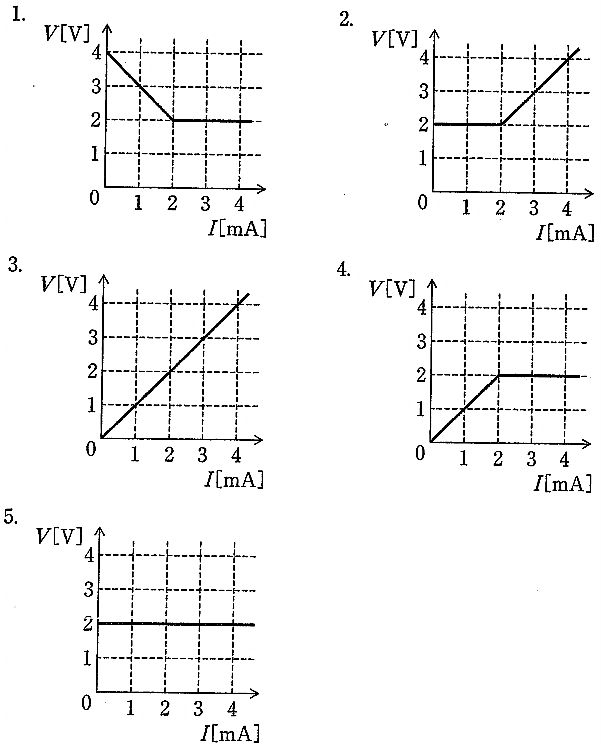
ツェナー電圧が2 Vのツェナーダイオードと1 kΩ抵抗の並列2端子回路のI–V特性は、端子電圧Vが2 V未満ではツェナーが非導通のため抵抗のみが電流を担い、オームの法則よりV=RIとなる。R=1 kΩなので、Iの単位をmAでとるとV(V)=I(mA)の直線で、I=2 mAでV=2 Vに到達する。Vが2 Vに達するとツェナーが降伏し、以後は電圧が約2 Vにクランプされるため、Iが増加してもVはほぼ一定(理想化)となる。したがって、電圧が直線的に増加した後、2 Vで飽和(一定)となる特性が正しい(選択肢4)。
選択肢別解説
電流増加で電圧が減少してから一定になる特性は負性抵抗的な挙動を含意し、本回路(抵抗とツェナーの並列)には該当しないため不適切。
電圧が一定になった後に再び増加する特性は、理想的なツェナーの定電圧動作と矛盾する。現実のツェナーには動的抵抗でわずかな上昇があるが、基礎問題では2 V付近で一定とみなすため不正解。
電流に比例して電圧が傾き1で増加し続けるのは純粋な1 kΩ抵抗のみの特性。ツェナーの降伏以降は電圧が約2 Vに保たれるため、本回路の全域特性としては誤り。
Iが小さい範囲(V<2 V)では抵抗支配でV=RI、I(mA)–V(V)表示ではV=Iの直線。I=2 mAでV=2 Vに達するとツェナーが降伏し、その後はV≃2 Vで一定となるため、この記述が正しい。
常に2 V一定であればIがどれだけ小さくてもV=2 Vとなるが、ツェナーは降伏前(V<2 V)ではほぼオフで抵抗のみが効くため、低電流域ではVは2 V未満。よって不適切。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
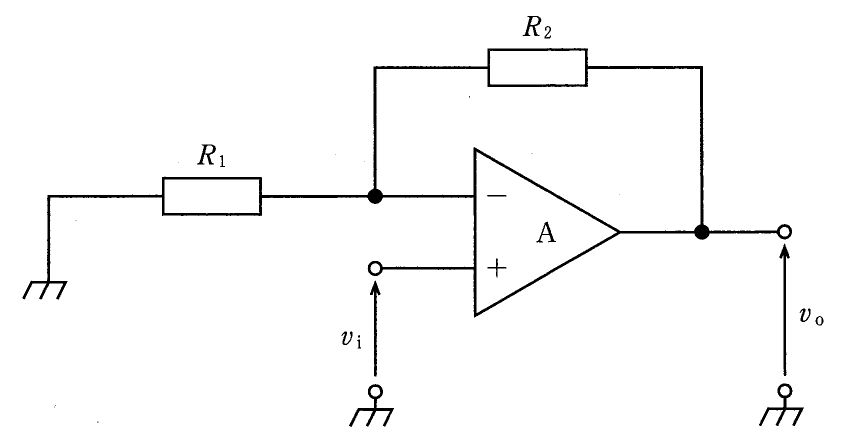
$図の回路は、非反転入力に信号 v_i を与え、反転入力側に R1(接地)と R2(帰還)を配した非反転増幅回路である。理想オペアンプの条件(入力端子電流は 0、負帰還動作中は仮想短絡により V_- = V_+ = v_i)より、反転端子ノード電位は v_i、よって R1 にかかる電圧は v_i、R1 を流れる電流は i_{R1} = v_i/R1 となる。また R2 を流れる電流は i_{R2} = (v_o - v_i)/R2 であり、反転入力へは電流が流れないため KCL から i_{R2} = i_{R1} が成り立つ。これより v_o = v_i\left(1 + \frac{R_2}{R_1}\right) で、増幅度は A_v = 1 + \frac{R_2}{R_1}。非反転入力側から見た入力抵抗は理想では無限大、理想オペアンプの出力抵抗は 0\,\Omega とみなす。これらに基づき、選択肢 3 \cdot 4 \cdot 5 が正しく、1 \cdot 2 は誤りである。$
選択肢別解説
$誤り。非反転増幅回路の電圧増幅度は A_v = 1 + \frac{R_2}{R_1} であり、符号も負にならない(負符号は反転増幅回路の特徴)。$
誤り。入力は非反転端子(+)で、理想オペアンプでは入力電流が 0 のため、入力抵抗は理想的に無限大であり R1 ではない。R1 は反転端子ノードと接地間の抵抗で、入力源からは直接見えない。
$正しい。理想オペアンプでは反転入力端子への電流が 0 のため、反転端子ノードの KCL より R2 を流れる電流 i_{R2} と R1 を流れる電流 i_{R1} は等しい。数式では i_{R1} = v_i/R1、i_{R2} = (v_o - v_i)/R2、かつ i_{R1} = i_{R2}。$
$正しい。負帰還下の理想オペアンプでは仮想短絡が成立し、反転端子電位 V_- は V_+ = v_i に等しい。R1 は V_- と接地の間にあるため、R1 に加わる電圧は v_i に等しい。$
$正しい。理想オペアンプの出力インピーダンスは 0\,\Omega と定義され、回路の出力抵抗も理想的に 0 とみなされる。$
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
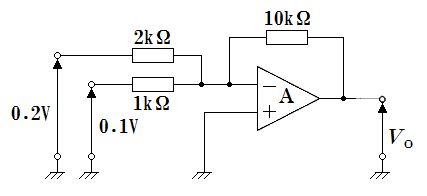
理想オペアンプの反転加算回路である。非反転入力は接地されているため、仮想短絡により反転入力端子の電位は 0 V とみなせる。よって反転入力ノードの電流収支より、$\dfrac{V_o-0}{R_f}= -\left(\dfrac{V_1-0}{R_1}+\dfrac{V_2-0}{R_2}\right)$、すなわち $V_o=-\left(\dfrac{R_f}{R_1}V_1+\dfrac{R_f}{R_2}V_2\right)$ となる。与えられた値 $R_1=2\,\text{k}\Omega$, $R_2=1\,\text{k}\Omega$, $R_f=10\,\text{k}\Omega$, $V_1=0.2\,\text{V}$, $V_2=0.1\,\text{V}$ を代入すると、$V_o=-(5\times 0.2+10\times 0.1)\,\text{V}=-(1.0+1.0)\,\text{V}=-2\,\text{V}$。したがって出力電圧は −2 V である。
選択肢別解説
不正解。計算により $V_o=-2\,\text{V}$ となるため、−1 V ではない。
正解。反転加算回路の式 $V_o=-\left(\dfrac{R_f}{R_1}V_1+\dfrac{R_f}{R_2}V_2\right)$ に値を代入すると $-2\,\text{V}$ となる。
不正解。本回路の電流収支から $V_o=-2\,\text{V}$ と求まるため、−3 V ではない。
不正解。理想オペアンプの仮想短絡を用いた計算結果は $V_o=-2\,\text{V}$。−4 V にはならない。
不正解。計算結果は $V_o=-2\,\text{V}$ であり、−5 V ではない。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
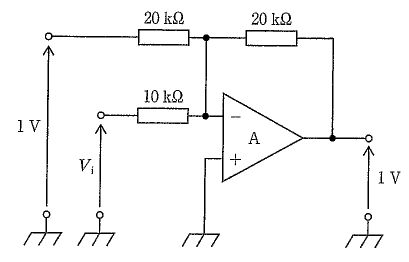
回路は理想オペアンプを用いた反転加算回路で、非反転端子(+)は接地されているため反転端子(−)の電位は仮想接地で約0 Vとなる。図より、反転端子に接続する抵抗は左の1 Vからの入力抵抗R1=20 kΩ、未知入力Viからの入力抵抗R2=10 kΩ、出力からの帰還抵抗Rf=20 kΩである。反転加算回路の関係は $V_o = - R_f ( V_1/R_1 + V_i/R_2 )$。図の値 $V_o=1\,\mathrm{V},\ V_1=1\,\mathrm{V},\ R_f=20\,\mathrm{k\Omega},\ R_1=20\,\mathrm{k\Omega},\ R_2=10\,\mathrm{k\Omega}$ を代入すると、$1 = -[1 + 2V_i]$ であり、$V_i=-1\,\mathrm{V}$ が得られる。
選択肢別解説
Vi=-2 V とすると $V_o = -20\,\mathrm{k\Omega}(1/20\,\mathrm{k\Omega} + (-2)/10\,\mathrm{k\Omega}) = -[1 - 0.2\times20] = 3\,\mathrm{V}$ となり、与えられた出力1 Vと一致しない。誤り。
反転加算回路の式 $V_o = - R_f ( V_1/R_1 + V_i/R_2 )$ に代入して $1 = -[1 + 2V_i]$ を解くと $V_i=-1\,\mathrm{V}$。正しい。
Vi=0 V なら $V_o = -20\,\mathrm{k\Omega}(1/20\,\mathrm{k\Omega} + 0)= -1\,\mathrm{V}$ となり、1 Vと一致しない。誤り。
Vi=1 V なら $V_o = -20\,\mathrm{k\Omega}(1/20\,\mathrm{k\Omega} + 1/10\,\mathrm{k\Omega}) = -3\,\mathrm{V}$。1 Vと一致しない。誤り。
Vi=2 V なら $V_o = -20\,\mathrm{k\Omega}(1/20\,\mathrm{k\Omega} + 2/10\,\mathrm{k\Omega}) = -5\,\mathrm{V}$。1 Vと一致しない。誤り。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
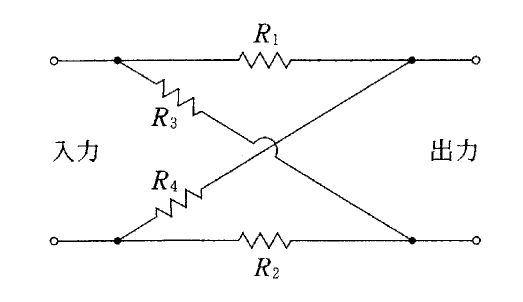
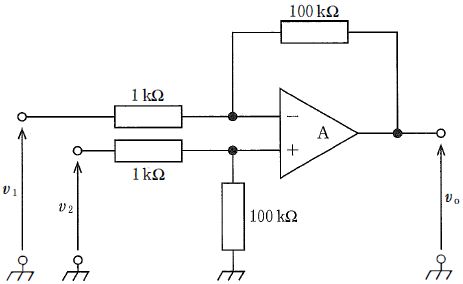
図の抵抗値は、反転側が V1→1 kΩ→(−)入力、(−)入力↔出力が100 kΩの帰還、非反転側が V2→1 kΩ→(+)入力、(+)入力→GNDが100 kΩで、比が $R_f/R_1=100$ かつ $R_4/R_3=100$ を満たすため、理想OPアンプの差動増幅回路として動作する。このとき出力は $v_o=\dfrac{R_f}{R_1}(v_2-v_1)$。値を代入すると $v_o=100\times(10\,\text{mV}-20\,\text{mV})=100\times(-10\,\text{mV})=-1\,\text{V}$。$v_1>v_2$ なので出力の極性は負になる。
選択肢別解説
誤り。差動利得は100、差電圧は $v_2-v_1=-10\,\text{mV}$ なので $v_o=-1\,\text{V}$。−10 V は桁違い。
正しい。差動増幅回路で $v_o=\dfrac{R_f}{R_1}(v_2-v_1)=100\times(-10\,\text{mV})=-1\,\text{V}$ となる。
誤り。$v_2-v_1$ が負であるため出力は負極性となり、+1 V にはならない。
誤り。利得と単位換算を正しく適用すると −1 V。+10 V は極性も大きさも不適切。
誤り。利得100を差電圧 −10 mV に掛けると −1 V。100 V にはならない。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
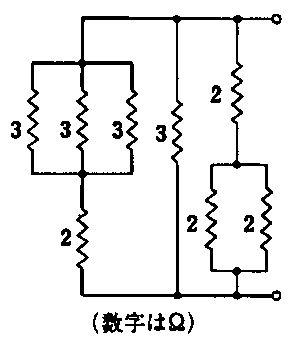
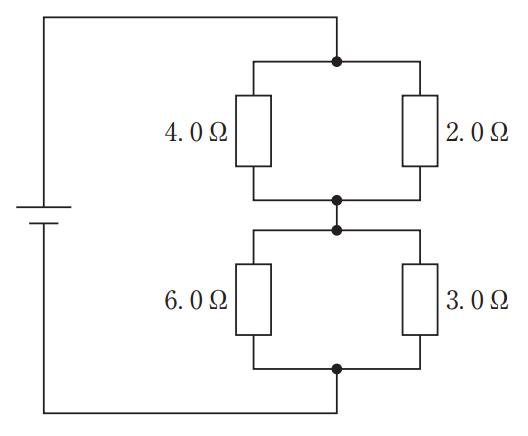
抵抗2.0\Omegaの消費電力が2.0 Wと与えられているので、その両端電圧は$V=\sqrt{PR}=\sqrt{2.0\times2.0}=2.0\ \text{V}$となる。図より2.0\Omegaと4.0\Omegaは並列接続であり、並列要素の両端電圧は等しいため、4.0\Omegaにも同じ2.0 Vがかかる。よって4.0\Omegaの消費電力は$P=V^2/R=2.0^2/4.0=1.0\ \text{W}$である。下段の並列群(6.0\Omegaと3.0\Omega)は上段と直列だが、本問は上段並列内の電圧から直接求まるため影響しない。
選択肢別解説
誤り。4.0\Omegaに流れる電流は$I=V/R=2.0/4.0=0.5\ \text{A}$であるが、問われているのは消費電力。電力は$P=I^2R=(0.5)^2\times4.0=1.0\ \text{W}$。
正しい。2.0\Omegaの2.0 Wから上段並列の端子電圧は$V=2.0\ \text{V}$と求まる。4.0\Omegaの電力は$P=V^2/R=2.0^2/4.0=1.0\ \text{W}$。
誤り。上段並列の端子電圧は2.0 Vであり、4.0\Omegaの電力は$P=2.0^2/4.0=1.0\ \text{W}$となるため1.5 Wにはならない。
$誤り。2.0 Wは与えられた2.0\Omega抵抗の消費電力であり、4.0\Omegaの電力は1.0 W。$
$誤り。計算上、4.0\Omegaの消費電力は1.0 Wであり3.0 Wにはならない。$
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。