臨床工学技士問題表示
臨床工学技士国家試験
検索元問題
第30回 午前 第56問
20件の類似問題
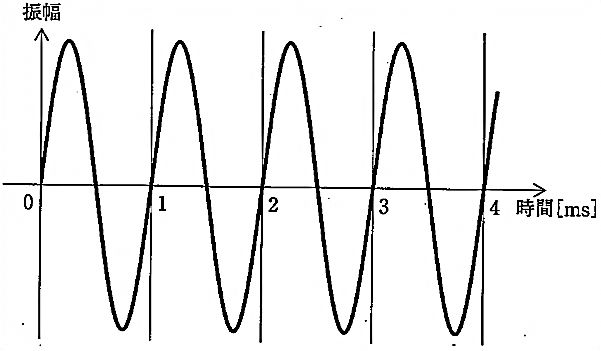
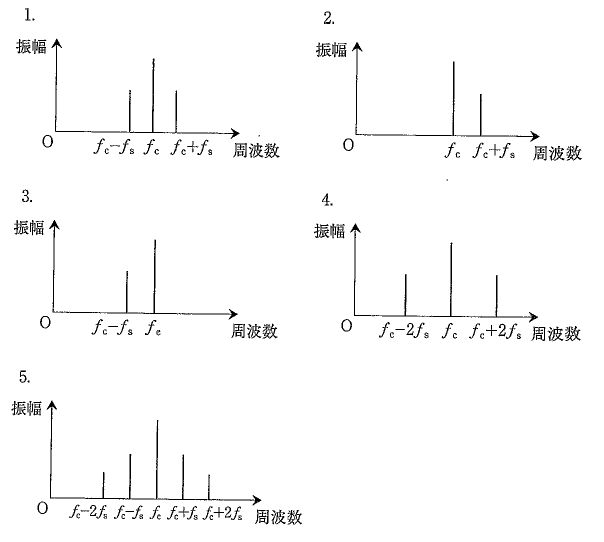
図の変調方式はどれか。...
広告
55
臨床工学技士国家試験 -
第25回 午前
正答率:51%
類似度 55.6%
振幅変調(AM)において変調波が1~2kHzの周波数帯域を持つ信号で搬送波の周波数が1,000kHzであるとき、被変調波の側波について正しいのはどれか。
a
上側波帯の最高周波数は1,002kHzである。
b
上側波帯の最低周波数は1,000kHzである。
c
下側波帯の最高周波数は998kHzである。
d
下側波帯の帯域幅は 2 kHz である。
e
上・下側波帯の周波数スペクトルは対称である。
組み合わせ:
1. a b
2. a e
3. b c
4. c d
5. d e
広告
57
臨床工学技士国家試験 -
第28回 午前
重要度:低
正答率:64%
類似度 54.6%
正しい組合せはどれか。
a
ASK -------------- 振幅偏移変調
b
PSK -------------- パルス偏移変調
c
TDM -------------- 波長分割多重
d
CDMA ------------- パルス符号変調
e
FDM -------------- 周波数分割多重
組み合わせ:
1. a b
2. a e
3. b c
4. c d
5. d e
31
臨床工学技士国家試験 -
第11回 午後
類似度 54.5%
通信において正しいのはどれか。
a
受信波から信号を取り出す操作を復調という。
b
PCMでは信号を符号化して伝送する。
c
FMはAMより狭い周波数帯域を用いる。
d
電話回線を使えば心電図を変調せずそのまま伝送することができる。
e
ディジタル多重化伝送には時分割方式より周波数分割方式が適している。
組み合わせ:
1. a b
2. a e
3. b c
4. c d
5. d e
広告
広告
56
臨床工学技士国家試験 -
第29回 午後
重要度:最重要
正答率:66%
類似度 53.9%
振幅変調において信号v(t)= 3 sin(2000πt)で1000 kHzの搬送波を変調するとき、被変調波の上下側波の周波数[kHz]はどれか。ただし、時間tの単位は秒とし、過変調は生じないものとする。
1
980 と1020
2
990 と1010
3
997 と1003
4
998 と1002
5
999 と1001
5
臨床工学技士国家試験 -
第1回 午後
類似度 53.7%
信号処理について正しいのはどれか。
a
心電図をA/D変換するには、0.1Hzのサンプリング(標本化)周波数で十分である。
b
不規則雑音に埋もれた繰り返し信号を検出するには加算平均法が有効である。
c
計算機内のデータをペンレコーダに描かせるにはD/A変換が必要である。
d
A/D変換を行うと一般に信号対雑音比(S/N)が向上する。
e
高速フーリエ変換(FFT)を行うと信号対雑音比が向上する。
組み合わせ:
1. a b
2. a e
3. b c
4. c d
5. d e
35
臨床工学技士国家試験 -
第21回 午後
正答率:82%
類似度 53.4%
図のシステム伝達関数はどれか。
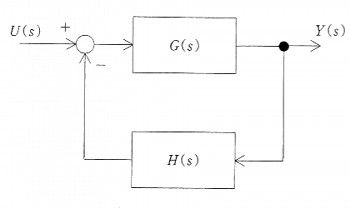
1
$\frac {1}{G\left( s\right) H\left( s\right) }$
2
$\frac {G\left( s\right) }{1-G\left( s\right) H\left( s\right) }$
3
$\frac {G\left( s\right) }{1+G\left( s\right) H\left( s\right) }$
4
$\frac {G\left( s\right) H\left( s\right) }{1-G\left( s\right) H\left( s\right) }$
5
$\frac {G\left( s\right) H\left( s\right) }{1+G\left( s\right) H\left( s\right) }$
広告