医用機械工学の過去問
国試第37回午前:第86問
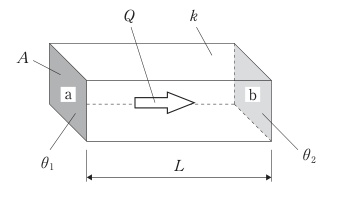
ハーゲン・ポアズイユの式はどれか。ただし、Qを流量、ΔPを圧力差、rを管の半径、ηを粘性率、Lを管の長さとする。
1:$Q = \frac{\Delta P \cdot \mu \pi r^4}{8L}$
2:$Q = \frac{\Delta P \cdot \mu \pi r^2}{8L}$
3:$Q = \frac{\Delta P \cdot r^2}{8\mu \pi L}$
4:$Q = \frac{\Delta P \cdot \pi r^4}{8\mu L}$
5:$Q = \frac{\Delta P \cdot \pi r^2}{8\mu L}$