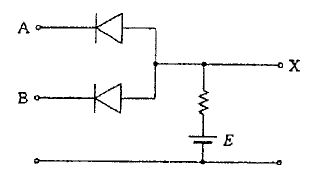
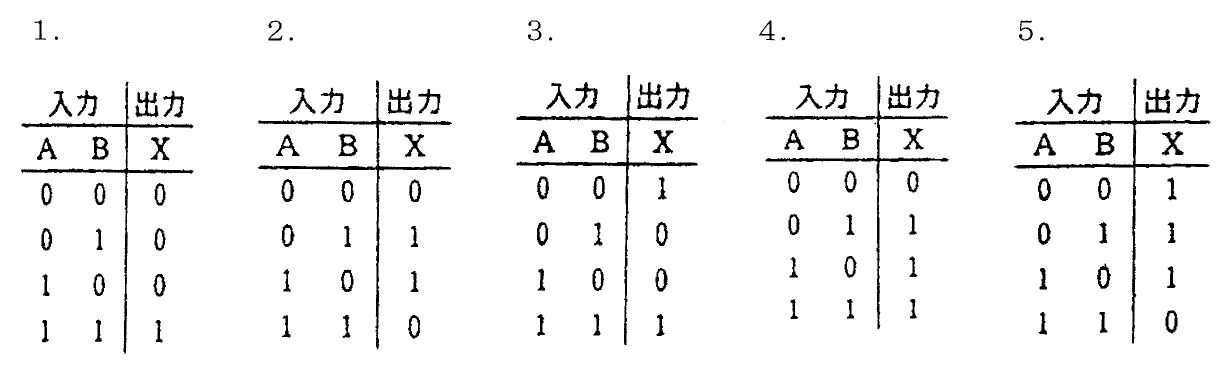
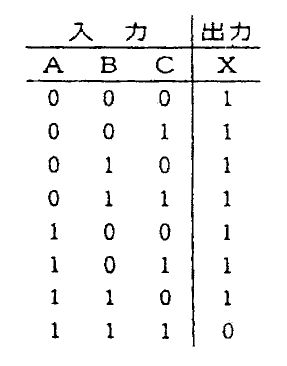
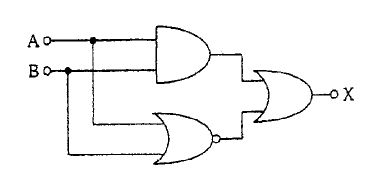
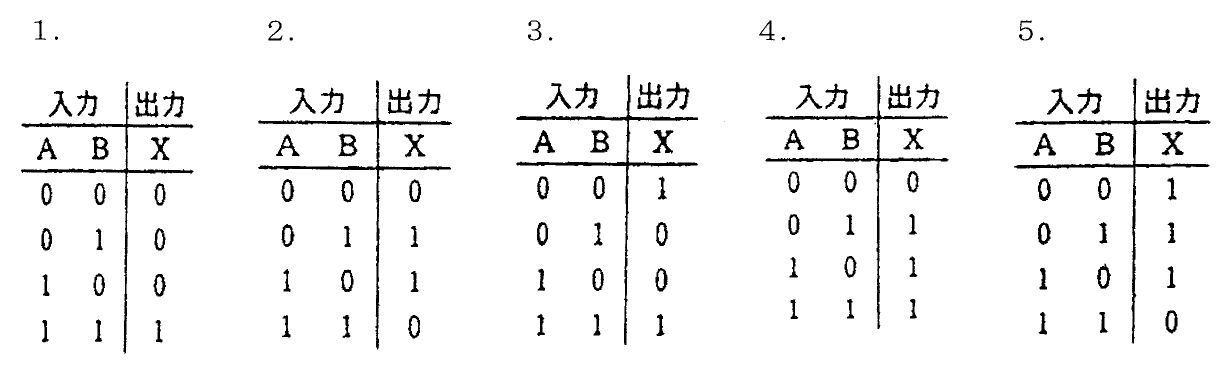
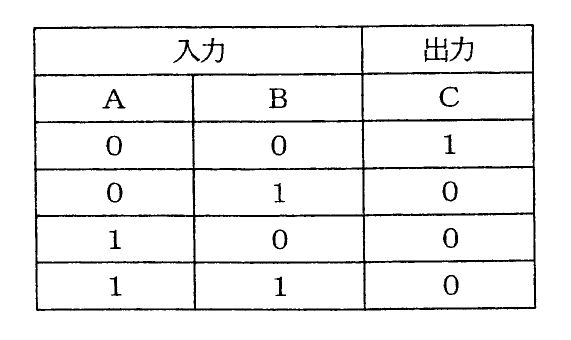
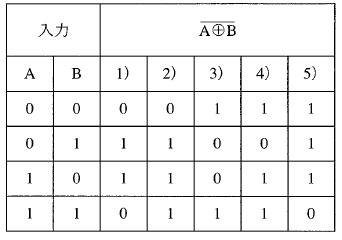
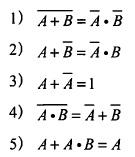臨床工学技士問題表示
臨床工学技士国家試験
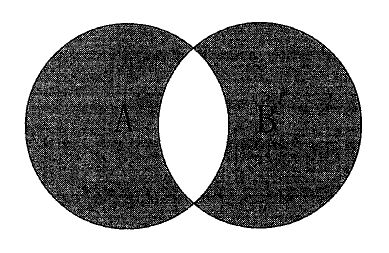
解説
図の網掛けは、AとBのうち重なり部分を除外した左右の部分のみを示している。これは集合の対称差であり、論理演算では排他的論理和(Exclusive OR, XOR)に相当する。集合式で表すと $A \oplus B = (A \cap \bar{B}) \cup (\bar{A} \cap B)$。ANDは共通部分 $A \cap B$、ORは和集合 $A \cup B$、NOTは単項の補集合、NORは $\overline{A \cup B}$(2つの円の外側)であり、いずれも図の網掛けには一致しない。
選択肢別解説
AND(論理積)は集合では $A \cap B$(重なり部分のみ)。図は重なりを除外しているため一致しない。
OR(論理和)は集合では $A \cup B$(2つの円全体、重なりも含む)。図は重なりを含まず左右のみなので一致しない。
NOT(否定)は単一集合に対する補集合(例: $\bar{A}$)であり、2集合の対称差ではない。図の網掛けとは一致しない。
Exclusive OR(排他的論理和, XOR)は $A \oplus B = (A \cap \bar{B}) \cup (\bar{A} \cap B)$。図はまさに重なりを除いたA側とB側の部分であり、XORに一致する。
NOR(否定論理和)は $\overline{A \cup B}$ で2つの円の外側全域を示す。図は円の内側の対称差であり一致しない。
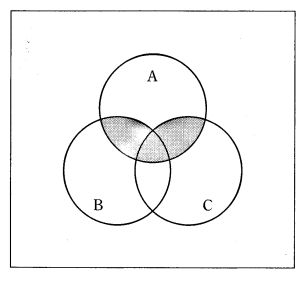
解説
網掛けは「A と C の共通部分から、B に属する部分を除いた領域」を示す。集合論とブール代数の対応は、共通部分が論理積($\cdot$)、和集合が論理和(+)、補集合が否定(上線 $\overline{\ }$)である。よって条件は「A かつ C かつ 非B」となり、論理式は $A\cdot \overline{B}\cdot C$ が適合する。
選択肢別解説
正しい。A と C の共通部分($A\cdot C$)のうち、B でない部分($\overline{B}$)を取るので $A\cdot \overline{B}\cdot C$ が網掛け領域を正確に表す。中央の三つ共通部分($A\cdot B\cdot C$)は $\overline{B}$ により除外される。
誤り。$A\cdot B\cdot C$ は A・B・C の三つ全てに共通する中央の小領域のみを指す。網掛けは B を除いた A∩C 部分であり、中央の三重共通領域は含まれない。
誤り。$A+\overline{B}\cdot C$ は「A 全体」または「B でなく C」の和であり、A 単独の領域や C で B に属さない領域まで含むため、網掛けより広すぎる。
誤り。$A\cdot B + C$ は「A∩B」または「C 全体」であるため、C の全域を含み過大。網掛けは A∩C から B 部分を除いた狭い領域である。
誤り。$\overline{(A+B)}\cdot C$ はド・モルガンの法則より $(\overline{A}\cdot \overline{B})\cdot C$、すなわち「C に属し、かつ A にも B にも属さない部分」を意味する。網掛けは A に属しているため一致しない。
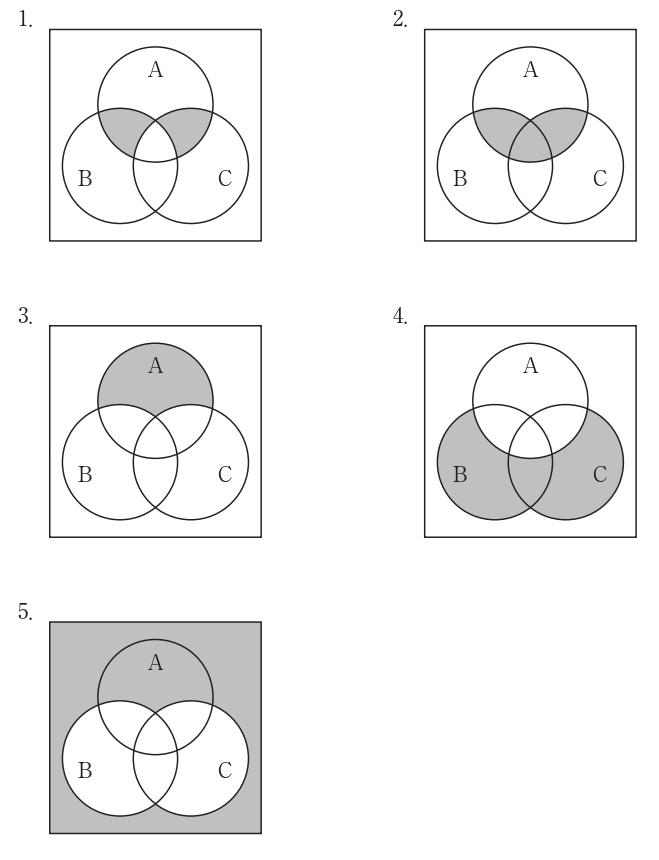
解説
提示された数式表記 "$A_{B}\left( \overline{B+C}\right)$" は論理演算として不自然で、少なくとも "A" と括弧内の積(AND)を示す中点 $\cdot$ の脱落、あるいは式そのものの誤記が疑われる。実際の図を確認すると、選択肢3は集合A全体が網掛けされており、これは論理式 $A$ に対応する。与えられた正答フラグ(3が正答)および図の内容に基づけば、求められている領域はA全体と解釈でき、よって図3が適合する。なお、もし式が $A\cdot\overline{B+C}=A\cdot\overline{B}\cdot\overline{C}$ を意図していたなら、AのうちBにもCにも属さない部分のみが網掛けされるはずで、今回の選択肢3(A全域)とは一致しない。
選択肢別解説
図1はAとBの共通部分およびAとCの共通部分(中心の三重共通部を含む領域)に相当し、これは $A\cap(B\cup C)$ を表す。A全体ではないため不適。
図2はAの一部(他集合との重なり部分)だけが網掛けであり、A全域や $A\cdot\overline{B+C}$ を表すものではないため不適。
図3は集合Aの領域全体が網掛けであり、論理式 $A$ を表す。問題の数式表記には不自然さがあるが、与えられた正答フラグおよび図の内容から本図が要求領域に一致する。
図4は主として集合Bおよび集合C側が網掛けされており(中心の重なりの扱いはあるが)、A全体や $A\cdot\overline{B+C}$ には該当しないため不適。
図5はA・B・Cのいずれにも属さない外部領域($\overline{A\cup B\cup C}$)が網掛けであり、Aや $A\cdot\overline{B+C}$ ではないため不適。
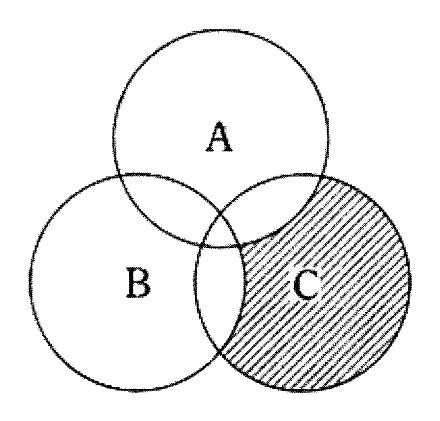
解説
論理積「・」は共通部分(AND, ∩)、論理和「+」は和集合(OR, ∪)を表す。図の網かけは A と B の共通部分および A と C の共通部分(中央の A∩B∩C も含む)であり、これは (A∩B)∪(A∩C) に等しい。分配法則より (A∩B)∪(A∩C) = A∩(B∪C) となるので、論理式は A・(B + C) が適合する。
選択肢別解説
A・(B + C) は A∩(B∪C) を意味し、分配して (A∩B)∪(A∩C) に等しい。図の網かけ(A∩B と A∩C、およびその重複である A∩B∩C を含む)と一致する。
B・(A + C) は B∩(A∪C) = (A∩B)∪(B∩C)。B∩C のみ(A に含まれない部分)も含むため、図の網かけにはない領域が余分に入ってしまい一致しない。
A + B・C は A∪(B∩C) を表す。A 全域が含まれるため、図の網かけ(A のうち B または C と重なる部分のみ)より広く一致しない。
B + A・C は B∪(A∩C) を表す。B 全域を含み、図の網かけより広く一致しない。
C + A・B は C∪(A∩B) を表す。C 全域を含み、図の網かけより広く一致しない。
解説
与式は意図として $(A+B)\cdot \overline{C}$(A または B かつ C でない)と読むのが妥当であり、ベン図では A と B の和集合のうち C の円に含まれない部分を網かけする。すなわち $(A\cup B)\cap \overline{C}$ に相当し、A のみ・B のみ・A\cap B のうち C 外側が対象となる。添付図では選択肢1の網かけがこれに一致する。なお原文にある「-\overline{C}」は集合差と解される記号で、そのまま厳密に解釈すると $(A+B)-\overline{C}=(A\cup B)\cap C$ となり本図の正答と整合しないため、記号の誤記(本来は積“\cdot”)と判断した。
選択肢別解説
正しい。A と B の和集合から C の領域を除いた部分が網かけされており、$(A+B)\cdot \overline{C}=(A\cup B)\cap \overline{C}$ を表している。
不正解。図では B と C の共通部分のみが網かけに見え、$B\cdot C$ を示す。$(A+B)\cdot \overline{C}$(A または B かつ C でない)とは一致しない。
不正解。図の網かけは A と B の共通部分のみ(少なくとも A や B の単独領域は含まれていない)で、$A\cdot B$ を表す。$(A+B)\cdot \overline{C}$ では A や B の単独領域(C 以外)が含まれるため不一致。
不正解。A と B の和集合全体が網かけされており、$A+B$($A\cup B$)を示す。C を除外する条件 $\overline{C}$ が反映されていない。
不正解。A と C の共通部分が網かけで、$A\cdot C$ を表す。$(A+B)\cdot \overline{C}$ とは異なる。
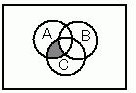
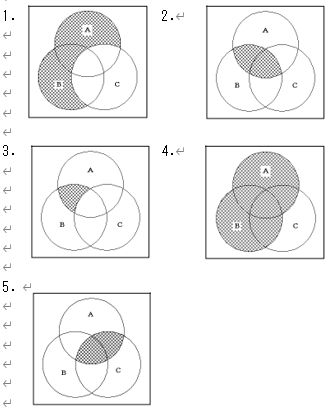
解説
論理式 F = A・B + B・C + C・A は、3つの集合(または論理変数)A, B, C のうち少なくとも2つが真となる領域を表す。ベン図では、A∩B、B∩C、C∩A の3つの共通部分の和集合を塗ることになる。なお中央の三重共通部分 A∩B∩C は、たとえば A∩B に完全に含まれるため(吸収則:A・B + A・B・C = A・B)、必ず含まれる。従って、三つの円の相互の重なり(2つ以上が重なる部分)をすべて含む図が正しい。
選択肢別解説
中央の三重共通部分のみが塗られている図で、これは A・B・C を表す。F は A・B、B・C、C・A の和であり、三重共通部分だけに限定しないため不適切。
各ペアの共通部分が塗られているが、中央の三重共通部分が除外されている図に相当する。F では A・B、B・C、C・A のいずれにも A・B・C が含まれるため、中央も含めて塗る必要がある。よって不正解。
A∩B、B∩C、C∩A の全てを含み、中央の三重共通部分も含む領域が塗られている。これは F = A・B + B・C + C・A(少なくとも2つが真)のベン図表現に一致するため正しい。
3つの円全体(A ∪ B ∪ C)が塗られている図で、これは A + B + C を表す。単独の集合のみが真の領域まで含むため F より広く、不適切。
A ∪ B ∪ C から中央の三重共通部分 A・B・C を除いた領域が塗られている図に相当する。これは (A + B + C) − (A・B・C) を表し、F とは一致しない。