臨床工学技士問題表示
臨床工学技士国家試験
解説
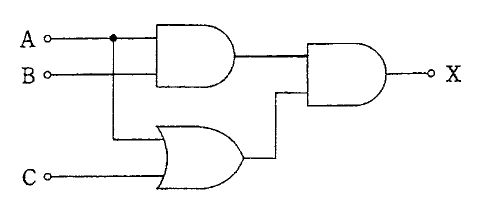
$図の回路は、上段のANDゲートで D = A\cdot B、下段のORゲートで E = A + C を生成し、最後にANDで結合して X = D\cdot E = A\cdot B\cdot (A + C) となる。ブール代数の吸収律 A\cdot (A + C) = A を用いると、X = A\cdot B に簡約できる。よって出力Xを表す論理式は A \cdot B(= A\cdot B)である。$
選択肢別解説
$正しい。回路の合成式は X = A\cdot B\cdot (A + C)。吸収律 A\cdot (A + C) = A により X = A\cdot B となる。$
$誤り。提案式は X = A\cdot B + C。例えば A=0, B=0, C=1 のとき、A\cdot B + C = 1 だが、回路は X = (0)\cdot(0+1)=0 で一致しない。$
$誤り。提案式は X = A + B\cdot C。例えば A=0, B=1, C=1 のとき、A + B\cdot C = 1 だが、回路は D=0, E=1, X=0 で一致しない。$
誤り。A + B + C は3入力OR。実際の回路は最初に A と B のANDを要求するため、A=0, B=1, C=0 などで OR は1でも回路の出力は0となる。
$誤り。A\cdot B\cdot C は3入力AND。例えば A=1, B=1, C=0 でこの式は0だが、回路は X = 1\cdot(1+0)=1 となり一致しない。$
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
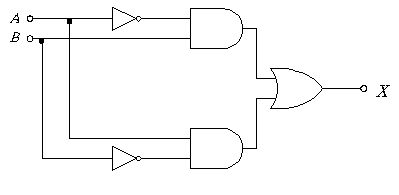
図は、入力AとBから2系統のANDを作り、その2出力をORで合成する構成である。上段はAがNOTを通ってからBとANDされるため $\overline{A}\cdot B$、下段はBがNOTを通ってAとANDされるため $A\cdot \overline{B}$ となる。最終的にORで和をとるので、出力は $X=\overline{A}\cdot B+A\cdot \overline{B}$。これは排他的論理和(XOR)の標準形であり、AとBが異なるときのみ1になる。
選択肢別解説
$\overline{A}\cdot\overline{B}+A\cdot B$ はAとBが同じとき1になる式で、排他的論理和の否定(XNOR)である。図の回路(XOR)とは一致しないため不正解。
$\overline{A}\cdot B+A\cdot \overline{B}$ はXORの標準形。図では上段が $\overline{A}\cdot B$、下段が $A\cdot \overline{B}$ を生成し、ORで合成しているためこの式が出力Xに対応する。正解。
$(A+B)\cdot(A+\overline{B})$ は分配・吸収を用いて $A+B\cdot\overline{B}=A+0=A$ に簡約される。XORではなくAに等しいため不正解。
提示テキストでは選択肢3と同一の $(A+B)\cdot(A+\overline{B})$ となっており、同様に $A$ に簡約されるため不正解。重複表記の可能性がある(詳細はtypo_check参照)。
$\overline{A}\cdot(A+B)+B\cdot(\overline{A}\cdot\overline{B})=\overline{A}A+\overline{A}B+B\overline{A}\overline{B}=0+\overline{A}B+0=\overline{A}B$ に簡約される。XORの一部項のみであり、図の出力とは一致しないため不正解。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
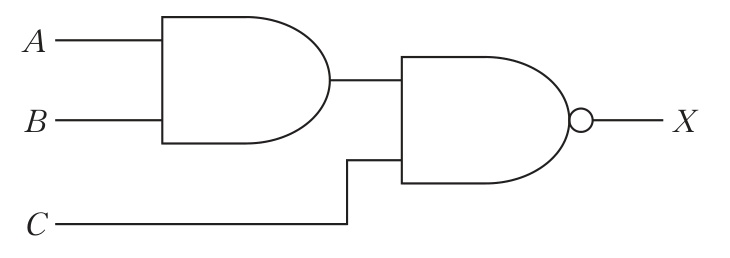
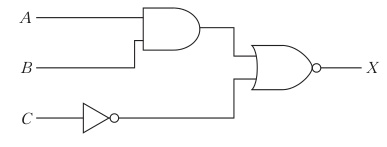
図の回路は、A と B をANDに入力し D = A \cdot B、C をインバータで反転して E = \overline{C} を得る。これら D と E がNORゲートに入るので、出力は X = \overline{D + E} = \overline{(A \cdot B) + \overline{C}} となる。ド・モルガンの定理 $\overline{P+Q}=\overline{P}\cdot\overline{Q}$ を用いると X = \overline{(A \cdot B)} \cdot C。さらに $\overline{P\cdot Q}=\overline{P}+\overline{Q}$ を用いて X = (\overline{A}+\overline{B}) \cdot C に一致する。よって等価な論理式は選択肢3である。
選択肢別解説
$X = A \cdot B + C$ はANDの結果と C のOR。実回路の出力は $X = \overline{(A \cdot B) + \overline{C}}$ であり一致しない。例えば A=1, B=1, C=1 で、本式は 1、回路は $\overline{1+0}=0$ となり不一致。
$X = A \cdot B + \overline{C}$ は OR 出力で否定がないため、NOR 出力である回路と一致しない。例えば A=0, B=0, C=0 で本式は $0+1=1$、回路は $\overline{0+1}=0$。
$X = (\overline{A} + \overline{B}) \cdot C$。回路式 $X = \overline{(A \cdot B) + \overline{C}}$ にド・モルガンの定理を2回適用すると $(\overline{A}+\overline{B})\cdot C$ となり等価。
$X = (A + B) \cdot C$ は OR の後に C とのAND。回路の NOR 出力とは一般に一致しない。例えば A=0, B=0, C=1 で本式は $0\cdot1=0$、回路は $\overline{0+0}=1$。
$X = (A + B) \cdot \overline{C}$ は OR の後に $\overline{C}$ とのAND。回路の式とは異なる。例えば A=0, B=0, C=1 で本式は $0\cdot0=0$、回路は $\overline{0+0}=1$ で不一致。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
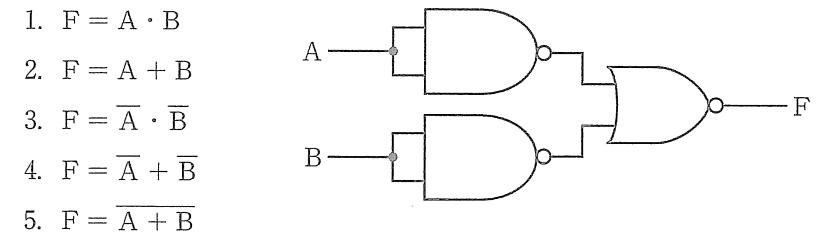
$図の回路は,入力A \cdot Bがそれぞれ2入力NANDゲートの両入力を短絡して与えられており,これらはインバータとして働くため,上段出力はX=\overline{A},下段出力はY=\overline{B}となる。最終段はORゲートの出力に否定バブルが付いたNORゲートで,F=\overline{X+Y}=\overline{\overline{A}+\overline{B}}。ド \cdot モルガンの定理より F=\overline{\overline{A}}\cdot\overline{\overline{B}}=A\cdot B。したがって正しい論理式はAとBの論理積である。$
選択肢別解説
$正しい。回路全体は F=\overline{\overline{A}+\overline{B}} と表せ,ド \cdot モルガンの定理で F=A\cdot B に等しい。$
誤り。これはORゲートの式 F=A+B。図の最終段はNORであり,前段がインバータのため全体はANDに等しく,ORにはならない。
$誤り。F=\overline{A}\cdot\overline{B} はド \cdot モルガンの定理より \overline{A+B}(NOR)に等しい。図の回路はNORの前に反転が入っており,最終的にANDとなる。$
$誤り。F=\overline{A}+\overline{B} は \overline{A\cdot B}(NAND)に等しい。図の回路の等価はANDであり一致しない。$
$誤り。F=\overline{A+B} はNORの式。図ではAとBを一度反転してからNORをとるため,全体はANDとなる。$
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
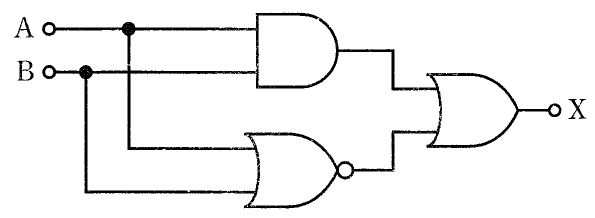
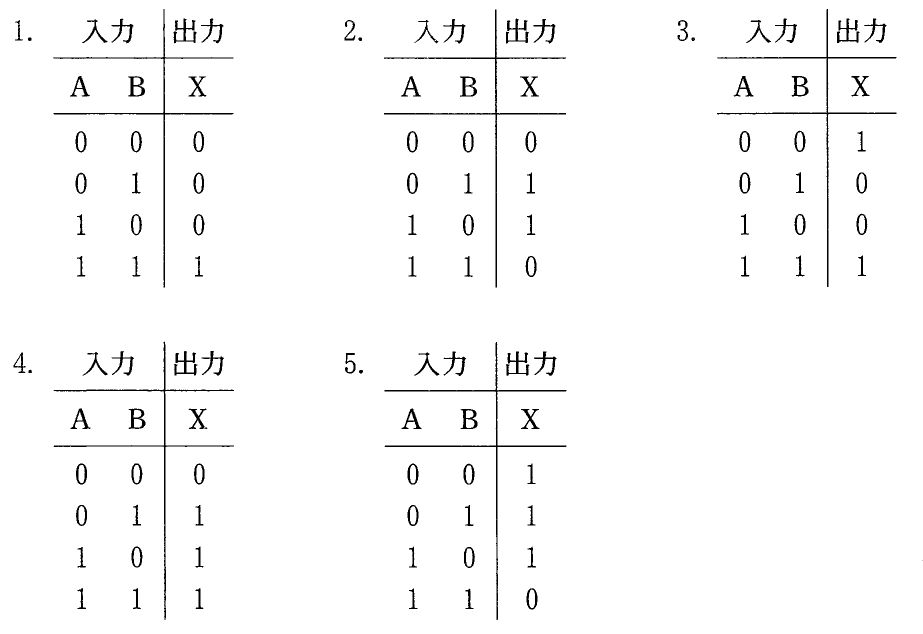
$提示された回路は、入力A \cdot Bから中間で A\cdot\bar{B} と \bar{A}\cdot B を生成し、それらをORで合成して X = A\cdot\bar{B} + \bar{A}\cdot B となる構成(排他的論理和, XOR)として解釈できる。XORはAとBが異なるときのみ1となるため、真理値表は (A,B)=(0,0)→0, (0,1)→1, (1,0)→1, (1,1)→0 である。したがって該当する真理値表が正答。$
選択肢別解説
$誤り。これはANDの真理値表で (1,1) のときのみ1となる(X = A\cdot B)。本回路の出力は X = A\cdot\bar{B} + \bar{A}\cdot B(XOR)であり、(0,1) と (1,0) でも1になるため一致しない。$
誤り。これはORの真理値表(X = A + B)で、(1,1) でも1となる。XOR は (1,1) で0となるため一致しない。
$正しい。XORの真理値表であり、X = A\cdot\bar{B} + \bar{A}\cdot B に対応する。各入力組み合わせで (0,0)→0, (0,1)→1, (1,0)→1, (1,1)→0 となり、本回路の動作と一致する。$
$誤り。これはXNOR(排他的論理和の否定)で、入力が等しいとき1、異なるとき0(X = A\cdot B + \bar{A}\cdot\bar{B})。XORとは出力がちょうど逆になる。$
$誤り。これはNANDの真理値表(X = \overline{A\cdot B} = \bar{A} + \bar{B})で、(0,0) を含む3パターンで1となる。XORは (0,0) で0となるため一致しない。$
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
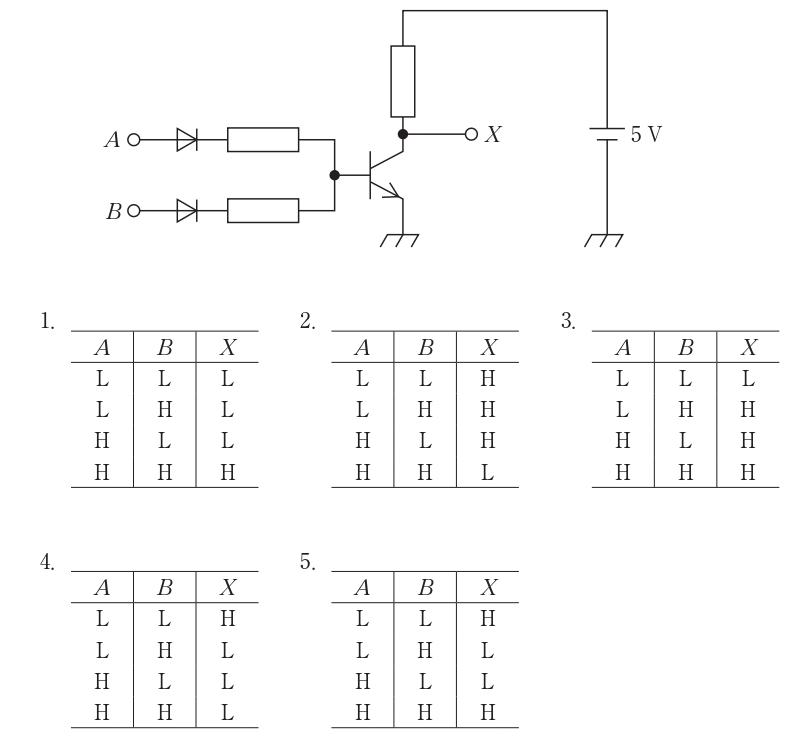
回路は、A・Bの各入力がダイオードと抵抗を介してNPNトランジスタのベースに接続され、出力Xはコレクタで5 Vにプルアップされている。AまたはBがH(5 V)のときは、ダイオードが順方向となってベース電流が流れ、トランジスタがONになりコレクタXは接地側へ引き下がってL(0 V)となる。A, Bの両方がL(0 V)のときのみトランジスタはOFFで、XはプルアップによりH(5 V)となる。よって真理値はLL→H、LH→L、HL→L、HH→Lで、論理式は$X=\overline{A+B}$(NOR)。対応する表は選択肢4である。
選択肢別解説
誤り。提示の表はAND回路(X=AB)の真理値表で、LL→L、LH→L、HL→L、HH→Hとなる。本回路は入力のダイオードORとトランジスタ反転の組合せであり、NOR動作となるため一致しない。
$誤り。表はAのみを反転した形(X=\overline{A})で、Bに依存しない。本回路はAまたはBがHならベース電流が流れてXがLとなるため、両入力に依存するNORであり一致しない。$
誤り。表はOR回路(X=A+B)の真理値表で、LL以外でX=Hとなる。実際の回路ではAまたはBがHでトランジスタがONとなりXはLになるため、ORとは逆(NOR)である。
正しい。A, BがいずれかHならベース電流が流れてトランジスタON→XはL。A, BがともにLならトランジスタOFF→プルアップ抵抗によりXはH。したがってLL→H、LH→L、HL→L、HH→Lとなり、NORの真理値表に一致する。
誤り。表は等価論理(XNOR)に相当し、入力が等しいときのみHとなる。本回路はNORであり、この表とは一致しない。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
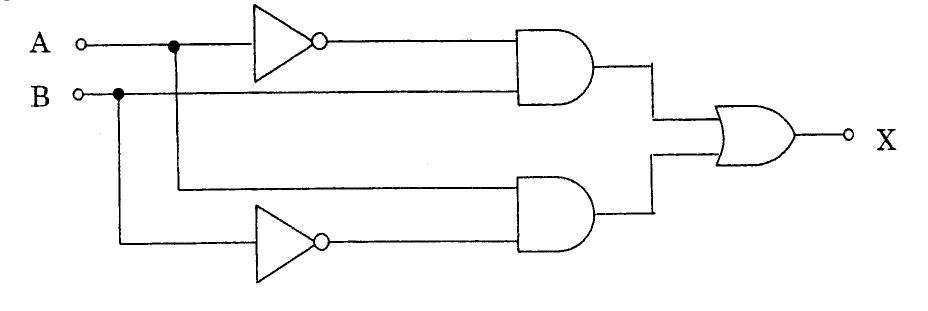
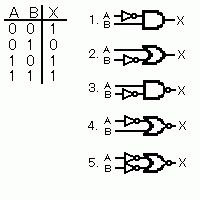
$真理値表では X は (A,B)=(0,1) のときだけ 0、その他は 1 である。主加法標準形は X=\bar{A}\bar{B}+A\bar{B}+AB で、整理すると X=\bar{B}+AB となる。吸収則の一形 P+P'Q=P+Q を用いれば X=\bar{B}+AB=\bar{B}+A、すなわち X=A+\bar{B}。したがって、A をそのまま、B を反転して OR ゲートに入れる回路が一致し、画像の選択肢2が該当する。$
選択肢別解説
$画像の回路1は A 入力に否定(バブル)、B はそのままを AND へ入力しているため、論理式は X=\bar{A}\cdot B。これは (A,B)=(0,1) のときのみ 1 となり、与えられた真理値表((0,1) のみ 0)とは一致しない。$
$画像の回路2は A をそのまま、B を否定して OR へ入力しているため、X=A+\bar{B}。真理値表では (0,1) のときのみ X=0、他は 1 であり、X=A+\bar{B} と完全に一致する。正答。$
$画像の回路3は A をそのまま、B を否定して AND に入力し、出力に否定(バブル)が付くため NAND。従って X=\overline{A\cdot \bar{B}}=\bar{A}+B(ド \cdot モルガン)。これは (A,B)=(1,0) のときのみ 0 となり、真理値表と一致しない。$
$画像の回路4は A に否定(バブル)、B はそのままを OR に入力し、出力に否定が付く NOR。よって X=\overline{\bar{A}+B}=A\cdot \bar{B}。これは (A,B)=(1,0) のときのみ 1 で、真理値表と一致しない。$
$画像の回路5は A と B の両方に否定(バブル)を付けて OR に入力し、出力に否定が付く NOR。従って X=\overline{\bar{A}+\bar{B}}=A\cdot B(ド \cdot モルガン)。これは (A,B)=(1,1) のときのみ 1 で、真理値表と一致しない。$
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
与式 $X=(A+B)\cdot(\overline{A}+B)$ は展開して整理すると $X=A\cdot\overline{A}+A\cdot B+\overline{A}\cdot B+B\cdot B$ となる。相補律 $A\cdot\overline{A}=0$、冪等律 $B\cdot B=B$ を用い、さらに $A\cdot B+\overline{A}\cdot B=(A+\overline{A})\cdot B=1\cdot B=B$(相補律と分配法則)より、結局 $X=0+B+B=B$ となる。一般形としても $(X+Y)\cdot(\overline{X}+Y)=Y$ が成り立つため、本問は $Y=B$ に相当し答えは $B$。
選択肢別解説
誤り。恒真式ではない。例えば $A=0,B=0$ で $X=(0+0)\cdot(1+0)=0\cdot1=0\neq1$。
誤り。簡単化結果は $B$。反例として $A=0,B=1$ のとき、$X=(0+1)\cdot(1+1)=1\cdot1=1$ だが $A=0$ で一致しない。
正しい。展開とブール代数の法則(分配法則、相補律 $A\cdot\overline{A}=0$, 冪等律 $B\cdot B=B$, 相補律 $A+\overline{A}=1$)から $X=B$ に簡単化される。
誤り。簡単化結果は $B$ であり $A\cdot B$ ではない。例えば $A=0,B=1$ で $X=1$ に対し $A\cdot B=0$。
誤り。簡単化結果は $B$。例えば $A=0,B=0$ では $X=0$ だが $\overline{A}\cdot\overline{B}=1$ となり一致しない。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
与式 $\overline{(A+B)}\cdot(\overline{A}+B)$ をブール代数で簡約する。まずド・モルガン則より $\overline{(A+B)}=\overline{A}\cdot\overline{B}$。よって $(\overline{A}\cdot\overline{B})\cdot(\overline{A}+B)$。分配則で展開すると $(\overline{A}\cdot\overline{B}\cdot\overline{A})+(\overline{A}\cdot\overline{B}\cdot B)$。べき等則により $\overline{A}\cdot\overline{A}=\overline{A}$、相補則により $\overline{B}\cdot B=0$ だから $(\overline{A}\cdot\overline{B})+(\overline{A}\cdot 0)=\overline{A}\cdot\overline{B}$。したがって等しいのは $\overline{A}\cdot\overline{B}$(選択肢5)である。
選択肢別解説
$\overline{A}$ ではない。例えば $A=0,\ B=1$ のとき,元の式は $\overline{(0+1)}\cdot(\overline{0}+1)=\overline{1}\cdot(1+1)=0\cdot1=0$ だが,$\overline{A}=1$ となり一致しない。
$\overline{B}$ ではない。例えば $A=1,\ B=0$ のとき,元の式は $\overline{(1+0)}\cdot(\overline{1}+0)=\overline{1}\cdot(0+0)=0\cdot0=0$ だが,$\overline{B}=1$ で一致しない。
$\overline{A}\cdot B$ ではない。例えば $A=0,\ B=1$ のとき,元の式は 0 となる一方,$\overline{A}\cdot B=1\cdot1=1$ で一致しない。
$A\cdot\overline{B}$ ではない。例えば $A=1,\ B=0$ のとき,元の式は 0 となるが,$A\cdot\overline{B}=1\cdot1=1$ で一致しない。
正しい。ド・モルガン則 $\overline{(A+B)}=\overline{A}\cdot\overline{B}$,分配則,べき等則,相補則を順に用いると $(\overline{A}\cdot\overline{B})\cdot(\overline{A}+B)=\overline{A}\cdot\overline{B}$ となる。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
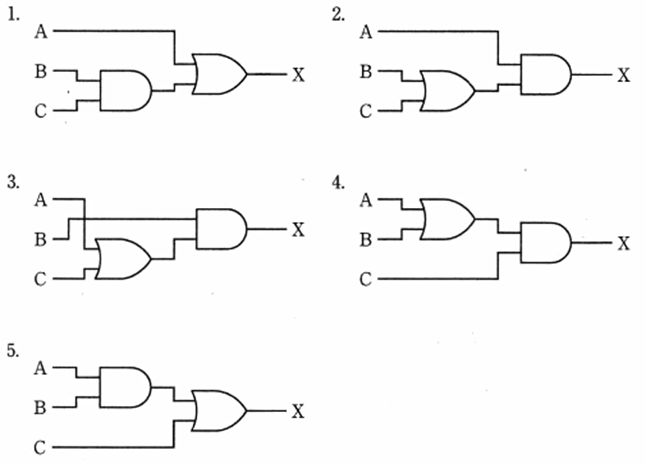
与えられた論理式 $X = A \cdot B + A \cdot C$ はブール代数の分配法則 $P \cdot Q + P \cdot R = P \cdot (Q + R)$ により $X = A \cdot (B + C)$ と等価である。したがって回路としては、まずBとCをORし、その出力とAをANDする構成になる。添付の回路図では2がこの構成に一致する。その他の選択肢はそれぞれ $A + B \cdot C$、$(A + C) \cdot B$、$(A + B) \cdot C$、$A \cdot B + C$ を実現しており、与式とは一致しない。
選択肢別解説
図1はBとCをANDし、その結果をAとORしているため、論理式は $X = A + B \cdot C$。与式 $A \cdot B + A \cdot C$ とは異なる。例えば $A=0, B=1, C=1$ では本回路は $0 + 1\cdot1 = 1$、与式は $0\cdot1 + 0\cdot1 = 0$ で不一致。
図2はBとCをORし、その出力をAとANDしているため、論理式は $X = A \cdot (B + C)$。分配法則により $A \cdot (B + C) = A \cdot B + A \cdot C$ で与式と等価。
図3はAとCをORし、その出力をBとANDしている構成に読めるため、論理式は $X = (A + C) \cdot B = A \cdot B + B \cdot C$。与式 $A \cdot B + A \cdot C$ とは異なる。例えば $A=1, B=0, C=1$ では本回路は $(1+1)\cdot0=0$、与式は $1\cdot0+1\cdot1=1$ で不一致。
図4はAとBをORし、その出力をCとANDしているため、論理式は $X = (A + B) \cdot C = A \cdot C + B \cdot C$。与式とは異なる。例えば $A=0, B=1, C=1$ では本回路は $(0+1)\cdot1=1$、与式は $0\cdot1+0\cdot1=0$ で不一致。
図5はAとBをANDし、その出力をCとORしているため、論理式は $X = A \cdot B + C$。与式とは異なる。例えば $A=0, B=1, C=1$ では本回路は $0\cdot1+1=1$、与式は $0\cdot1+0\cdot1=0$ で不一致。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
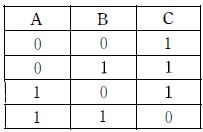
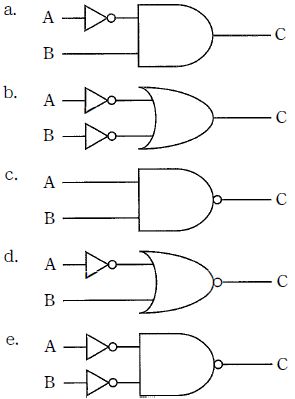
提示の真理値表は A,B の4組 (00,01,10,11) に対して出力Cが (1,1,1,0) となっている。これは「AとBがともに1のときだけ0、それ以外は1」を示し、論理式で $C=\overline{A\cdot B}$、すなわちNANDの真理値表である。したがってNANDそのもの、もしくはド・モルガンの定理で等価変換された回路が該当する。画像説明によれば、cはNANDゲートそのもの、bは $C=\overline{A}+\overline{B}=\overline{A\cdot B}$ に等価であり、いずれも真理値表を満たす。a,d,e は各々 $\overline{A}\cdot B$、$A\cdot \overline{B}$、$\overline{A}\cdot\overline{B}=\overline{A+B}$ で、いずれも表の出力パターンと一致しない。
選択肢別解説
$aは C=\overline{A}\cdot B(NOT A と B のAND)。A=0, B=0 のとき C=0 だが、真理値表は C=1 を要求するため一致しない。$
$bは C=\overline{A}+\overline{B}。ド \cdot モルガンの定理より C=\overline{A\cdot B} で、NANDと等価。真理値表 (00→1, 01→1, 10→1, 11→0) と完全一致する。$
$cは C=\overline{A\cdot B}(NANDゲートそのもの)。提示の真理値表と一致する。$
$dは C=\overline{\overline{A}+B}=A\cdot \overline{B}。A=0, B=0 のとき C=0 となり、真理値表の C=1 と一致しない。$
$eは C=\overline{A}\cdot \overline{B}=\overline{A+B}(NOR)。A=0, B=1 のとき C=0 だが、真理値表は C=1 を要求するため一致しない。$
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
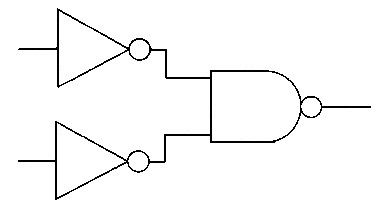
図の回路は、各入力A・BをそれぞれNOTで反転させた後、その2値をNANDに入力している。論理式で表すと出力Xは $X=\overline{\overline{A}\cdot\overline{B}}$。ド・モルガンの定理 $\overline{P\cdot Q}=\overline{P}+\overline{Q}$ を適用すると $X=\overline{\overline{A}}+\overline{\overline{B}}=A+B$ となり、OR(論理和)に等価である。したがって正答はOR。
選択肢別解説
正しい。回路の出力は $X=\overline{\overline{A}\cdot\overline{B}}=A+B$ となり、OR(論理和)に一致する。なお、選択肢の表記「0R」は論理ゲート名として一般的でなく、ORの誤記と考えられる。
誤り。ANDは $A\cdot B$。本回路は $A+B$ を実現するため、例えばA=1,B=0で本回路は1だがANDは0となり一致しない。
誤り。NORは $\overline{A+B}$。本回路は $A+B$ なので、A=B=0のとき本回路は0、NORは1となり一致しない。
誤り。NOTは1入力の反転器であり、図の回路は2入力の結合論理(OR)を実現しているため一致しない。
誤り。NANDは $\overline{A\cdot B}$。本回路は入力を反転してからNANDをとるため $\overline{\overline{A}\cdot\overline{B}}=A+B$ となり、NANDそのものではない。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
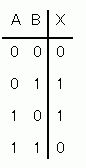
提示の真理値表は 00→0, 01→1, 10→1, 11→0 であり、入力AとBが異なるときのみ出力X=1となる。これは排他的論理和(Exclusive OR, XOR)に一致する。論理式としては $X=A\oplus B=\overline{A}B+A\overline{B}=(A+B)\,\overline{AB}$ と表せる。他の基本演算(AND, OR, NAND, NOR)は 11 または 00 の行での出力が一致せず、この表と合致しない。
選択肢別解説
ANDは両入力が1のときのみ1(00→0, 01→0, 10→0, 11→1)。提示表では 11→0 なので一致しない。
NANDはANDの否定で、両入力が1のときのみ0(00→1, 01→1, 10→1, 11→0)。提示表の 00→0 と異なるため不一致。
ORは少なくとも一方が1なら1(01→1, 10→1, 11→1)。提示表では 11→0 なので一致しない。
NORはORの否定で、両入力が0のときのみ1(00→1)。提示表は 00→0 のため一致しない。
Exclusive OR(XOR)は入力が異なるときのみ1(00→0, 01→1, 10→1, 11→0)。提示の真理値表と完全一致する。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
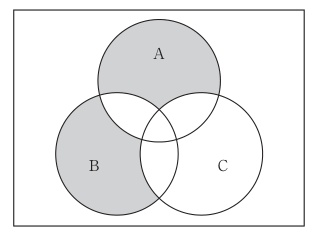
図の網掛けは、Aのみ、またはBのみに属する領域で、AとBの共通部分は含まず、さらにCに属する部分はすべて除外されている。したがって領域は $(A \oplus B) \cdot \overline{C}$ を表す。XOR は $(A+B)\cdot\overline{(A\cdot B)}$ と等価で、ド・モルガンの定理 $\overline{(A\cdot B)}=\overline{A}+\overline{B}$ を用いると $(A+B)\cdot(\overline{A}+\overline{B})\cdot\overline{C}$ となる。よって選択肢4が一致する。
選択肢別解説
$A\cdot\overline{B}\cdot C+\overline{A}\cdot B\cdot C=(A\oplus B)\cdot C$ を表し、Cに属する部分を含む。図ではC領域は網掛けされていないため不適。
$(A\cdot B+\overline{A}\cdot\overline{B})\cdot C$ は $A$ と $B$ の同値(XNOR)に $C$ を掛けた領域で、Cに属する部分のみを含む。図はCを含まないので不適。
$(A\cdot B+\overline{A}\cdot B)\cdot\overline{C}=B\cdot(A+\overline{A})\cdot\overline{C}=B\cdot\overline{C}$ に簡約され、Cを除いたB全域(ABの部分も含む)を示す。図では $A\cap B$ の部分は網掛けされていないため不一致。
$(A+B)\cdot(\overline{A}+\overline{B})\cdot\overline{C}$ は $(A\oplus B)\cdot\overline{C}$ に等価で、AまたはBに属するが両方には属さず、かつCには属さない領域。図の網掛けと一致する。
$(A+B)\cdot(\overline{A}+\overline{B})\cdot C=(A\oplus B)\cdot C$ であり、Cに属する部分を含む。図ではC領域は網掛けされていないため不適。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
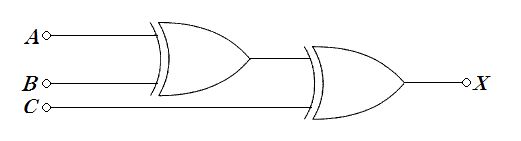
$図はXORを直列に2段接続した回路で、出力は X = (A \oplus B) \oplus C となる。XORは2入力が異なるとき1を出すため、3値に拡張したこの形は「1の個数が奇数のときX=1」となる奇数パリティ判定である。与えられた選択肢を計算すると、(A,B,C)=(0,0,1) と (1,1,1) でX=1となる。一方、参照情報および過去問の整合からは選択肢2は本来 (0,1,1) と考えられ、その場合はX=0で正答は選択肢5のみとなる。よって本問題のDBには選択肢2の誤記が疑われる。$
選択肢別解説
$A=0、B=0、C=0。計算: A \oplus B = 0 \oplus 0 = 0、ついで X = 0 \oplus 0 = 0。したがってXは0で、出力1にはならない。$
$A=0、B=0、C=1。計算: A \oplus B = 0、X = 0 \oplus 1 = 1。よってX=1となり、本来は出力1の条件に該当する。ただし、参照過去問ではこの選択肢は A=0、B=1、C=1 であり、その場合は X = (0\oplus1)\oplus1 = 1\oplus1 = 0 となる。DB側のBの値が誤記の可能性が高い。$
$A=1、B=1、C=0。計算: A \oplus B = 1 \oplus 1 = 0、X = 0 \oplus 0 = 0。したがってXは0。$
$A=1、B=0、C=1。計算: A \oplus B = 1 \oplus 0 = 1、X = 1 \oplus 1 = 0。したがってXは0。$
$A=1、B=1、C=1。計算: A \oplus B = 1 \oplus 1 = 0、X = 0 \oplus 1 = 1。したがってXは1となる。$
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
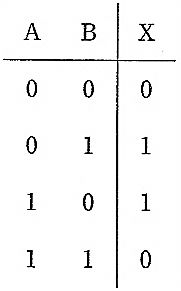
画像の真理値表は、A=0,B=0でX=0、A=0,B=1でX=1、A=1,B=0でX=1、A=1,B=1でX=0である。これは入力が異なるときのみ1になる排他的論理和に一致する。すなわち $X = A \oplus B = \overline{A}B + A\overline{B}$。AND, OR, NAND, NOR の各真理値表と照合するといずれも一致しないため、対応する論理演算はEXOR(exclusive OR)である。
選択肢別解説
AND(論理積)はAとBが両方1のときのみ出力1、その他は0。提示表では(1,1)でX=0なので一致しない。
NAND(否定論理積)は(1,1)のときだけ0で、それ以外は1。提示表は(0,0)でX=0となっており、NANDの(0,0)→1と矛盾する。
OR(論理和)は少なくとも一方が1なら出力1で、(1,1)でも1になる。提示表では(1,1)でX=0のため一致しない。
NOR(否定論理和)は(0,0)のときのみ1、その他は0。提示表では(0,1)や(1,0)でX=1となっておりNORとは一致しない。
EXOR(排他的論理和)は入力が異なるときのみ1、等しいとき0。提示表の(0,1),(1,0)で1、(0,0),(1,1)で0と完全に一致する。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。
解説
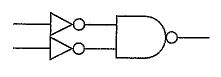
$図の回路は、各入力A \cdot Bを一度ずつNOTで反転し、その2本をNANDに入れている。論理式は X = \overline{\overline{A} \cdot \overline{B}} となる。ド \cdot モルガンの定理より \overline{\overline{A} \cdot \overline{B}} = A + B であり、最終的にOR(論理和)ゲートと等価である。したがって等価な回路はORである。$
選択肢別解説
$「0R」は表記誤りと考えられ、OR(論理和)を指すものと判断される。本回路は X = \overline{\overline{A} \cdot \overline{B}} = A + B となるため、ORに等価であり、この選択が正しい。$
$ANDは X = A \cdot B で表されるが、本回路の出力は X = A + B であり一致しないため不正解。$
$NORは X = \overline{A + B} であり、本回路の X = A + B とは一致しないため不正解。$
NOTは1入力1出力の否定回路だが、提示回路は2入力をとる等価OR回路であるため不正解。
$NANDは X = \overline{A \cdot B} である。提示回路は NAND(\overline{A}, \overline{B}) = A + B となり、NANDそのものではなくORに等価。$
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。

解説
提示された真理値表は、A,Bの3通り(00,01,10)で出力Xが1、A=B=1のときのみ0となる。これはANDの結果を否定した論理であり、式で書くと $X=\overline{A\cdot B}$。したがって対応する論理演算はNAND(否定論理積)である。
選択肢別解説
AND(論理積)は $X=A\cdot B$。A=B=1のときのみ1、他は0となる。提示表ではA=B=1で0なので一致しない。
OR(論理和)は $X=A+B$(少なくとも一方が1で1)。00のとき0、それ以外は1。提示表は00で1となっており一致しない。
XOR(排他的論理和)は入力が異なるときのみ1、同じときは0。よって00→0, 01→1, 10→1, 11→0。提示表は00で1となっており一致しない。
NOR(否定論理和)はORの否定で、00のときのみ1、その他は0。提示表では01や10で1となっているため一致しない。
NAND(否定論理積)はANDの否定で $X=\overline{A\cdot B}$。A=B=1のときのみ0、その他は1。提示表(00→1, 01→1, 10→1, 11→0)と完全一致する。
解説を表示するにはログインが必要です。ログインすると無料枠(1日5問)をご利用いただけます。
無料プランでは解説を1日5問まで表示できます。解説を表示すると残り回数が消費されます。
今日: 回 | 残り 回
本日の無料枠を使い切りました。プレミアム登録で無制限にご利用いただけます。