臨床工学技士問題表示
臨床工学技士国家試験
解説
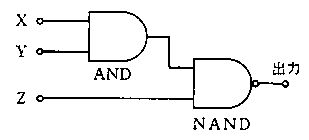
本問の論理は NAND（否定積）と解釈される論理演算 $\overline{X \cdot Y}$ を出力する回路である。NAND は真理値表で (X, Y) が (1,1) のときだけ 0、それ以外は 1 となる。図の入力から各区間の組み合わせは、t0–t1: (0,0)、t1–t2: (1,0)、t2–t3: (1,1)、t3–t4: (0,1)。したがって出力は順に 1, 1, 0, 1 となる。この波形（t0–t2 が 1、t2–t3 が 0、t3–t4 が 1）に一致するのは選択肢Bである。
選択肢別解説
A は t2 以降が 0 のままで、t3–t4 区間が 1 となるべき NAND の結果（1,1,0,1）と一致しない。
B は t0–t2 が 1、t2–t3 が 0、t3–t4 が 1 の波形であり、NAND 出力 $\overline{X \cdot Y}$ の結果と一致する。
C は t0–t1 で 0 となっており、この区間は (X,Y)=(0,0) なので NAND 出力は 1 であるはず。よって一致しない。
D は t1–t2 が 0 になっているが、この区間は (X,Y)=(1,0) で NAND は 1。したがって一致しない。
E は t3–t4 が 0 になっているが、この区間は (X,Y)=(0,1) で NAND は 1。よって一致しない。
解説
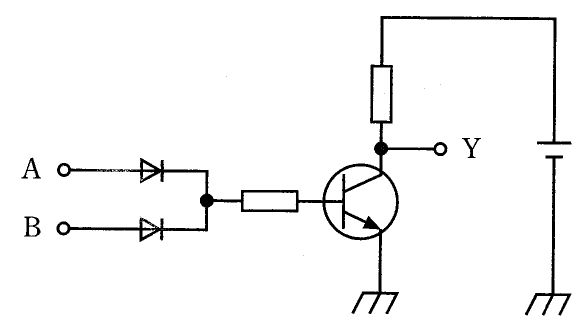
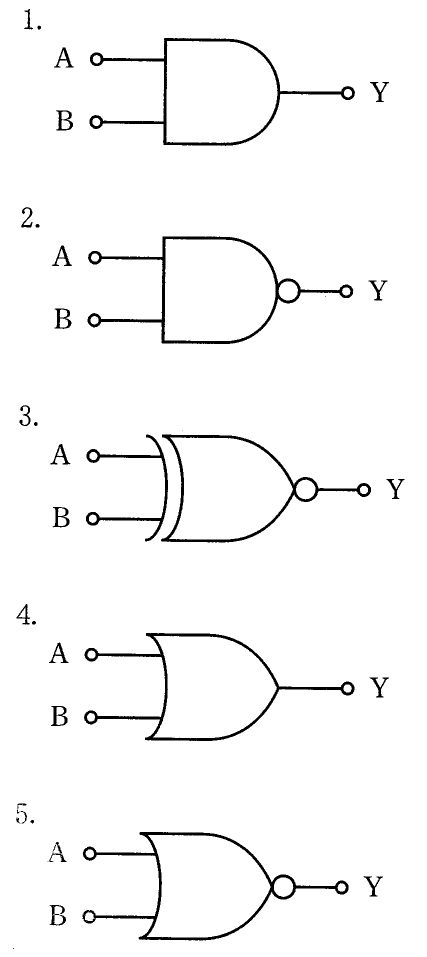
$与えられた回路はダイオードとトランジスタ（DTL）による論理回路で、正論理（H=1, L=0）で動作を考える。入力AまたはBのいずれかがHになると、入力側ダイオードを経てベースへ電流が流れトランジスタが導通し、コレクタ出力Yは抵抗を介してGND側へ引き込まれてLとなる。AとBがともにLのときのみベース電流が流れずトランジスタは遮断、コレクタはプルアップ抵抗でHとなる。従って真理値は「AまたはBが1ならY=0、A=B=0のときだけY=1」であり、これは論理和の否定であるNORの機能に一致する。式では Y=\overline{A+B}。MIL記号ではORゲートの出力側に否定を示すバブルが付いたシンボルがNORに相当する。$
選択肢別解説
$本回路の機能はY=\overline{A+B}（NOR）であり、AまたはBにHが入るとトランジスタが導通してYはL、A=B=LのときのみYがHとなる。この選択肢の論理はこれと一致しないため不正解。$
$本回路はダイオードで入力のいずれかがHのときベースに電流が流れてトランジスタがオン、出力YはLとなり、両入力がLのときのみYがHとなる。すなわちY=\overline{A+B}（NOR）。本選択肢は本回路と同じ機能ではないため不正解。$
$本回路はNOR動作（Y=\overline{A+B}）で、A=B=LのときのみH、AまたはBがHのときはLとなる。排他的論理などNOR以外の論理とは真理値が一致しないため不正解。$
$本回路の真理値はNOR（Y=\overline{A+B}）であり、入力のいずれかがHのとき出力はLになる。論理和そのもの（A+B）などNOR以外の論理とは一致しないため不正解。$
$本回路はAまたはBがHならトランジスタが導通してY=L、両方がLのときのみY=Hとなるため、論理和の否定であるNOR（Y=\overline{A+B}）に一致する。したがってこの選択肢が正解である。MIL記号ではORゲートの出力側に否定バブルが付いたシンボルが対応する。$
解説
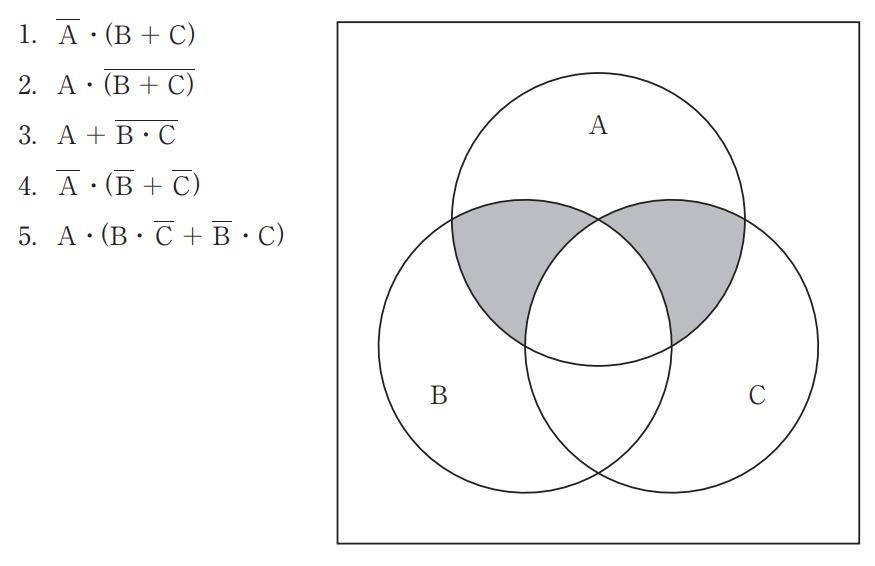
図の網掛けは、集合A内で「Bに属するがCには属さない部分」と「Cに属するがBには属さない部分」の和集合であり、三つの円の共通部分 A∩B∩C は除外されている。したがって論理式は $A\cdot(B\cdot\bar{C}+\bar{B}\cdot C)$、すなわち $A\cdot(B\oplus C)$ に一致する。これは A と B、C の排他的論理和の積で、ベン図の左右のレンズ形領域（A∩B∩\bar{C} と A∩\bar{B}∩C）をちょうど表す。
選択肢別解説
$\bar{A}\cdot(B+C)$ は A の外側で B または C に属する領域を表す。図の網掛けはすべて A の内部であるため一致しない。
$A\cdot\overline{(B+C)}$ は A に属し、かつ B にも C にも属さない部分（A 単独の部分）を表す。図では A∩B および A∩C の一部が網掛けで、A 単独は含まれないため不適。
$A+\bar{B}\cdot\bar{C}$ は A の全域に加え、B にも C にも属さない外側領域（\bar{B}\cdot\bar{C}）まで含む。図の網掛けは A 内の一部のみであり、外側領域や A の単独部分も含まないため不一致。
$\bar{A}\cdot(\bar{B}+\bar{C})$ は主に A の外側の領域を含む式で、図の網掛け（A 内のレンズ形部分）とは逆方向の領域となるため不適。
$A\cdot(B\cdot\bar{C}+\bar{B}\cdot C)$ は A∩B∩\bar{C}$ と $A∩\bar{B}∩C$ の和、すなわち A 内で B と C が排他的に成り立つ部分（$A\cdot(B\oplus C)$）を表す。図の左右のレンズ形網掛けと一致するため正しい。
解説
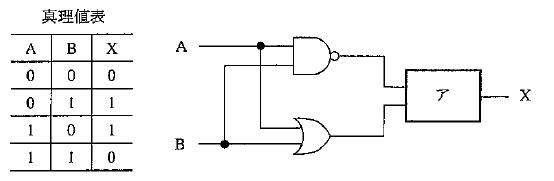
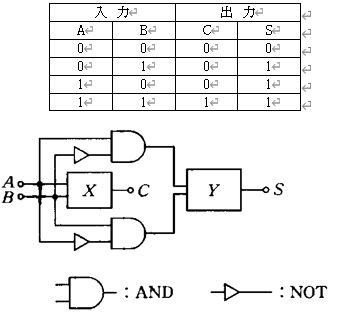
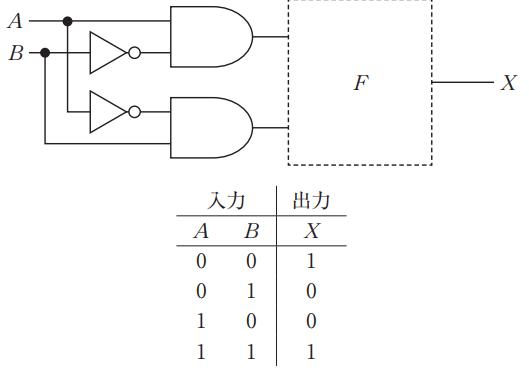
図の2つの前段ゲートはANDで、上段が $Y_1=A\overline{B}$、下段が $Y_2=\overline{A}B$ を出力する。これらは排他的論理和の積和形であり、和を取ると $Y_1+Y_2=A\oplus B$ となる。与えられた真理値表は $A=B$ のときに $X=1$ であり、すなわち $X=\overline{A\oplus B}$（XNOR）である。したがって $X=\overline{Y_1+Y_2}$ を実現する必要があり、FはNORが入る。
選択肢別解説
F=AND のとき $X=Y_1\cdot Y_2$。$Y_1=A\overline{B}$ と $Y_2=\overline{A}B$ は同時に1にならないため $Y_1\cdot Y_2=0$ となり、真理値表（00と11で1）に一致しない。
F=OR のとき $X=Y_1+Y_2=A\oplus B$ となる。これは 01,10 で1になるXORであり、与えられた真理値表（XNOR）と不一致。
F=NAND のとき $X=\overline{Y_1\cdot Y_2}=\overline{0}=1$ で常に1となり、01と10で0になる真理値表に合わない。
F=NOR のとき $X=\overline{Y_1+Y_2}=\overline{A\oplus B}$ となり、00と11で1、01と10で0の真理値表（XNOR）と一致する。
F=XOR のとき $X=Y_1\oplus Y_2$。$Y_1$ と $Y_2$ は排他的に1となるため $Y_1\oplus Y_2=Y_1+Y_2=A\oplus B$ であり、与えられた真理値表（XNOR）と一致しない。
解説
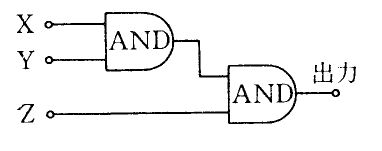
与えられた論理式はブール代数の分配則を用いて $AB + A\overline{B} = A(B + \overline{B})$ と変形できる。相補則より $B + \overline{B} = 1$ なので、式は $A\cdot 1 = A$ に簡略化される。したがって元の式が $1$ となる条件は $A=1$（かつ $B$ の値によらない）である。
選択肢別解説
正しい。$AB + A\overline{B}$ は分配則と相補則で $A(B+\overline{B})=A\cdot 1=A$ に等しい。よって式が $1$ となるのは $A=1$ のときである。
誤り。式は $A$ に等しいため、$B=1$ であっても $A$ が $0$ なら式は $0$。反例として $A=0, B=1$ では $AB + A\overline{B}=0\cdot 1 + 0\cdot 0=0$。
誤り。簡略化すると式は $A$ に等しく、$A$ の値に依存する。$A=1$ で $1$、$A=0$ で $0$ となるため「A、Bによらない」は成り立たない。
誤り。$A=0, B=1$ を代入すると $AB + A\overline{B}=0\cdot 1 + 0\cdot 0=0$ であり、$1$ とはならない。
誤り。$A=0, B=0$ を代入すると $AB + A\overline{B}=0\cdot 0 + 0\cdot 1=0$ であり、$1$ とはならない。
解説
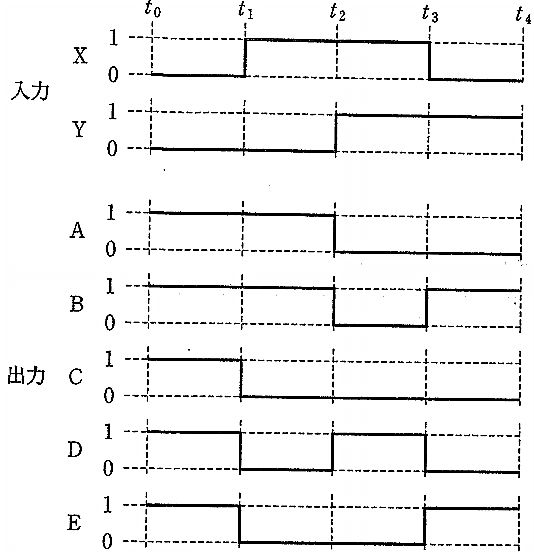
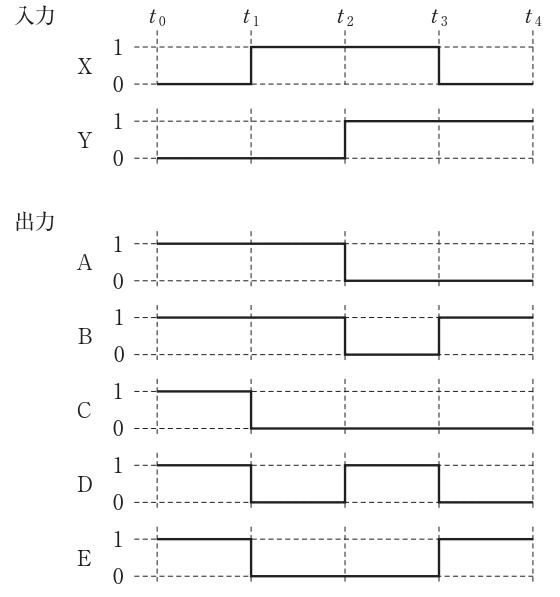
求める演算は NAND（否定論理積）であり、$\overline{X\cdot Y}$ は X と Y がともに1の区間だけ 0、それ以外は 1 となる。図の入力より、各時間区間の組は次の通り。
- t0〜t1: (X,Y)=(0,0) → $\overline{0\cdot 0}=1$
- t1〜t2: (1,0) → $\overline{1\cdot 0}=1$
- t2〜t3: (1,1) → $\overline{1\cdot 1}=0$
- t3〜t4: (0,1) → $\overline{0\cdot 1}=1$
よって出力は (1, 1, 0, 1) となり、図中の波形 B と一致する。
選択肢別解説
A は図から t0〜t2 が 1、t2〜t4 が 0 で (1,1,0,0)。NAND の出力 (1,1,0,1) と一致しない。
B は図から (1,1,0,1) を示す。これは $\overline{X\cdot Y}$ の結果と一致するため正解。
C は図から t0〜t1 が 1、t1 以降は 0 で (1,0,0,0)。NAND の (1,1,0,1) と一致しない。
D は図から (0,1,1,0)。NAND の (1,1,0,1) と一致しない。
E は図から t3〜t4 のみ 1 で (0,0,0,1)。NAND の (1,1,0,1) と一致しない。
解説
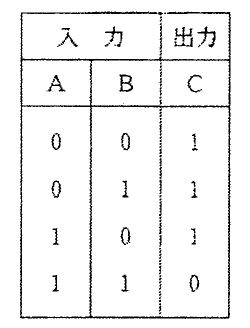
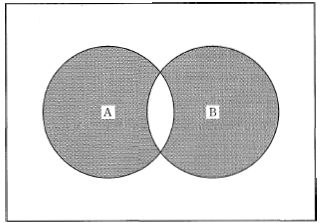
図の網掛けは、集合Aと集合Bのうち片方のみに属する領域（共通部分を除いた左右の部分）である。これは排他的論理和XORに相当し、論理式では $A \oplus B = A \cdot \overline{B} + \overline{A} \cdot B$ と表される。ORであれば重なりも含めてAとBの和集合全体が網掛けになるが、図では共通部分が白抜きであるため一致しない。ANDは共通部分のみが網掛けになる図となるが、これとも一致しない。
選択肢別解説
AND（論理積）は $A \cdot B$ で、AとBの共通部分のみが網掛けになるはずである。図は共通部分が網掛けではないため該当しない。
OR（論理和）は $A + B$ で、AまたはBに属する全体（重なり部分を含む和集合）が網掛けになる。しかし図では重なりが白抜きであり一致しない。
NOT（否定）は単一入力の演算で、例えば $\overline{A}$ のようにAの外側を指す。2入力A・Bの特定の部分（対称差）を示す本図を表せない。
XOR（排他的論理和）は $A \oplus B = A \cdot \overline{B} + \overline{A} \cdot B$。AとBのどちらか一方のみに属する部分が網掛けとなり、図と一致する。入力が異なるときのみ1となる性質を持つ。
NOR（否定論理和）は $\overline{A + B}$ で、AにもBにも属さない外部領域（長方形内の円の外側）が網掛けになる。図とは一致しない。
解説
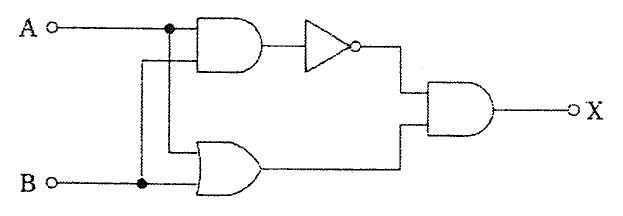
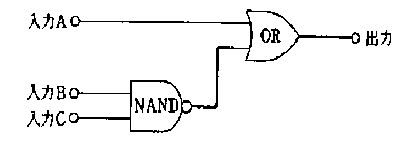
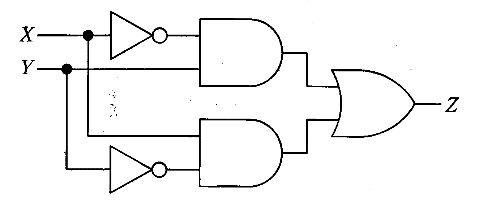
図の回路は、X と Y をそれぞれ反転した信号と元の信号を組み合わせた2つの AND の出力を OR でまとめている。論理式は $Z=\overline{X}\cdot Y + X\cdot \overline{Y}$ で、これは排他的論理和 (XOR) に一致する。XOR は入力が異なるときにのみ 1、等しいときは 0 となるため、常に $Z=1$ となる条件は「$X \neq Y$」である。
選択肢別解説
X=1 のとき、Y=1 なら $Z=\overline{1}\cdot 1 + 1\cdot \overline{1}=0$ となり 1 ではない。従って常に1とはいえない。
Y=1 のとき、X=1 なら $Z=\overline{1}\cdot 1 + 1\cdot \overline{1}=0$ となり 1 ではない。従って常に1とはいえない。
$X=Y$（00 または 11）のとき、式 $Z=\overline{X}\cdot Y + X\cdot \overline{Y}$ はどちらの積項も 0 となり $Z=0$。よって常に1ではない。
$X \neq Y$（01 または 10）のとき、$Z=\overline{X}\cdot Y + X\cdot \overline{Y}$ のいずれか一方の積項が 1 になり $Z=1$。したがって条件として正しい。
回路は XOR であり、入力の組合せに依存して 0/1 が変化する。例えば $X=Y$ では $Z=0$ となるため、入力によらず常に1ではない。
