第36回国試午後81問の類似問題

図のように鋼製丸棒に引張り荷重pをかけた。直径dを2倍にしたときの荷重方向の伸びは直径dのときの何倍か。（医用機械工学）

1: $\frac{1}{4}$

2: $\frac{1}{2}$

3: 1

4: 2

5: 4

長さ60cm、直径15mmの円柱に1000Nの圧縮力を加えたとき、長さが1mm短縮した。同じ材料の長さ40cm、直径10mmの円柱に1000Nの圧力を加えたとき、長さはおおよそ何mm短縮するか。

1: 1.5

2: 1

3: 0.75

4: 0.5

5: 0.25

長さ１ｍ、直径20ｍｍの円柱に1000Ｎの圧縮力を加えたとき、長さが２ｍｍ短縮した。同じ材料の、長さ50ｃｍ、直径10ｍｍの円柱に1000Ｎの圧縮力を加えたとき、長さはおよそ何ｍｍ短縮するか。

1: 4

2: 2

3: 1

4: 0.5

5: 0.25

図のように長さL、直径dの丸棒に加重Pを加えたところ、丸棒は∠Lだけ長くなり、∠dだけ紬くなった。正しいのはどれか。

a: 丸棒に曲げモーメントPLが作用する。

b: ヤング率はP/ΔLである。

c: 平均引張応力は4P/πd2である。

d: 軸方向の引張ひずみはΔL/Lである。

e: ポアソン比はΔL/Δdである。

1. a b　2. a e　3. b c　4. c d　5. d e

断面積Aの円柱状の棒を力Fで引っ張ると伸びるが、力を除くと元の状態に戻る。引張応力について正しいのはどれか。

1: Aに比例し、Fに反比例する。

2: Aに反比例し、Fに比例する。

3: AおよびFに比例する。

4: Fに比例し、Aには依存しない。

5: 棒の性質に依存する。

断面積が1cm2 で長さ10mの棒を1kNの力で引っ張ったとき、棒が0.5mm伸びた。この棒の弾性係数［GPa］はどれか。

1: 1

2: 2

3: 3

4: 4

5: 5

長さ1mの鋼材に10 kNの引張り荷重を加えたとき1mm 伸びた。この鋼材の断面積[mm2]はどれか。ただし、鋼材のヤング率は200GPaとする。

1: 2

2: 5

3: 20

4: 50

5: 200

断面積100mm2、長さ1mの鋼材に10kNの引張り荷重を加えたときの伸びはどれか。ただし、鋼材のヤング率に200GPa とする。

1: 0.1mm

2: 0.5mm

3: 1mm

4: 5mm

5: 10mm

長さ600mm、直径40mm の丸棒の長さ方向に荷重を加えたところ、長さが30μm 増加し、直径が0.76μm 減少した。この材料のポアソン比はどれか。

1: 0.0017

2: 0.025

3: 0.067

4: 0.14

5: 0.38

長さ1.2m、断面積4.0mm2の線材を8.0Nの力で引っ張ったところ長さが1.2mm増加した。この線材の縦弾性係数[GPa]はどれか。

1: 2

2: 5

3: 20

4: 50

5: 200

長さL、断面積Aが一様な丸棒の両端を力Pで圧縮したとき、長さがΔL短くなった。正しいのはどれか。

a: Pを圧縮荷重という。

b: P/Aを圧縮応力という。

c: 圧縮を中止しても、棒が元の長さに戻らない性質を塑性という。

d: 丸棒の中で一様に働く圧縮力は2Pになる。

e: ΔL/Lをボァソン比という。

1. a b c　2. a b e　3. a d e　4. b c d　5. c d e

図のように断面積が10cm2と50cm2の2本のピストン管をつなぎ、細いピストンに10Nの力を加えた。ピストンを静止させるために必要な力F[N]はどれか。

1: 2

2: 10

3: 50

4: 100

5: 250

図のように断面積が10cm2と50cm2の2本のピストン管をつなぎ、細いピストンに10Nのカを加えた。太いピストンに生じるカFはどれか。

1: 2N

2: 10N

3: 50N

4: 250N

5: 500N

丸棒がA点でピン支持されている。棒のC、D点にそれぞれ下向きに10N、20Nの力が加わっているとき、棒を水平に保持するためにB点に上向きに加える力Fはどれか。ただし、丸棒の重さは無視できる。

1: 50N

2: 100N

3: 200N

4: 300N

5: 500N

質量1.0 kg の剛体の棒が自由に回る継手を介して壁に取り付けられている。継手から0.30 m の所に質量1.0 kg の物体を置いた。棒が水平で動かないとき、継手から0.050 m の所に取り付けたひもが鉛直方向に引っ張るおよその力F［N］はどれか。ただし、棒の重心の位置は継手から0.15 m の所である。

1: 2

2: 5

3: 10

4: 20

5: 88

長さ1.0mの質量を無視できる棒がある。棒の中点を支点(回転軸)としで、鉛直面内で自由に回転できるようにした。図のように、棒の片端に質量100gの重りを取りつけ、棒を水平面から60°傾けたときに、棒に働く回転モーメントのおよその大きさ[Nm]はどれか。 

1: 0.025 

2: 0.05 

3: 0.1 

4: 0.25 

5: 0.5 

図に示す円筒状の物体に力Ｆが作用したとき、誤っているのはどれか。

a: 応力は物体の断面積Aが大きいほど小さい。

b: 応力とひずみが比例する性質をポアソンの法則という。

c: 引っ張りひずみとは変形前後の物体の長さの比である。

d: 引っ張りひずみとヤング率との積は応力に等しい。

e: 弾性限度以上の応力を加えると力を取り除いた後も変形が残る。

1. a b　2. a e　3. b c　4. c d　5. d e

断面積Aの材料に張カPを加えて引っ張った。正しいのはどれか。（医用機械工学）

1: 荷重方向と直交する方向に変形する割合をせん断ひずみという。

2: 材料はポアソン比分だけ荷重方向に伸びる。

3: 材料に発生する応力はP/Aである。

4: ポアソン数は発生したひずみにポアソン比を乗じた値である。

5: 発生したひずみを張力Pで割った値を弾性係数という。

直径60mm、長さ300mm のナイロン製の棒材が長軸方向に一様に圧縮されて1.5mm短縮したときの直径の増大分[mm]はどれか。ただし、ナイロンのポアソン比は0.4とする。　(医用機械工学)

1: 0.012

2: 0.075

3: 0.12

4: 0.6

5: 0.75

正しいのはどれか。

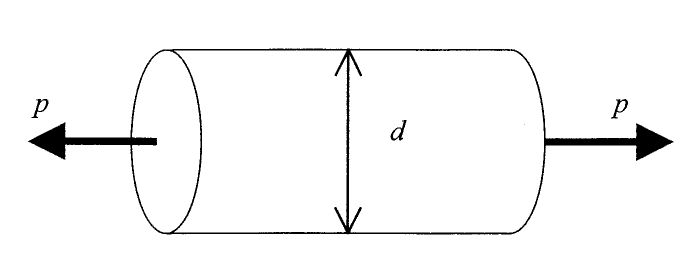
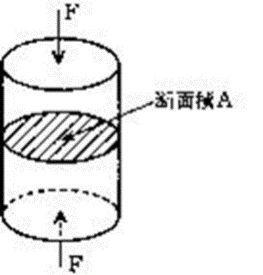
a: 外力により物体内部に生じる単位面積当たりの力を応力という。

b: 外力により生じた長さの変化量を変形前の長さで割った値をひずみという。

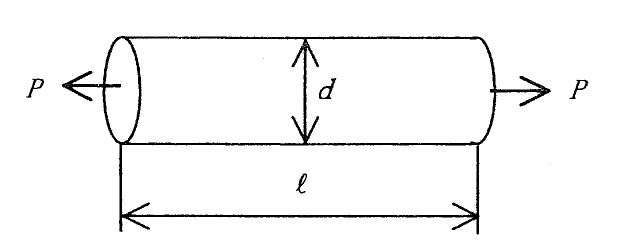
c: 太さが一様な丸棒にかかる応力をその結果生じるひずみで割った値をポアソン比という。

d: 弾性係数は単位の応力を与えるひずみである。

e: 切り欠けのある材料が外力に対して破壊しやすいのは応力集中を生じるためである。

1. a b c　2. a b e　3. a d e　4. b c d　5. c d e