第15回国試午後9問の類似問題

正しいのはどれか。

a: 水晶振動子を用いた発振回路は周波数安定度が高い。

b: 演算増幅器では発振回路を実現できない。

c: 発振には負帰還が必要である。

d: LC発振回路ではインダクタンスと静電容量の値で発振周波数が決まる。

e: 無安定マルチバイブレータは発振回路である。

1. a b c　2. a b e　3. a d e　4. b c d　5. c d e

図のような CR 直列回路に連続した方形波を入力させたときについて正しいのはどれか。

1: 抵抗の両端電圧 vR は積分波形を示す。

2: 回路の時定数は 0．47 ns である。

3: パルス幅に対して時定数は十分小さい。

4: vi~= R・i と表すことができる。

5: キャパシタの両端電圧 vC の波形はほぼ三角波となる。

正しいのはどれか。

a: 水晶振動子を用いた発振回路は周波数安定度が高い。

b: オペアンプでは発振回路を実現できない。

c: 発振には負帰還が必要である。

d: 双安定マルチバイブレータは発振回路である。

e: LC発振回路ではインダクタンスと静電容量の値で発振周波数が決まる。

1. a b　2. a e　3. b c　4. c d　5. d e

図の回路について正しいのはどれか。ただし、ダイオードﾞは理想的とし、入力電圧圧Viは周波数50Hz振幅1Vの正弦波とする。

1: ダイオードにかかる電圧の最大値は約2Vである。

2: ダイオードに流れる電流は正弦波である。

3: コンデンサにかかる電圧の最大値は約1.4Vである。

4: コンデンサにかかる電圧は正弦波である。

5: 抵抗を1kΩに変えるとコンデンサにかかる電圧のリップル(変動量)は減少する。

図の回路について誤っているのはどれか。 

a: 時定数は1msである。 

b: 遮断周波数は約160Hzである。 

c: 遮断周波数より十分に高い周波数では積分回路として動作する。 

d: 遮断周波数で出力電圧は入力電圧の1/2に減衰する。 

e: 入出力電圧の位相差は周波数によらず一定である。 

1. a b　2. a e　3. b c　4. c d　5. d e

インダクタンス10mHに正弦波交流電流2√2sin(120πt)[A]が流れている。正しいのはどれか。

a: 電流の実効値は2Aである。

b: 電流の周波数は60 Hz である。

c: インダクタンスの両端に発生する電圧の実効値は20mVである。

d: インダクタンスの両端に発生する電圧は電流より位相がπ/2rad遅れる。

e: インダクタンスの消費電力は0Wである。

1. a b c　2. a b e　3. a d e　4. b c d　5. c d e

図の回路について誤っているのはどれか。

a: 遮断周波数で出力電圧の減衰が最も大きい。

b: 遮断周波数は約160Hzである。

c: 時定数は1msである。

d: 遮断周波数より十分に高い周波数では積分回路として動作する。

e: 入出力電圧の位相差は周波数によらず一定である。

1. a b　2. a e　3. b c　4. c d　5. d e

図の回路の交流電源の周波数fを変化させたとき、電流iの振幅について正しいのはどれか。ただし、回路の共振周波数をfoとする。

1: fo付近ではfに比例する。

2: fo付近ではfに反比例する。

3: fo/$\sqrt2$ から$\sqrt2$fo の間で一定となる。

4: foで最大となる。

5: foで最小となる。

図1の回路に図2の正弦波電圧を印加した。D1に電流が流れる時間帯はどれか。ただし、ダイオードは理想ダイオードとする。（電子工学）

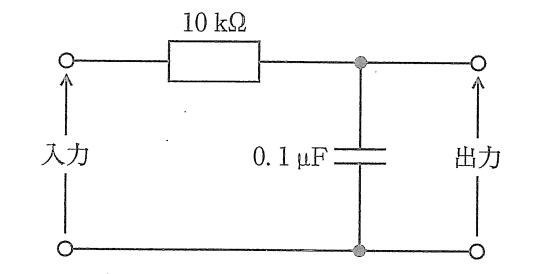
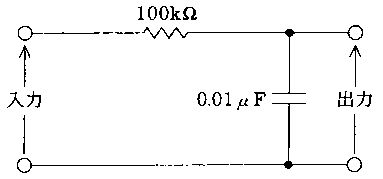
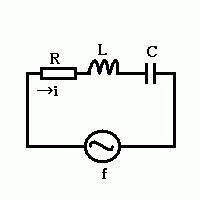
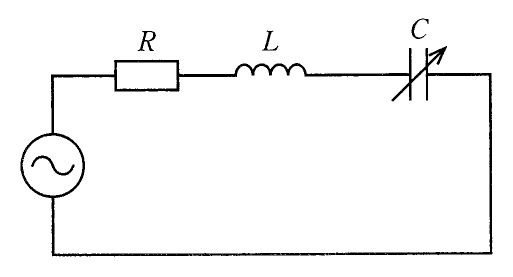
図の回路のインピーダンスの絶対値はどれか。ただし、ωは角周波数である。

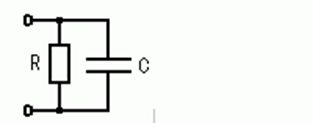
1: $ \sqrt {R+\frac {1}{\omega ^{2}c^{2}}}$

2: $ \sqrt {R^{2}+\omega ^{2}c^{2}}$

3: $ \frac {1}{\sqrt {R^{2}+\omega ^{2}c^{2}}}$

4: $ \sqrt {\frac {1}{1+\omega ^{2}c^{2}\pi ^{2}}}$

5: $\frac {1}{\sqrt {1+\omega ^{2}c^{2}R^{2}}}$

図の正弦波交流電圧波形について正しいのはどれか。

a: 周波数は 50 Hz である。

b: 角周波数は 50π rad/s である。

c: 周期は 10 ms である。

d: 電圧の平均値は 110 V である。

e: 電圧の実効値は 100 V である。

1. a b　2. a e　3. b c　4. c d　5. d e

インダクタンス10mHに正弦波交流電流$2\sqrt2sin{\left(120\pi t\right)}$〔A〕が流れている。正しいのはどれか。

a: 電流の実効値は2Aである。

b: 電流の周波数は60Hzである。

c: インダクタンスの両端に発生する電圧の実効値は20mVである。

d: インダクタンスの両端に発生する電圧は電流より位相が遅れる。

e: インダクタンスの消費電力は0Wである。

1. a b c　2. a b e　3. a d e　4. b c d　5. c d e

図の正弦波交流回路（f＝50 Hz）で静電容量が10μFのとき電流が最大になった。Lの値[H]に最も近いのはどれか。ただし、π2はおよそ10である。

1: 0.01

2: 0.1

3: 1

4: 10

5: 100

キャパシタに正弦波電圧を印加した場合、キャパシタの両端にかかる電圧と流れる電流との位相について正しいのはどれか。

1: 電圧は電流よりπ/2位相が遅れている。

2: 電圧は電流よりπ/4位相が遅れている。

3: 電圧は電流と同位相である。

4: 電圧は電流よりπ/4位相が進んでいる。

5: 電圧は電流よりπ/2位相が進んでいる。

正しいのはどれか。

a: 正帰還回路は発振回路に用いられる。

b: 直流増幅回路は直流成分だけを増幅する回路である。

c: 負帰還をかけると周波数特性が悪くなる。

d: 負帰還をかけると増幅度が大きくなる。

e: 水晶発振回路はRC発振回路よりも周波数安定度が高い。

1. a b　2. a e　3. b c　4. c d　5. d e

図の回路について、正しいのはどれか。ただし、Aは理想演算増幅器とする。

a: 時定数は20 msである。

b: 通過域での増幅度は20 である。

c: 直流成分はカットされる。

d: コンデンサC1と抵抗R2に流れる電流は等しい。

e: 入力インピーダンスは抵抗R1とR2で決まる。

1. a b　2. a e　3. b c　4. c d　5. d e

正弦波電圧（V　sin2πft）について正しいのはどれか。

a: 電圧の実効値はV/2である。

b: 抵抗Rに電圧を印加したとき消費される平均電力はRV2/2である。

c: インダクタンスLのコイルに電圧を印加したとき、流れる電流の最大振幅はV/(2πfL)である。

d: 静電容量Cのコンデンサに電圧を印加したとき、流れる電流の最大振幅は2πfCVである。

e: コンデンサに電圧を印加したとき、流れる電流の位相は電圧の位相と同じである。

1. a b　2. a e　3. b c　4. c d　5. d e

図の回路で正しいのはどれか。

1: 時定数は$\frac{1}{CR}$である。

2: 低域(通過)フィルタとして動作する。

3: 入力電圧の周波数が0に近づくと入力電圧と出力電圧の位相差は0に近づく。

4: コンデンサに流れる電流は入力電圧より位相が遅れる。

5: 遮断周波数では出力電圧の振幅は入力電圧の振幅のである。

図の波形について正しいのはどれか。

a: 周期は1sである。

b: 実効値は$1/\sqrt2$である。

c: 直流成分を含む。

d: 調波成分を含む。

e: 間tで微分すると三角波が得られる。

1. a b c　2. a b e　3. a d e　4. b c d　5. c d e

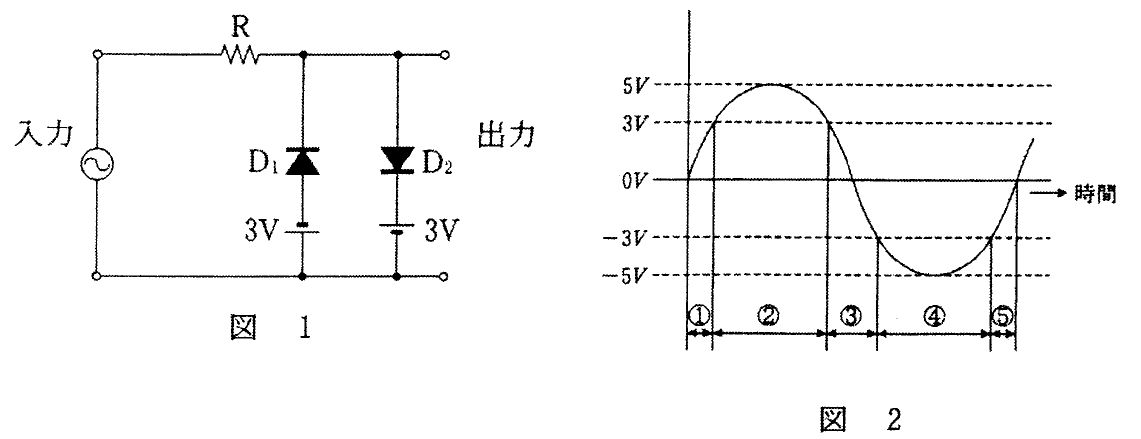
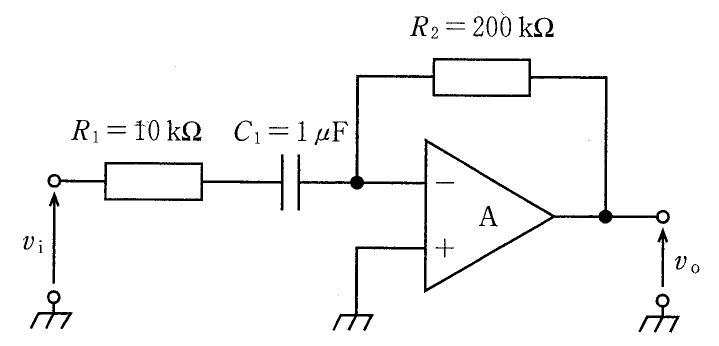
図の回路に、周波数fの正弦波電圧viを入力した。出力電圧voについて正しいのはどれか。ただし、Aは理想演算増幅器、fo = 1 / 2πCfRf とする。

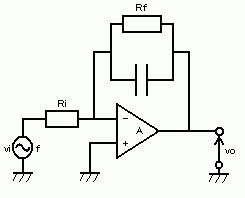
a: fがfoより十分小さければ vo = -(Rf/Ri) vi となる。

b: fがfoより十分大きければ vo = -(Rf/Ri)vi となる。

c: f = fo でvoの振幅は最大となる。

d: fがfoより十分小さければvoの振幅は0に近づく。

e: fがfoより十分大きければvoの振幅は0に近づく。

1. a b　2. a e　3. b c　4. c d　5. d e