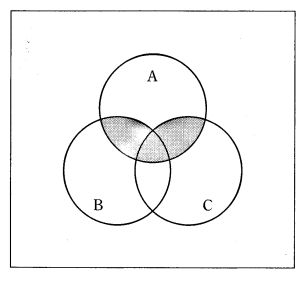
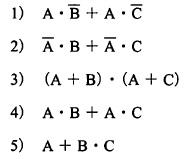第13回国試午後23問の類似問題
国試第9回午後:第29問
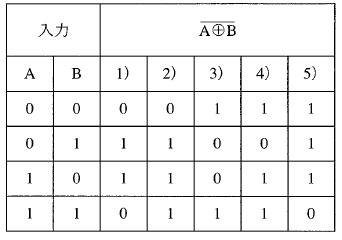
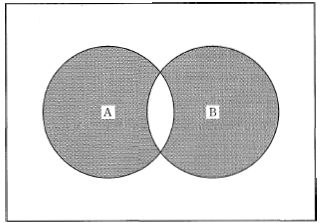
論理演算で正しいのはどれか。$\left(\overline{X+Y}\right)\bullet\left(\overline{X\bullet{Y}}\right)=$
1: $X\bullet\overline{Y}$
2: $\overline{X}\bullet{Y}$
3: $\overline{X}\bullet\overline{Y}$
4: $X\bullet{Y}$
5: $\overline{X}+\overline{Y}$
国試第17回午後:第20問
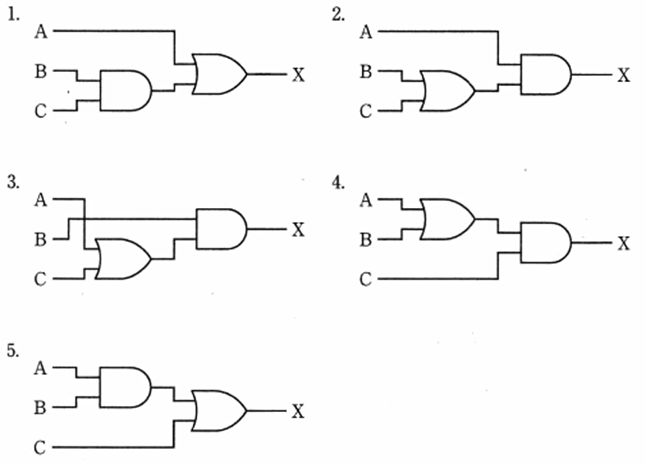
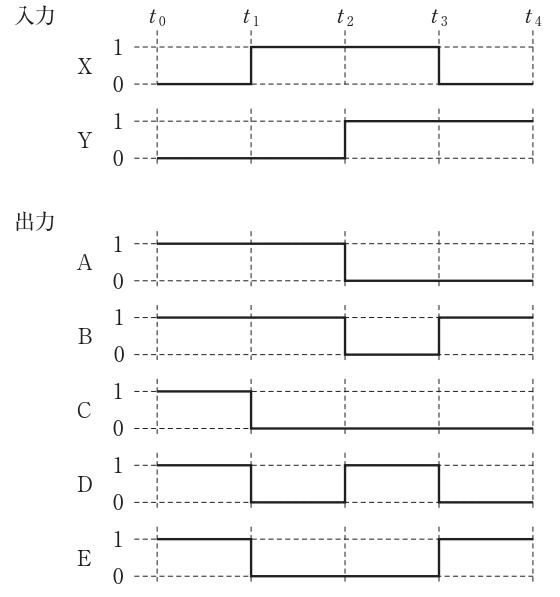
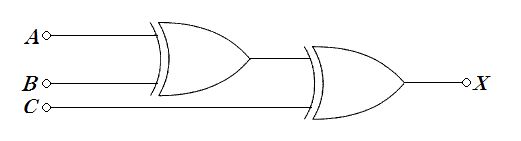
図の出力として正しいのはどれか。
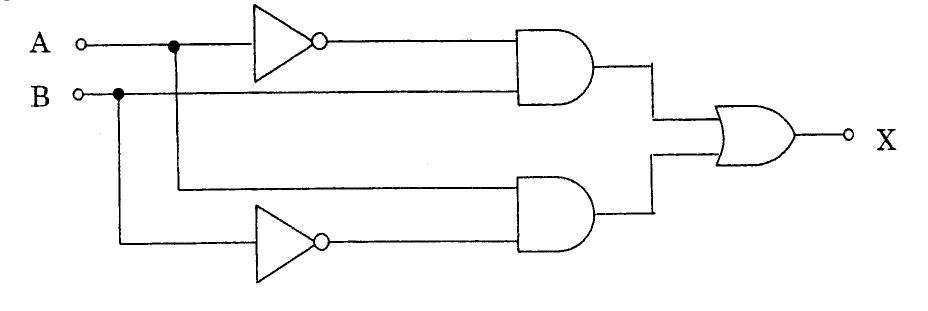
1: $X=\overline {A}\cdot \overline {B}+A\cdot B$
2: $X=\overline {A}\cdot B+A\cdot \overline {B}$
3: $X=\left( A+B\right) \cdot \left( A+\overline {B}\right) $
4: $X=\left( \overline {A}+B\right) \cdot \left( A+\overline {B}\right)$
5: $X=\overline {A}\cdot \left( A+B\right) +B\left( \overline {A}+\overline {B}\right)$