臨床工学技士問題表示
臨床工学技士国家試験
検索元問題
第11回 午後 第21問
20件の類似問題
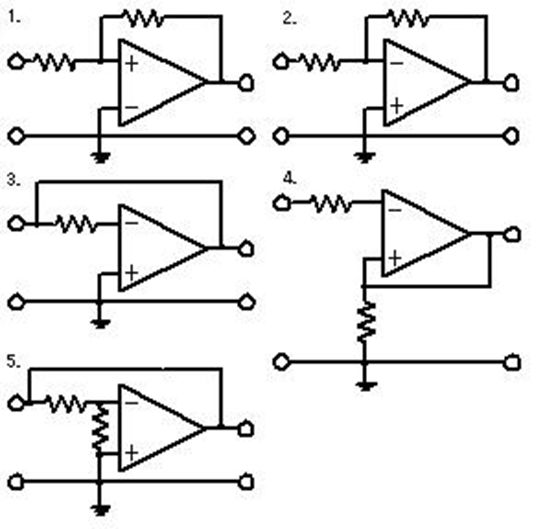
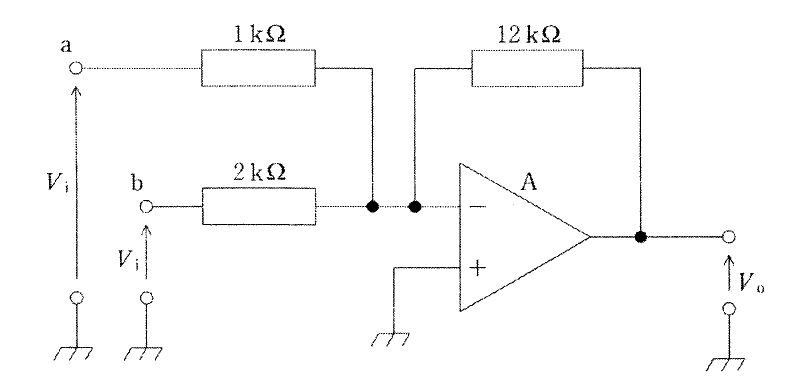
真理価表を実現する図の回路(半加算器)において、二つの論理素子(X、Y)はどれか。...
広告
48
臨床工学技士国家試験 -
第33回 午後
正答率:62%
類似度 55.2%
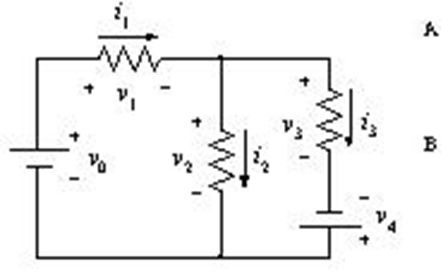
図の回路で成立するのはどれか。
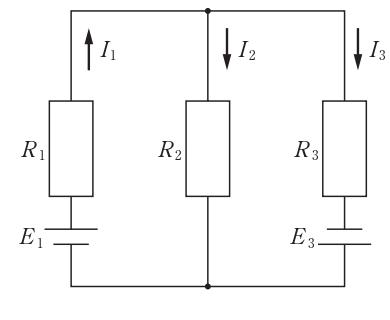
a
I 1 - I 2 - I 3 = 0
b
I 1 + I 2 + I 3 = E 1 /R 1
c
I 1 R 1 + I 3 R 3 = E 1 - E 3
d
I 1 R 1 + I 2 R 2 = E 1
e
-I 2 R 2 + I 3 R 3 = E 3
組み合わせ:
1. a b c
2. a b e
3. a d e
4. b c d
5. c d e
52
臨床工学技士国家試験 -
第28回 午後
正答率:75%
類似度 55.1%
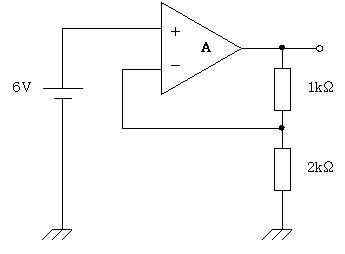
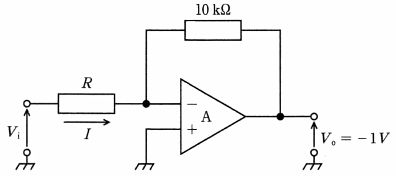
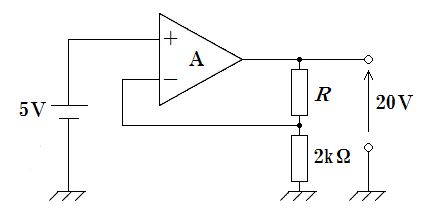
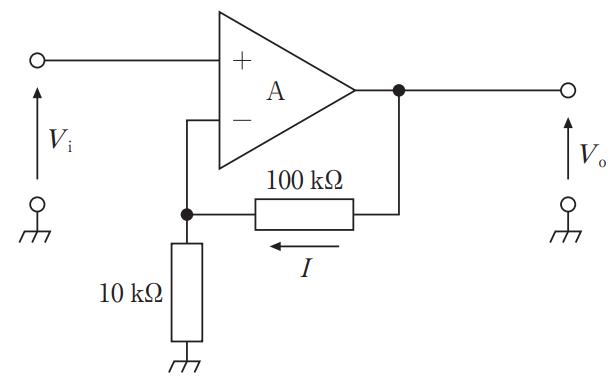
図の回路は、電圧増幅度 26 dB、入力抵抗 100 kΩ の増幅回路である。抵抗 R1と R2 の組合せはどれか。ただし、Aは理想演算増幅器で、log10 2 = 0.3 とする。
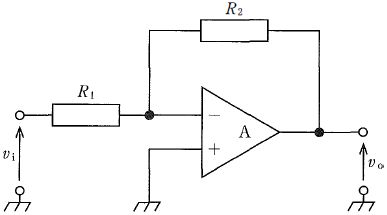
1
R1 = 5 kΩ、 R2 = 100 kΩ
2
R1 = 100 kΩ、 R2 = 1 MΩ
3
R1 = 100 kΩ、 R2 = 2 MΩ
4
R1 = 200 kΩ、 R2 = 4 MΩ
5
R1 = 200 kΩ、 R2 = 6 MΩ
広告
48
臨床工学技士国家試験 -
第22回 午前
正答率:62%
類似度 54.8%
図の回路で正しい式はどれか。
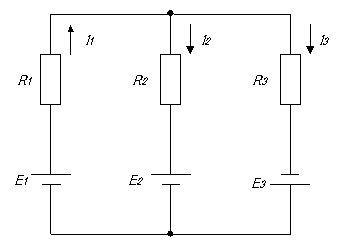
a
I1-I2-I3 = 0
b
I1+I2+I3 = E1/R1
c
I1・R1+I3・R3 = E1-E3
d
I1・R1+I2・R2 = E1-E2
e
-I2・R2+I3・R3 = E2+E3
組み合わせ:
1. a b c
2. a b e
3. a d e
4. b c d
5. c d e
広告
53
臨床工学技士国家試験 -
第24回 午後
正答率:51%
類似度 54.2%
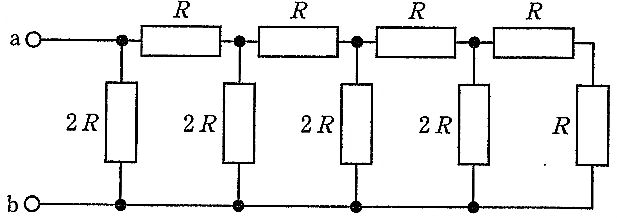
図の回路の入力インピーダンスはどれか。ただし、Aは理想演算増幅器、jは虚数単位、ωは角周波数とする。(医用電気電子工学)
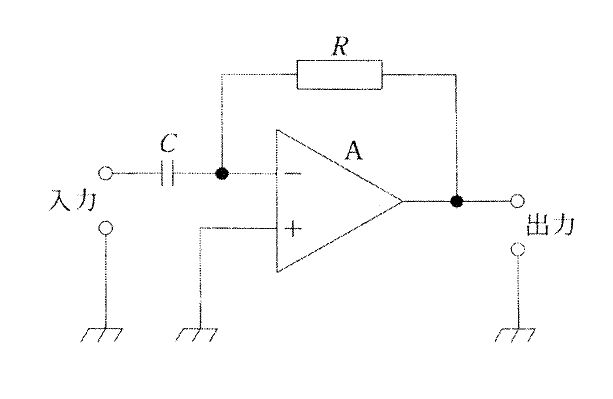
1
$ j\omega C$
2
$ \frac {1}{j\omega C}$
3
$ j\omega CR$
4
$ \frac {1}{j\omega CR}$
5
$ R+\frac {1}{j\omega C}$
59
臨床工学技士国家試験 -
第37回 午前
類似度 54.0%
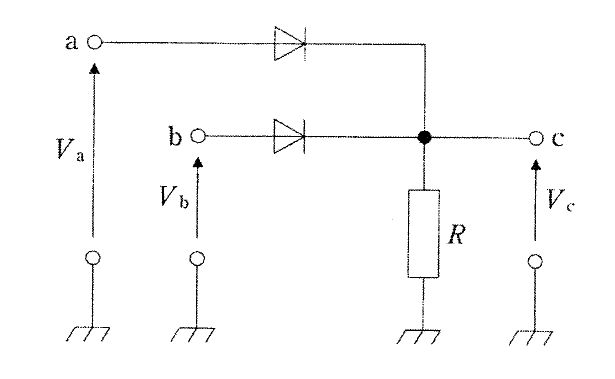
図の網掛け部分を表す論理式はどれか。
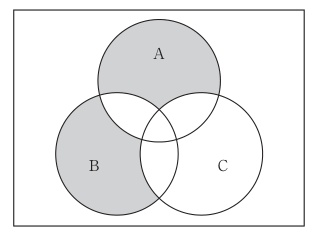
1
$A \cdot \overline{B} \cdot C + \overline{A} \cdot B \cdot C$
2
$(A \cdot B + \overline{A} \cdot \overline{B}) \cdot C$
3
$(A \cdot B + \overline{A} \cdot B) \cdot \overline{C}$
4
$(A + B) \cdot (\overline{A} + \overline{B}) \cdot \overline{C}$
5
$(A + B) \cdot (\overline{A} + \overline{B}) \cdot C$
広告
16
臨床工学技士国家試験 -
第10回 午後
類似度 53.8%
正しいのはどれか。
a
演算増幅器を用いて積分回路を作ることができる。
b
演算増幅器では反転入力端子と非反転入力端子との電位差はほぼ0である。
c
同相除去比(CMRR)を小さくするために演算増幅器による差動増幅回路を用いる。
d
入力インピーダンスを小さくするために演算増幅器による非反転増幅回路を用いる。
e
出力インピーダンスを大きくするために演算増幅器を用いる。
組み合わせ:
1. a b
2. a e
3. b c
4. c d
5. d e
35
臨床工学技士国家試験 -
第21回 午後
正答率:82%
類似度 53.6%
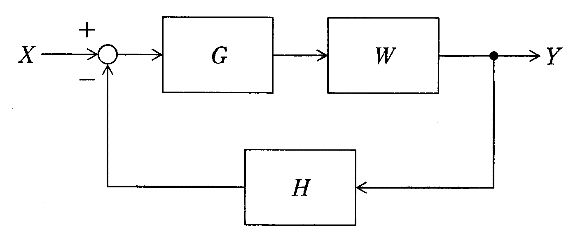
図のシステム伝達関数はどれか。
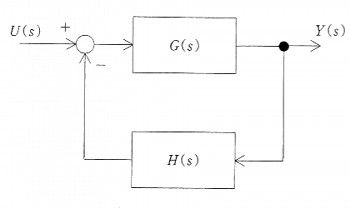
1
$\frac {1}{G\left( s\right) H\left( s\right) }$
2
$\frac {G\left( s\right) }{1-G\left( s\right) H\left( s\right) }$
3
$\frac {G\left( s\right) }{1+G\left( s\right) H\left( s\right) }$
4
$\frac {G\left( s\right) H\left( s\right) }{1-G\left( s\right) H\left( s\right) }$
5
$\frac {G\left( s\right) H\left( s\right) }{1+G\left( s\right) H\left( s\right) }$
広告