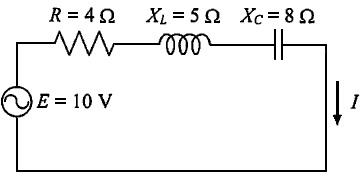臨床工学技士問題表示
臨床工学技士国家試験
検索元問題
第8回 午後 第31問
20件の類似問題
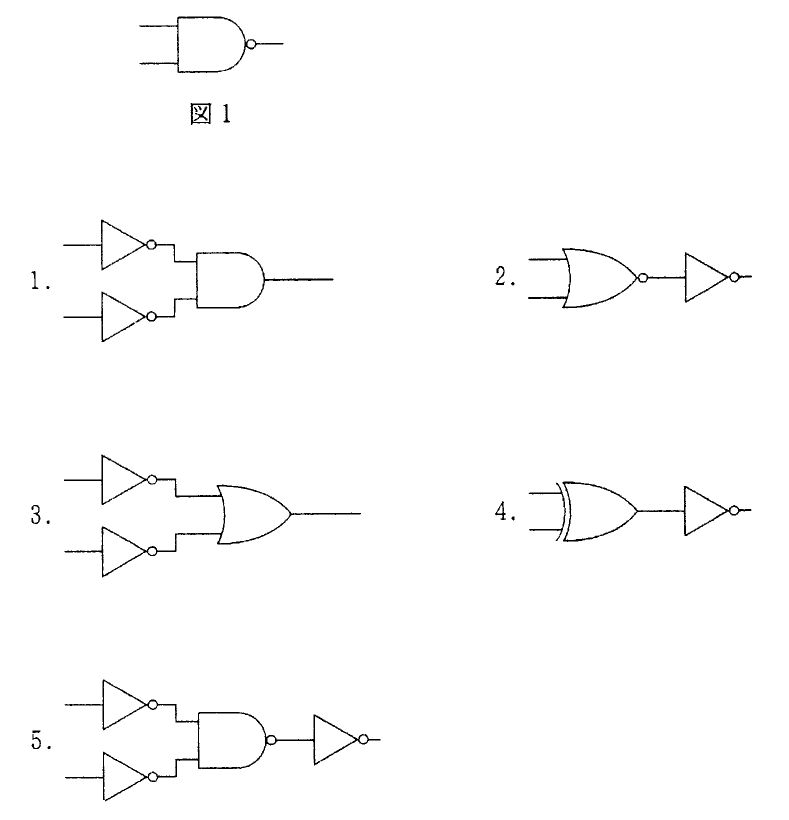
図に示す論理回路について正しいのはどれか。...
広告
7
臨床工学技士国家試験 -
第15回 午後
類似度 54.0%
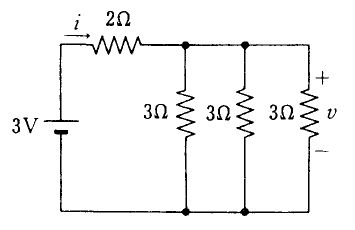
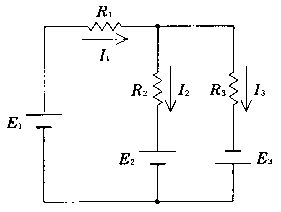
図の回路において正しい式はどれか。
a
$I_1-I_2-I_3=0$
b
$I_1+I_2+I_3=\frac{E_1}{R_1}$
c
$I_1R_1+I_3R_3=E_1-E_3$
d
$I_1R_1+I_2R_2=E_1-E_2$
e
$-I_2R_2+I_3R_3=E_2+E_3$
組み合わせ:
1. a b c
2. a b e
3. a d e
4. b c d
5. c d e
29
臨床工学技士国家試験 -
第9回 午後
正答率:57%
類似度 53.9%
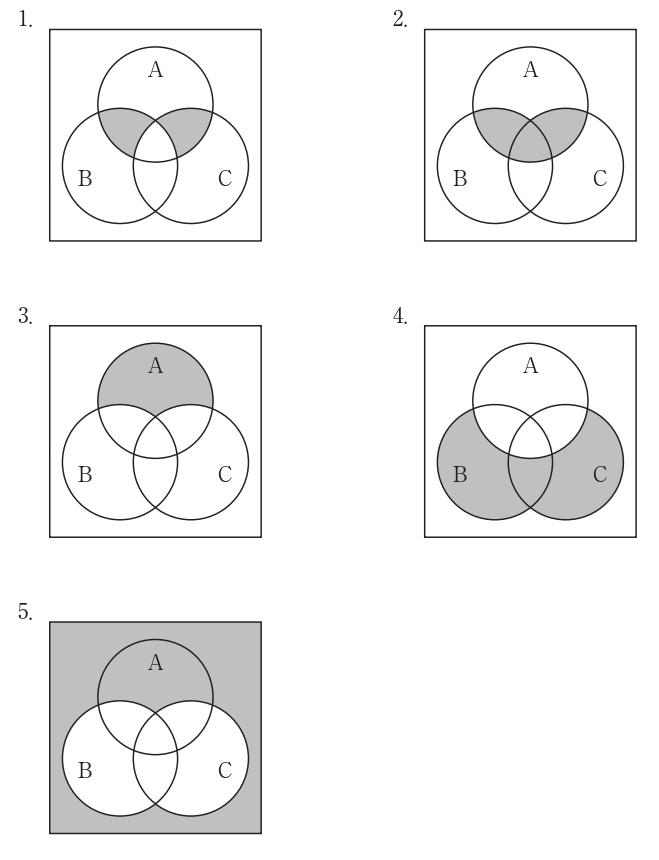
論理演算で正しいのはどれか。$\left(\overline{X+Y}\right)\bullet\left(\overline{X\bullet{Y}}\right)=$
1
$X\bullet\overline{Y}$
2
$\overline{X}\bullet{Y}$
3
$\overline{X}\bullet\overline{Y}$
4
$X\bullet{Y}$
5
$\overline{X}+\overline{Y}$
53
臨床工学技士国家試験 -
第24回 午後
正答率:51%
類似度 53.5%
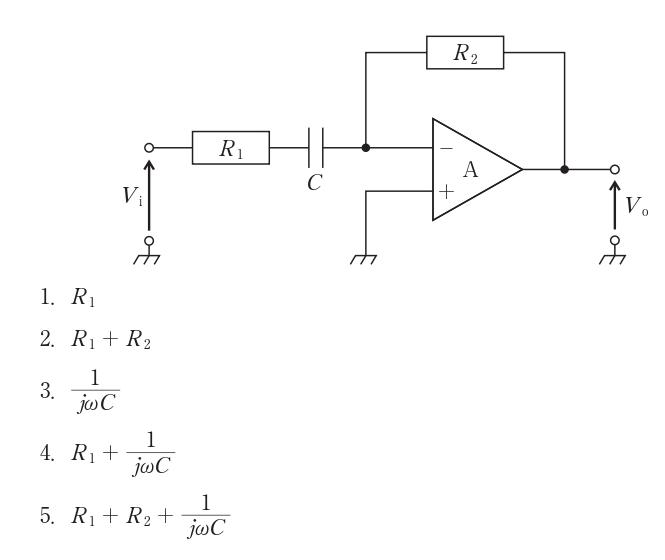
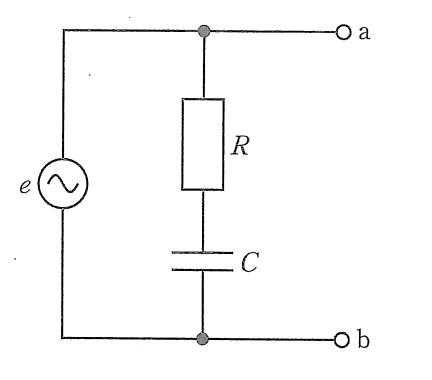
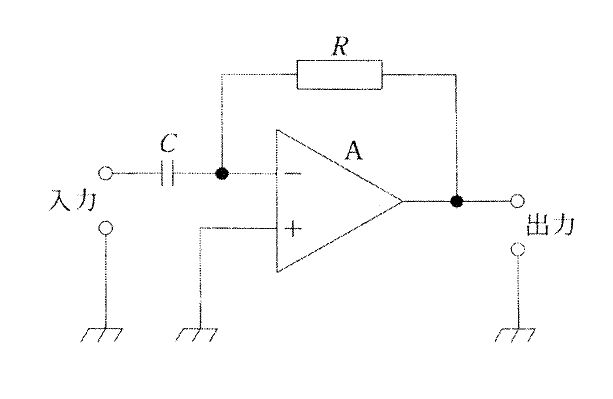
図の回路の入力インピーダンスはどれか。ただし、Aは理想演算増幅器、jは虚数単位、ωは角周波数とする。(医用電気電子工学)
1
$ j\omega C$
2
$ \frac {1}{j\omega C}$
3
$ j\omega CR$
4
$ \frac {1}{j\omega CR}$
5
$ R+\frac {1}{j\omega C}$
広告
14
臨床工学技士国家試験 -
第19回 午後
類似度 53.1%
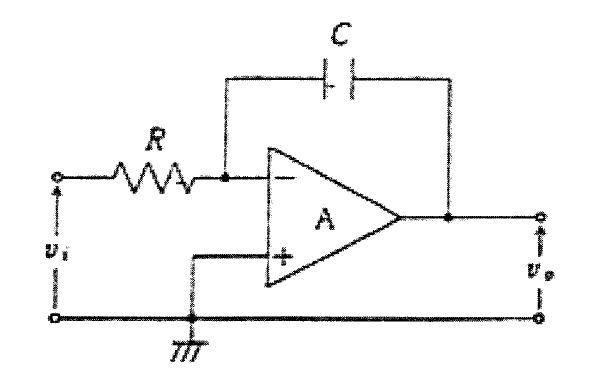
図の回路において入力Viと出力Voの関係を示す式はどれか。ただし、Aは理想増幅器とする。(電子工学)
1
$v_0=-\frac{1}{CR}\int{v_idt}$
2
$v_0=-CR\int{v_idt}$
3
$v_0=-\frac{R}{C}\int{v_idt}$
4
$v_0=-\frac{1}{CR}\frac{dv_i}{dt}$
5
$v_0=-CR\frac{dv_i}{dt}$
17
臨床工学技士国家試験 -
第18回 午後
類似度 53.1%
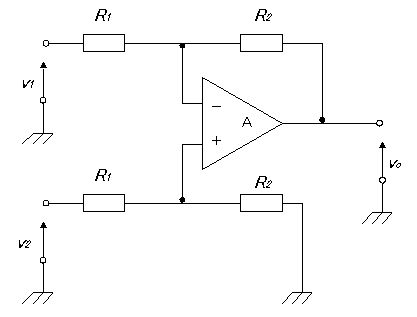
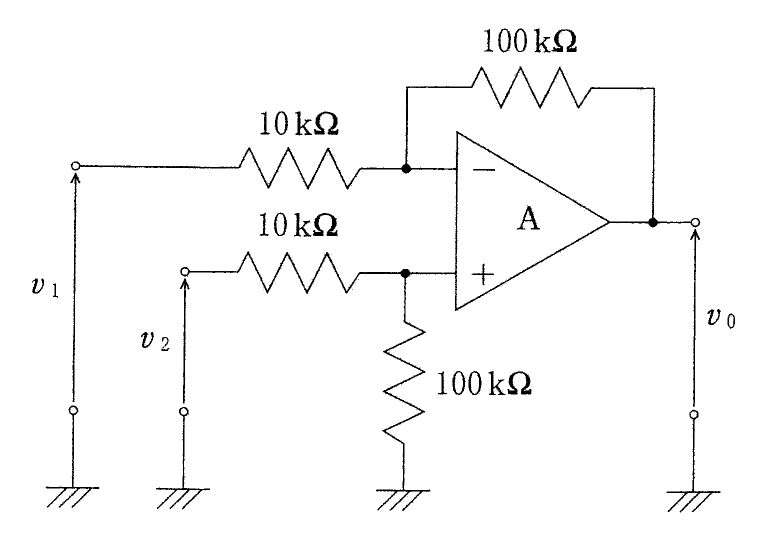
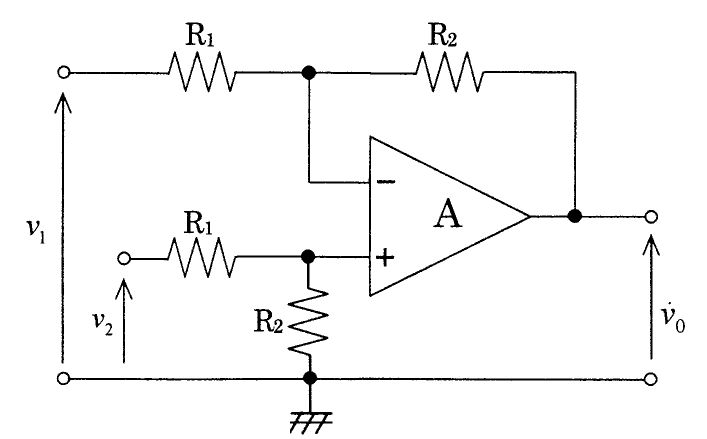
図の回路において二つの入力V1、V2とVoの関係を表す式はどれか。ただし、Aは理想演算増幅器とする。(電子工学)
1
$V_{0}=\frac {R_{1}+R_{2}}{R_{1}}\left( V_{2}-V_{1}\right) $
2
$V_{0}=\frac {R_{1}+R_{2}}{R_{2}}\left( V_{2}-V_{1}\right) $
3
$V_{0}=\frac {R_{1}+R_{2}}{R_{2}-R_{1}}\left( V_{2}-V_{1}\right) $
4
$V_{0}=\frac {R_{1}}{R_{2}}\left( V_{2}-V_{1}\right) $
5
$V_{0}=\frac {R_{2}}{R_{1}}\left( V_{2}-V_{1}\right) $
広告
55
臨床工学技士国家試験 -
第30回 午後
重要度:最重要
正答率:56%
類似度 52.4%
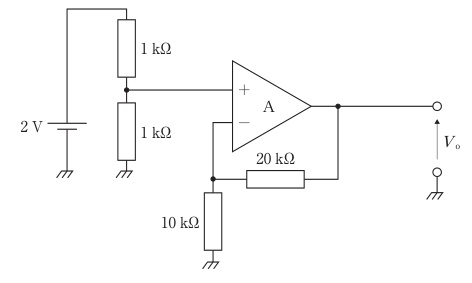
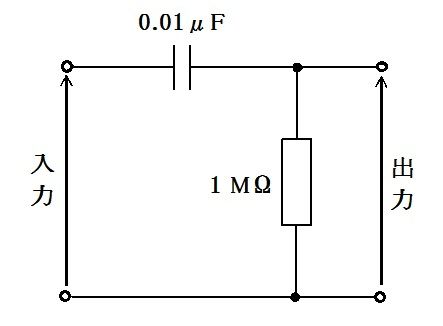
図の回路について正しいのはどれか。ただし、A は理想演算増幅器とする。
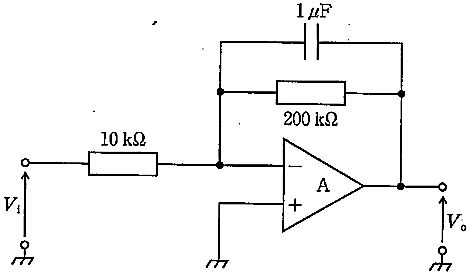
a
遮断周波数は5Hzである。
b
通過域の増幅度は20dBである。
c
遮断周波数ではViとVoの位相差はゼロである。
d
入カインピーダンスは10kΩである。
e
直流は通過域に含まれる。
組み合わせ:
1. a b
2. a e
3. b c
4. c d
5. d e
広告
53
臨床工学技士国家試験 -
第31回 午後
重要度:低
正答率:62%
類似度 52.0%
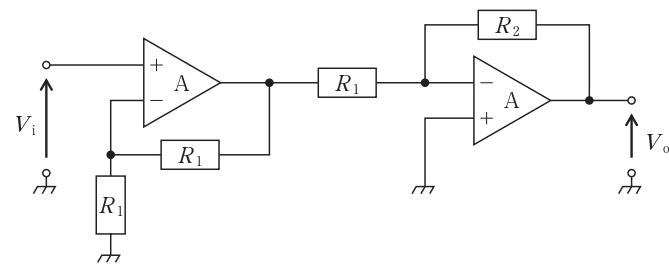
図の回路の入力電圧Viと出力電圧V。の関係式(V。/Vi)はどれか。ただし、Aは理想演算増幅器とする。
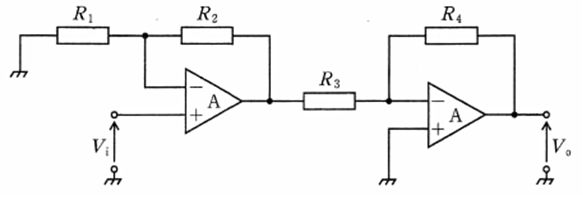
1
$ -\left( 1+\frac {R_{2}}{R_{1}}\right) \cdot \frac {R_{4}}{R_{3}}$
2
$ \left( 1+\frac {R_{2}}{R_{1}}\right) \cdot \frac {R_{4}}{R_{3}}$
3
$ -\left( 1+\frac {R_{2}}{R_{1}}\right) \cdot \left( 1+\frac {R_{4}}{R_{3}}\right) $
4
$ \frac {R_{2}}{R_{1}}\cdot \frac {R_{4}}{R_{3}}$
5
$ -\frac {R_{2}}{R_{1}}\cdot \left( 1+\frac {R_{4}}{R_{3}}\right) $
広告