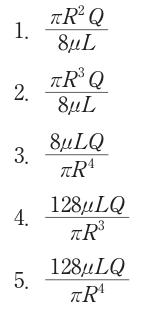第30回国試午後82問の類似問題
国試第22回午前:第82問
半径R、長さLの円管内を粘性率μの液体が流量Qで流れている。流れが定常な層流のとき、管の上流と下流の圧力差はどれか。
1:$ \frac {\pi R^{2}Q}{8\mu L}$
2:$ \frac {\pi R^{3}Q}{8\mu L}$
3:$ \frac {8\mu LQ}{\pi R^{4}}$
4:$ \frac {128\mu LQ}{\pi R^{3}}$
5:$ \frac {128\mu LQ}{\pi R^{4}}$
国試第38回午前:第82問
ある流路の内径d[m]、流路内を流れる流体の平均流速V[m/s]、密度$\rho$[kg/m³]、粘性係数$\mu$[Pa・s]、動粘性係数$\nu$[m²/s]とするとき、レイノルズ数を表す式はどれか。
a:$\frac{Vd}{\nu}$
b:$\frac{\nu}{Vd\rho}$
c:$\frac{V}{\nu\rho}$
d:$\frac{Vd}{\rho\mu}$
e:$\frac{Vd\rho}{\mu}$
1. a b 2. a e 3. b c 4. c d 5. d e