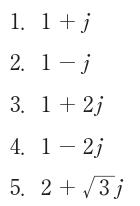第15回国試午後22問の類似問題

正しいのはどれか。ただし、jを虚数単位、Z1=1+j、Z2=1-jとする。

a: Z1Z2=2

b: Z1/Z2=-j

c: |Z2|=1

d: . Z1-Z2=2j

e: Z1の偏角=$\frac{\pi}{4}$

1. a b c　2. a b e　3. a d e　4. b c d　5. c d e

$\frac{1}{1+j}+\frac{1}{1-j}$の値はどれか。ただし、jを虚数単位($\sqrt{-1}$)とする。

1: j

2: -j

3: $\frac{1}{2}$

4: 1

5: -1

z(√3十j)の偏角がπ/2となるZはどれか。ただし、jは虚数単位である。

1: 1

2: j

3: 1十j

4: 1十j√3

5: √3十j

$ \frac {-\sqrt {3}+j}{1+j\sqrt {3}}$の偏角はどれか。ただし、j は虚数単位である。

1: $-\frac {\pi }{2}$

2: $-\frac {\pi }{6}$

3: 0

4: $\frac {\pi }{2}$

5: $\frac {\pi }{6}$

1/（√3－j）の絶対値はどれか、ただし、j は虚数単位である。

1: 1/5

2: 1/4

3: 1/3

4: 1/2

5: 1

( 1十j )(√3－j )の絶対値はどれか。ただし、jは虚数単位である。

1: 2

2: 2√2

3: 2√3

4: 2√3-2

5: 8

jを虚数単位とするとき、複素数$\frac{1}{a＋jb}$に等しいのはどれか。ただし、｜a＋jb｜＝Kとする。

1: $\frac{a}{K}-j\frac{b}{K}$

2: $\frac{a}{K}+j\frac{b}{K} $

3: $\frac{a}{K^2}-j\frac{b}{K^2}$

4: $\frac{a}{K^2}+j\frac{b}{K^2}$

5: $\frac{a^2+b^2}{K^2}-j\frac{2ab}{K^2}$

$\frac{1}{1-j\sqrt2}$の絶対値に最も近いのはどれか。ただし、は虚数単位である。

1: 0.2

2: 0.6

3: 1

4: 1.6

5: 2

(1-j)/(1+j)と等しいのはどれか。ただし、jは虚数単位である。

1: -j

2: j

3: 1-j

4: -1

5: 1

複素数√3＋jの偏角[rad]はどれか。ただし、jは虚数単位である。　(医用電気電子工学)

1: $ \frac {\pi}{6}$

2: $ \frac {\pi}{5}$

3: $ \frac {\pi}{4}$

4: $ \frac {\pi}{3}$

5: $ \frac {\pi}{2}$

複素数の偏角が - 4 /π rad となるのはどれか。 ただし、j は虚数単位である。

$\frac{1}{1-j}$の絶対値はどれか。

1: $-\frac{1}{\sqrt2}$

2: 0

3: $\frac{1}{\sqrt2}$

4: 1

5: $\sqrt2$

（ 1-j ）/（ 1+j　）と等しいのはどれか。ただし、j は虚数単位である。（電気工学）

1: -j

2: j

3: 1-j

4: -1

5: 1

1/（1+j√3）の偏角[rad]はどれか。ただし、j虚数単位である。

1: -π/3

2: -π/6

3: 0

4: π/6

5: π/3

（1＋j）・（1－j）と等しいのはどれか。ただし、jは虚数単位である。

1: 0

2: $ \sqrt2$

3: 2

4: $ \sqrt2 - j\sqrt2$

5: $ \sqrt2 + j\sqrt2$

$ j(1-j)$の偏角[rad]はどれか。ただし、は虚数単位である。

1: π

2: $\frac{\pi}{2}$

3: $\frac{\pi}{4}$

4: 0

5: $-\frac{\pi}{4}$

複素数の偏角がπ/4radとなるのはどれか。ただし、jは虚数単位である。(電気工学)

1: $1+j$

2: $1+2j$

3: $2+\sqrt3j$

4: $1-j $

5: $1-2j $

(1-j)^4と等しいのはどれか。 ただし、j は虚数単位である。

1: -4

2: -2

3: 0

4: 2

5: 4

偏角がπ/4 radとなるのはどれか。　ただし、jは虚数単位である。

1: 1+j

2: 1+2j

3: 2+√3j

4: 1-j

5: 1-2j