電磁気学の過去問

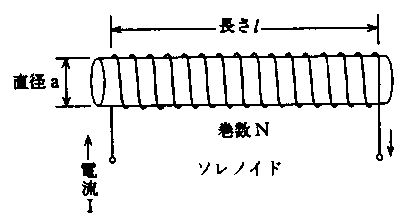
空芯ソレノイドA、B、C、Dがある。インダクタンスLの大小関係で正しいのはどれか。ただし、漏れ磁束はないものとする。

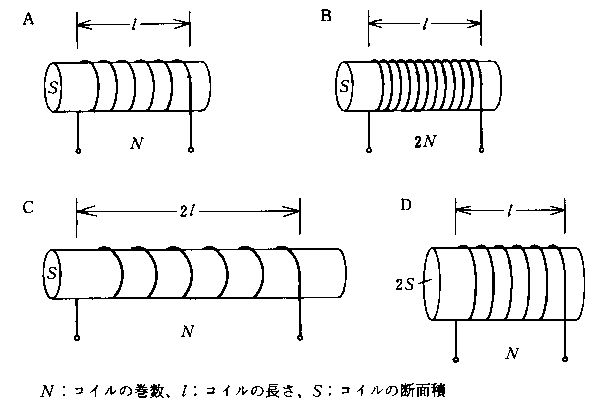
1: C>D>B>A

2: B>C>A>D

3: B>D>A>C

4: C>B>D>A

5: D>C>B>A

磁気について正しいのはどれか。

1: 磁界中の電流が受ける力の方向は磁束密度の方向に一致する。

2: 直線電流の周囲では放射状の磁界が発生する。

3: 磁界中を磁界の方向に走行する電子は力を受けない。

4: 2本の平行導線に逆向きに電流が流れていると両者の間に力は働かない。

5: 磁石は静止した陽子を引きつける。

最大容量500pFの可変コンデンサがある。容量を最大にして直流500Vの電源に接続した。その後、電源から切り離して200pFに容量を減少させた。　可変コンデンサの端子電圧は何Vになるか。　ただし、コンデンサは無損失とする。

1: 200

2: 320

3: 500

4: 790

5: 1250

正負1クーロンの点電荷の間に働く吸引力は、電荷問の距離が2cmのとき、1cmの場合に比べて何倍か。

1: 変化しない。

2: 2倍になる。

3: 1/2になる。

4: 1/4になる。

5: 1/8になる。

誤っているのはどれか。

a: 商用交流電場のシールドには銅の金網を用いる。

b: 長波帯の電磁波のシールドには電磁波吸収材を用いる。

c: 静電場のシールドには導電率の低い材料を厚い層にして用いる。

d: 静磁場のシールドには透磁率の高い金属を厚い層にして用いる。

e: 変動磁場のシールドには導電率の高い金属と透磁率の高い金属を交互に組合せて用いる。

1. a b　2. a e　3. b c　4. c d　5. d e

正しいのはどれか。

a: 導線に電流を流したとき、その周りの磁界には影響を及ぼさない。

b: 平行な2本の導線に逆方向の電流が流れると導線間には反発力が生じる。

c: 発電機では磁界中で導体を動かすことにより起電力を発生させている。

d: 棒磁石を直線電流と平行に置いたとき、棒磁石は力を受けない。

e: 電子が直線電流の近くを同方向に走行していると直線電流に向かう力を受ける。

1. a b　2. a e　3. b c　4. c d　5. d e

強磁性体について正しいのはどれか。

a: 強磁性体に磁石を近づけると引力が働く。

b: 永久磁石は強磁性体の保磁力の性質を利用したものである。

c: コバルトは強磁性体である。

d: 強磁性体はいくら加熱しても磁性体の性質を失わない。

e: 強磁性体の比透磁率はほぼ1である。

1. a b c　2. a b e　3. a d e　4. b c d　5. c d e

全く帯電していない完全導体を一様な電界の中に置いた。正しいのはどれか。

a: 電気力線は導体を置く前と置いた後では異なる。

b: 導体の表面には電磁誘導によって負の電荷が現れる。

c: 導体表面の電位は一様ではない。

d: 導体の内部に静電誘導によって負の電荷が現れる。

e: 導体の電荷の総和は0に保たれる。

1. a b　2. a e　3. b c　4. c d　5. d e

図のように一様磁界中でコイルが回転し、コイル端子が外部と接続可能となっている装置がある。正しいのはどれか。

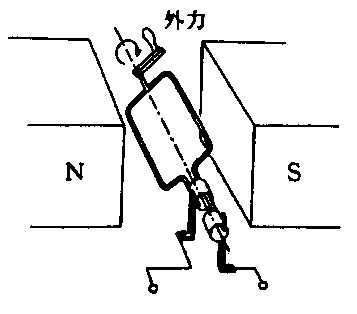
a: 外力によってコイルを連続回転させると、端子間に直流電圧が発生する。

b: 外力によってコイルを連続回転させると、端子間に交流電圧が発生する。

c: 外力を加えないで端子Fに電池を接続すると、コイル面が磁界と垂直になって静止する。

d: 外力を加えないで端子間に電池を接続すると、コイル面が磁界と平行になって静止する。

e: 外力を加えないで端子間に電池を接続すると、コイルが連続回転する。

1. a b　2. a e　3. b c　4. c d　5. d e

シールドについて正しいのはどれか。

1: 磁力線を遮断するに誘電体が適している。

2: 真空は電気力線を遮断する。

3: 静電界をシールドするには誘電率の小さい材料が適している。

4: 電波をシールドするには導電率の大きい材料が適している。

5: 透磁率の小さい材料は磁気シールドに適している。

図に示すソレノイド（a≪l）について正しいのはどれか。

a: 内部の磁界の強さは長さlに反比例する。

b: 電流Iを2倍にすると磁界の強さは4倍になる。

c: 直径aを2倍にすると磁界の強さは2倍になる。

d: 内部はほぼ均一磁界である。

e: 同じ長さで巻数Nを2倍にすると磁束密度は2倍になる。

1. a b c　2. a b e　3. a d e　4. b c d　5. c d e

正しいのはどれか。

a: 直線電流の周りには電流が時間的変化をするときだけ磁力線が生じる。

b: 円形コイルに電流を流すとコイル面内ではコイル面と垂直方向に磁界が発生する。

c: 直線電流がつくる磁界の大きさは距離に反比例する。

d: 磁界中で運動する電荷は運動速度に反比例する力を受ける。

e: 2本の平行導線に同方向に電流が流れていると両者の間に反発力が働く。

1. a b　2. a e　3. b c　4. c d　5. d e

1μFの平行平板コンデンサについて正しいのはどれか。

1: 極板面積を2倍にすると容量が4μFになる。

2: 極板間距離を2倍にすると容量が2μFになる。

3: 100V、50Hzの交流電源に接続すると約3.1mAの電流が流れる。

4: 正弦波交流電圧をかけると、流れる電流の位相は電圧に対して90°進む。

5: 正弦波交流電圧をかけて、周波数を2倍にすると流れる電流は4倍になる。

図のように誘電体を挟んだ平行平板導体に電圧を加えた。正しいのはどれか。

a: 平行導体板間の静電容量は100μFである。

b: 誘電体中に分極が生じる。

c: 誘電体を取り除くと静電容量は1/5になる。

d: 誘電体中の電界の強さは1000V/mである。

e: 誘電体を取り除いたときの電界の強さは500V/mである。

1. a b c　2. a b e　3. a d e　4. b c d　5. c d e

図のように正方形の頂点A、B、C、Dに電荷$Q_A$、$Q_B$、$Q_C$、$Q_D$がある。正しいのはどれか。

1: $Q_A$は対角線ACの方向に力を受ける。

2: $Q_A$の受ける力は零である。

3: $Q_B$は辺BCの方向に力を受ける。

4: $Q_B$の受ける力は零である。

5: $Q_A$の受ける力の方向と$Q_B$の受ける力の方向とは同じである。

正しいのはどれか。

a: 電荷に働く力はその場所の電界の2乗に比例する。

b: 電界とはその場所に置かれた電子の受ける力をいう。

c: 電界の単位はV/mである。

d: 1Cの電荷を移動させるのに1Jのエネルギーが必要であるとき、その電位差を1Vという。

e: 電気力線は等電位面と常に平行である。

1. a b　2. a e　3. b c　4. c d　5. d e

シールド（遮蔽）について正しいのはどれか。

1: 磁力線は抵抗体に囲まれた領域内は入り込まない。

2: 磁率が小さい材料ほど磁気シールド効果が大きい。

3: 時間的変化が遅い電界のシールドには導電率の小さい材料が適している。

4: 波長の短い電波にシールドには誘電率が小さい材料が適している。

5: 周波数の低い電波にシールドには導電率の大きい材料が適している。

図に示すインダクタ（コイル）に電流Iを流すとき正しいのはどれか。

1: 電流Iを2倍にすると磁心中の磁束は4倍になる。

2: 電流Iに逆比例した逆起電力が発生する。

3: 磁心中の磁束の時間的変化率に比例した逆起電力が発生する。

4: 巻数Nを2倍にするとインダクタンスは2倍になる。

5: 磁心の透磁率が大きいほどインダクタンスは小さい。

磁気について正しいのはどれか。

a: 直流電流の周りにはこれを中心とする同心円上に磁力線が生じる。

b: 円形コイルに電流を流すとコイル面内では同心円上に磁界が発生する。

c: 直流電流によって生じる磁束密度の大きさは距離の2乗に反比例する。

d: 2本の平行導線に同方向に電流が流れていると両者の間に反発力が働く。

e: 磁束密度が磁気誘導によって著しく増加するものを強磁性体という。

1. a b　2. a e　3. b c　4. c d　5. d e

正しいのはどれか。

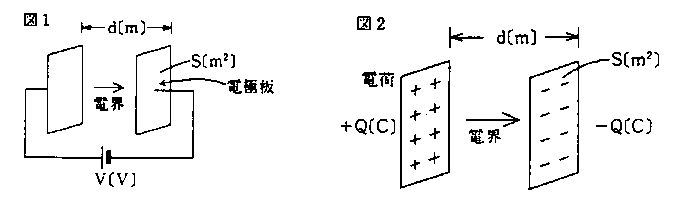
a: 図1に示す電極板間の電界の強さは$\frac{V}{S}$である。

b: 図2に示す電極板間の電界の強さは$\frac{Qd}{S}$である。

c: 図1に示す電極板間に比誘電率εrの誘電体を狭むと電界の強さは$\frac{1}{\varepsilon_r}$となる。

d: 図2に示す電極板間に比誘電率εrの誘電体を狭むと電界の強さは$\frac{1}{\varepsilon_r}$となる。

e: 図1の電極板の間隔を$\frac{d}{2}$にすると電界の強さは2倍になる。

1. a b　2. a e　3. b c　4. c d　5. d e