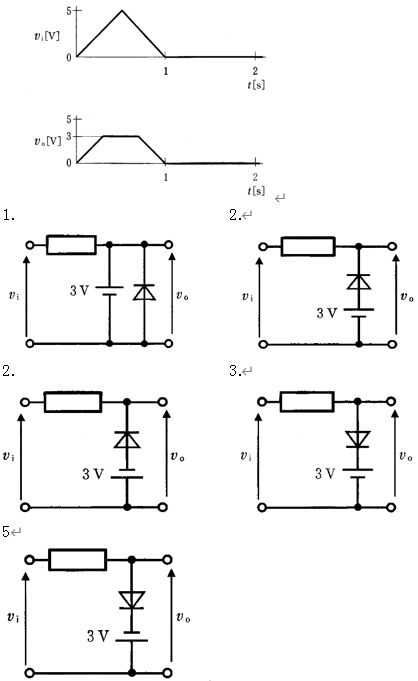
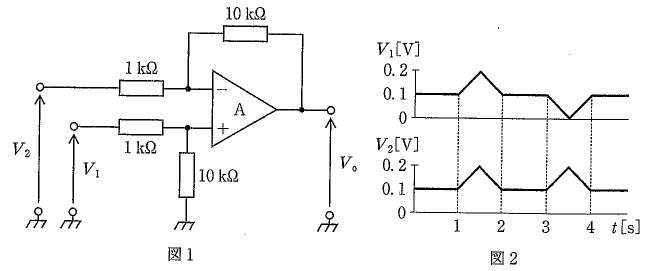
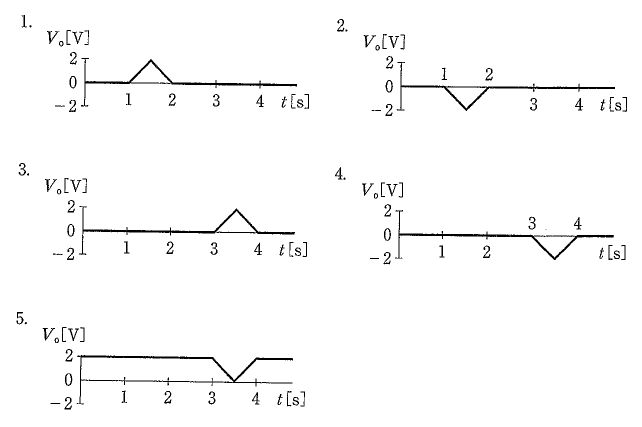
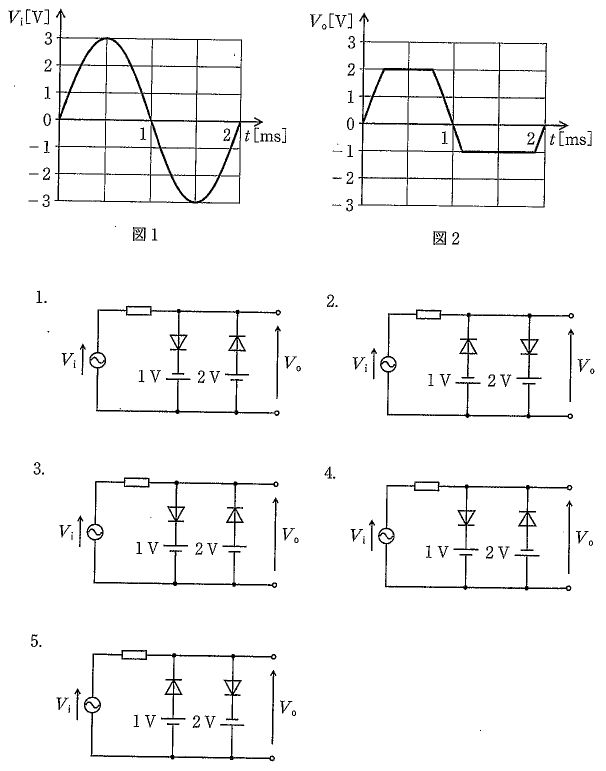
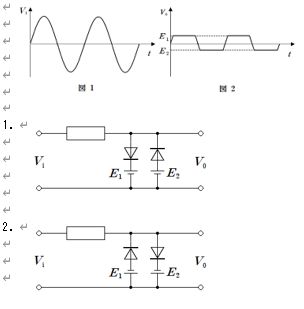
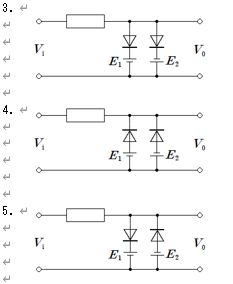
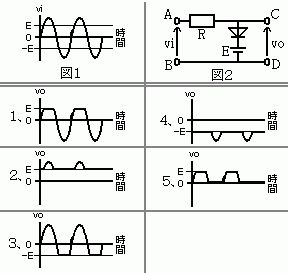
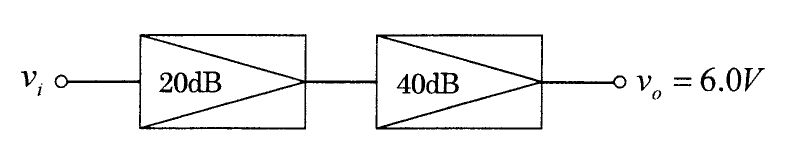
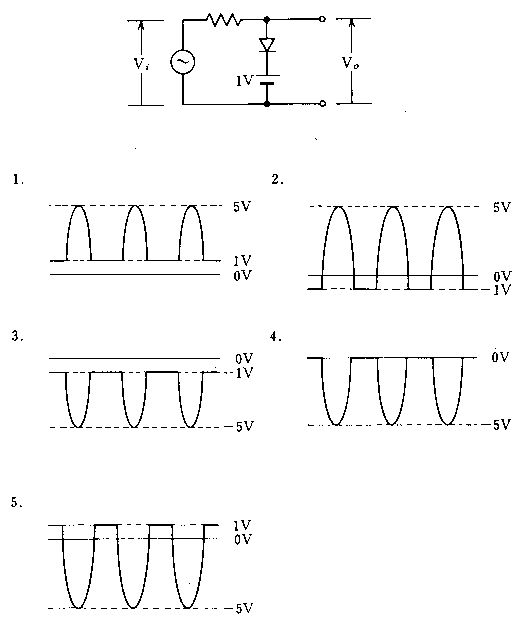
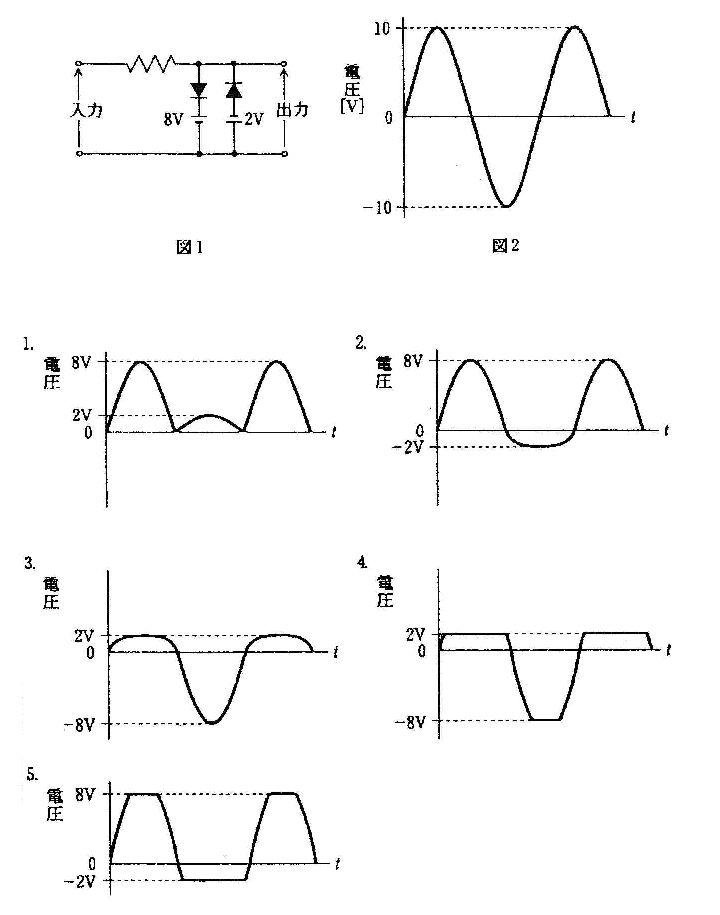
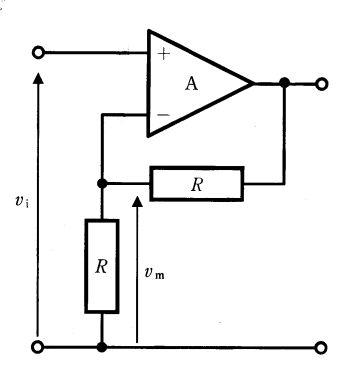
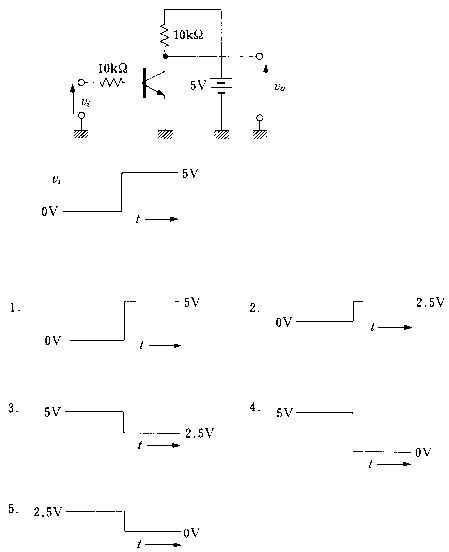
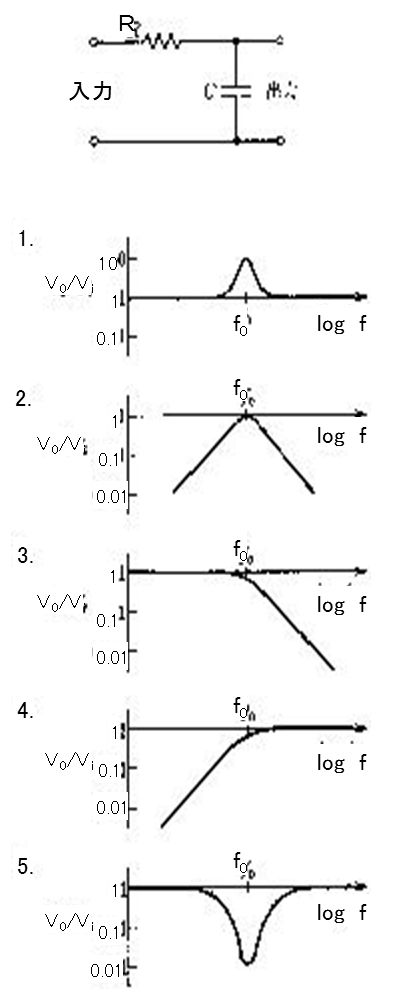
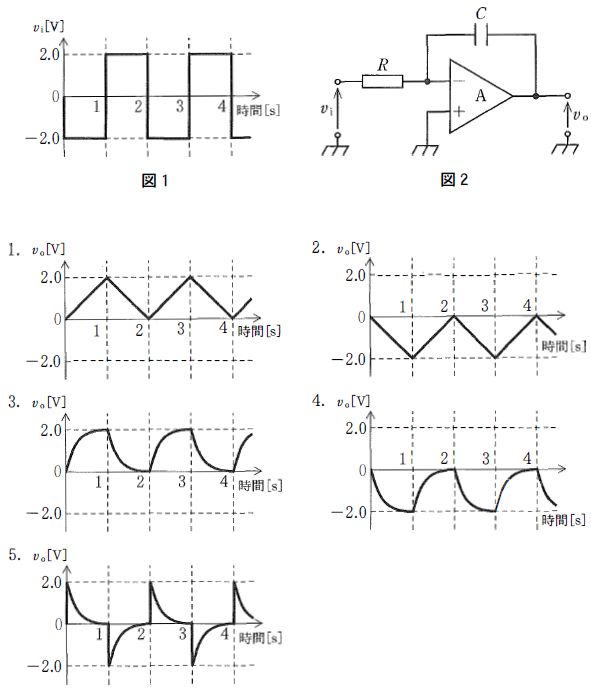
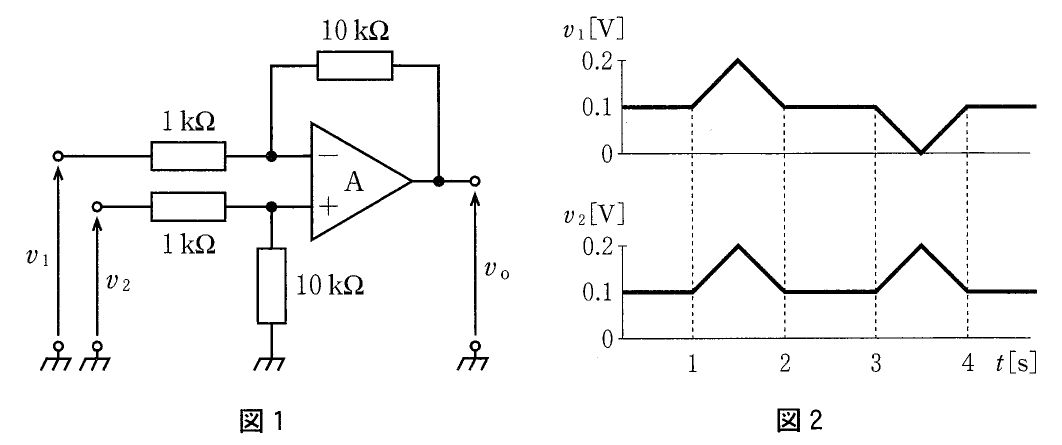
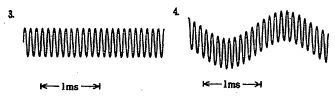
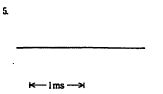
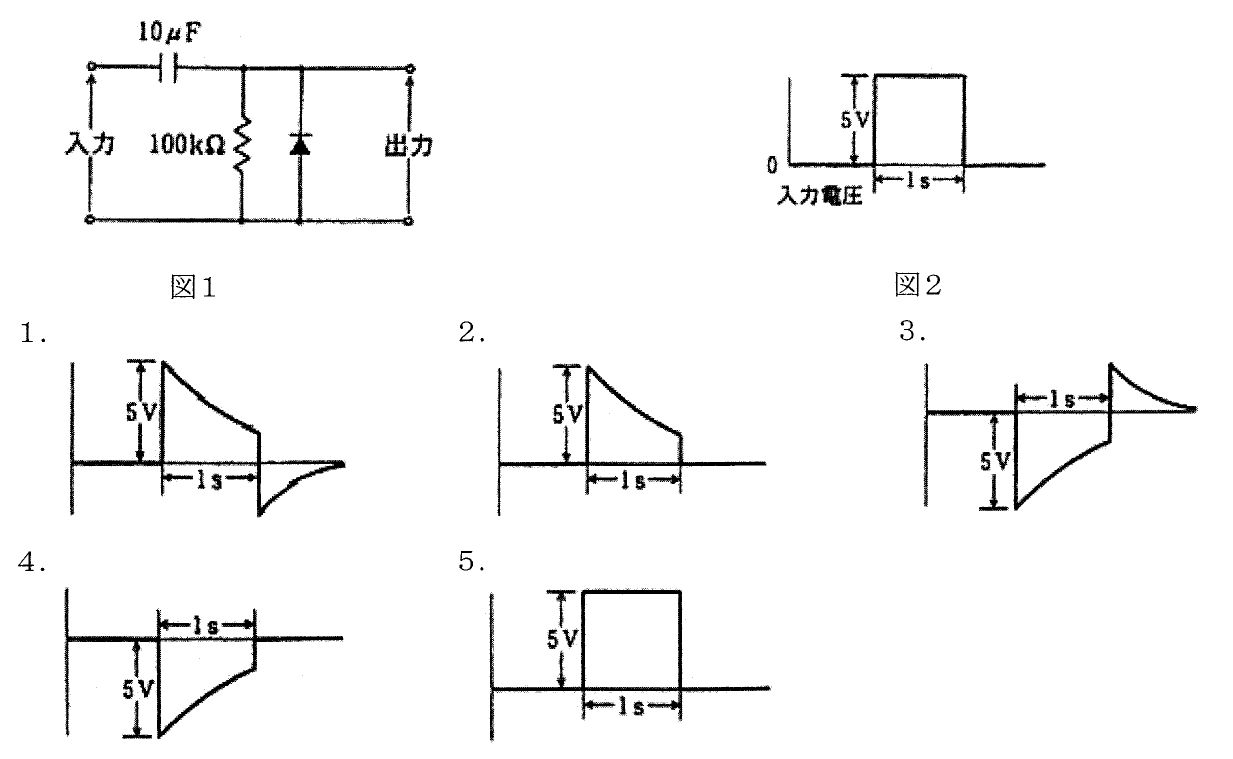
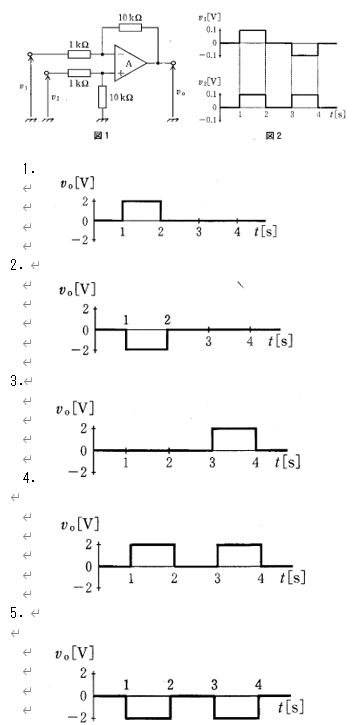
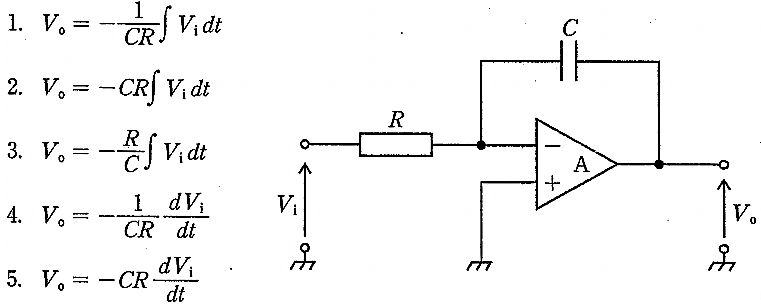
第3回国試午後23問の類似問題
国試第31回午後:第53問
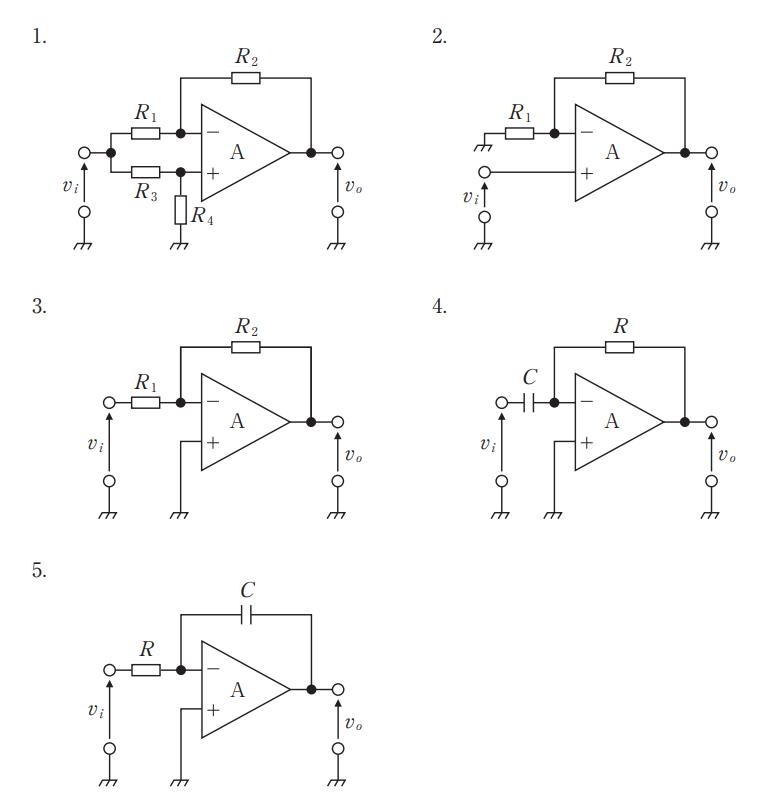
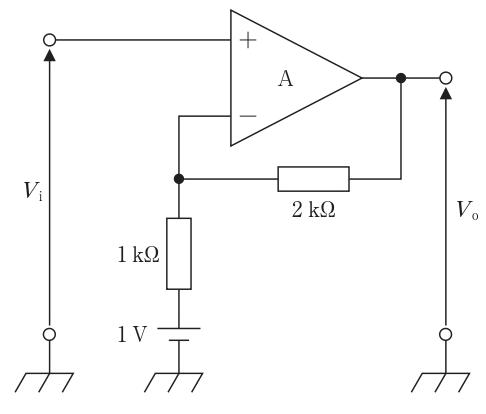
図の回路の入力電圧Viと出力電圧V。の関係式(V。/Vi)はどれか。ただし、Aは理想演算増幅器とする。
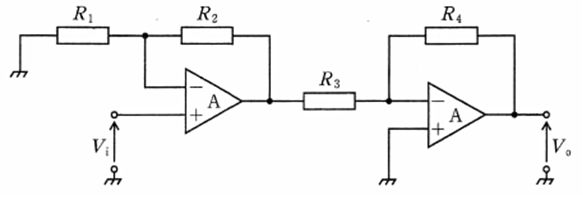
1: $ -\left( 1+\frac {R_{2}}{R_{1}}\right) \cdot \frac {R_{4}}{R_{3}}$
2: $ \left( 1+\frac {R_{2}}{R_{1}}\right) \cdot \frac {R_{4}}{R_{3}}$
3: $ -\left( 1+\frac {R_{2}}{R_{1}}\right) \cdot \left( 1+\frac {R_{4}}{R_{3}}\right) $
4: $ \frac {R_{2}}{R_{1}}\cdot \frac {R_{4}}{R_{3}}$
5: $ -\frac {R_{2}}{R_{1}}\cdot \left( 1+\frac {R_{4}}{R_{3}}\right) $