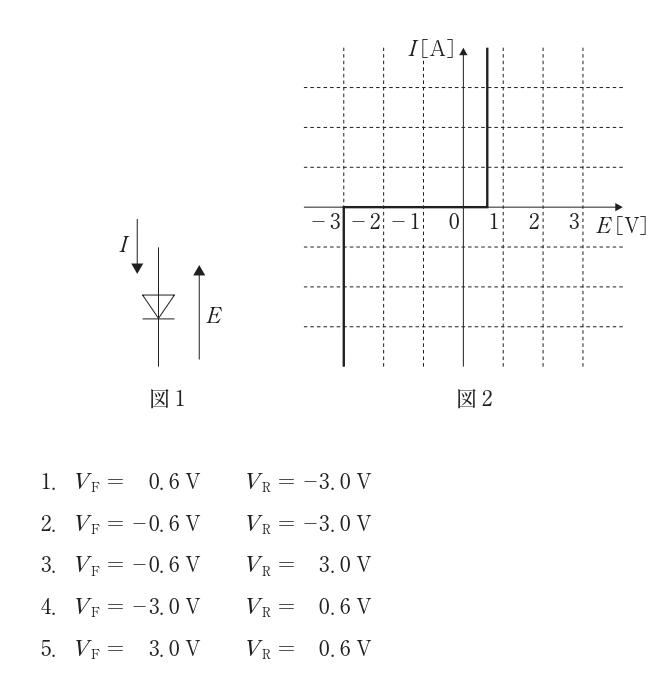
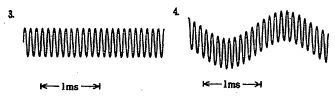
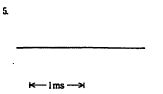
第9回国試午後14問の類似問題
国試第31回午後:第53問
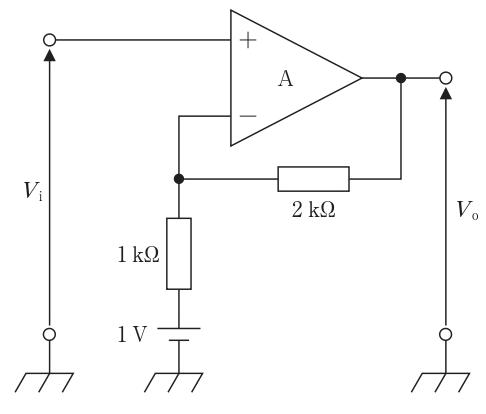
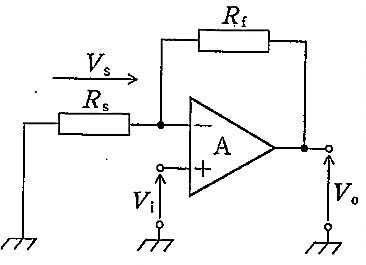
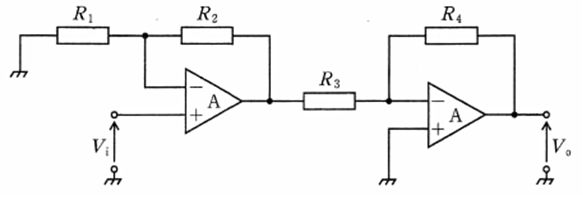
図の回路の入力電圧Viと出力電圧V。の関係式(V。/Vi)はどれか。ただし、Aは理想演算増幅器とする。
1: $ -\left( 1+\frac {R_{2}}{R_{1}}\right) \cdot \frac {R_{4}}{R_{3}}$
2: $ \left( 1+\frac {R_{2}}{R_{1}}\right) \cdot \frac {R_{4}}{R_{3}}$
3: $ -\left( 1+\frac {R_{2}}{R_{1}}\right) \cdot \left( 1+\frac {R_{4}}{R_{3}}\right) $
4: $ \frac {R_{2}}{R_{1}}\cdot \frac {R_{4}}{R_{3}}$
5: $ -\frac {R_{2}}{R_{1}}\cdot \left( 1+\frac {R_{4}}{R_{3}}\right) $
国試第21回午後:第17問
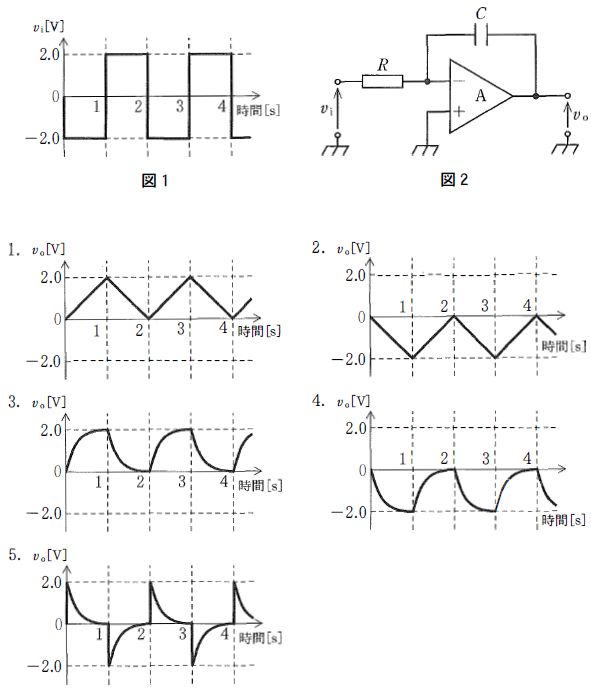
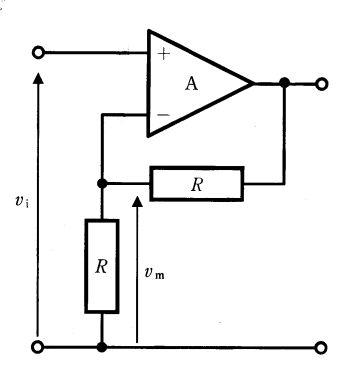
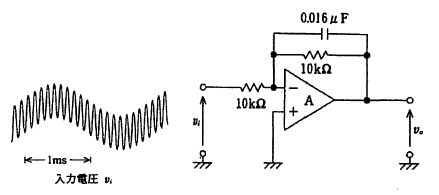
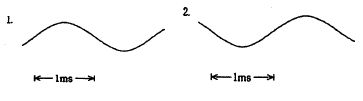
図の回路に、周波数fの正弦波電圧viを入力した。出力電圧voについて正しいのはどれか。ただし、Aは理想演算増幅器、fo = 1 / 2πCfRf とする。
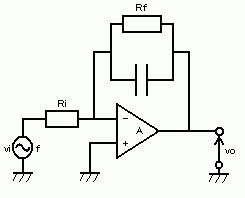
a: fがfoより十分小さければ vo = -(Rf/Ri) vi となる。
b: fがfoより十分大きければ vo = -(Rf/Ri)vi となる。
c: f = fo でvoの振幅は最大となる。
d: fがfoより十分小さければvoの振幅は0に近づく。
e: fがfoより十分大きければvoの振幅は0に近づく。
1. a b 2. a e 3. b c 4. c d 5. d e
国試第23回午後:第48問
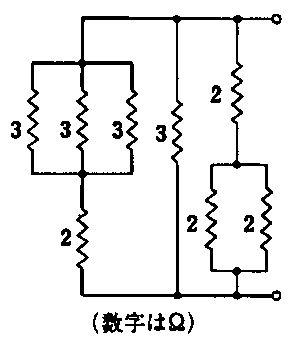
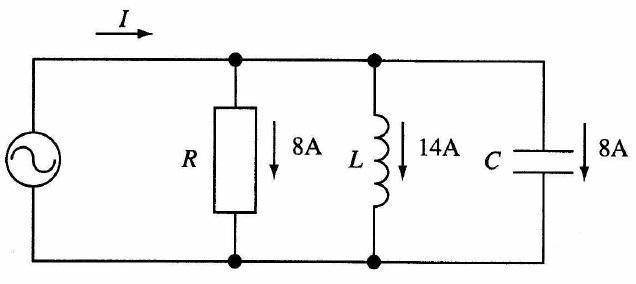
図のRC並列回路のインピーダンスの大きさはどれか。ただし、ωは角周波数である。
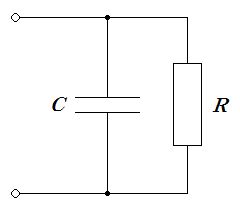
1: $\frac{R}{\sqrt{1+\omega^2C^2R^2}}$
2: $ R\sqrt{1+\omega^2C^2R^2}$
3: $\frac{1}{\omega C\sqrt{1+\omega^2C^2R^2}}$
4: $\frac{\sqrt{1+\omega^2C^2R^2}}{\omega C}$
5: $\frac{R}{\omega C}\sqrt{1+\omega^2C^2R^2}$