Loading...

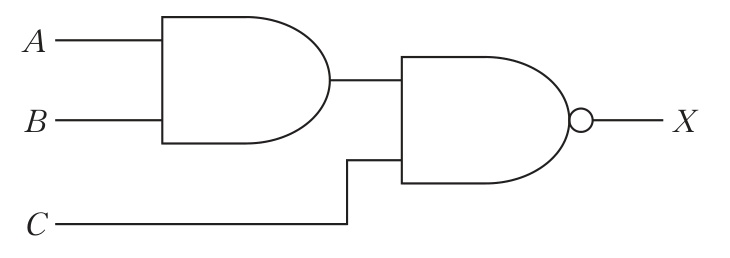
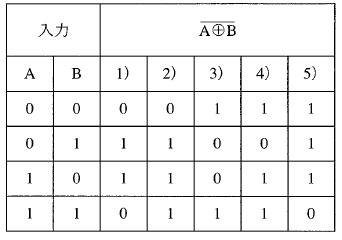
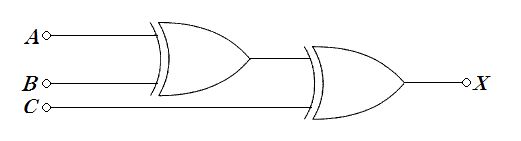
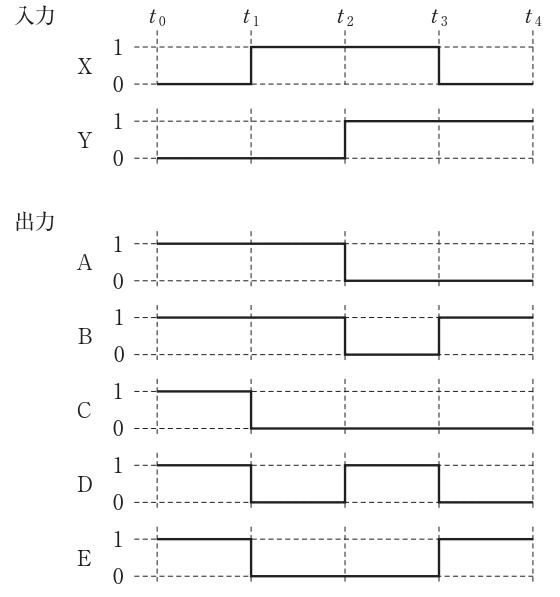
第33回ME2午前35問の類似問題

国試第38回午前：第57問

論理式$A + (B \cdot C)$に等しいのはどれか。

1:$A \cdot (B + C)$
2:$(A + B) \cdot (A + C)$
3:$(A \cdot B) + (A \cdot C)$
4:$A \cdot (\overline{B} \cdot \overline{C}) + (B \cdot C)$
5:$\overline{A} + (B \cdot C)$

国試第13回午後：第23問

論理式$\overline{A+\overline{B}}$に等しいのはどれか。

1:$ A\cdot\overline{B}$
2:$\overline{A}\cdot B$
3:$\overline{A}\cdot\overline{B}$
4:$\overline{A}+B$
5:$ A+\overline{B}$

国試第8回午後：第30問

論理式$\overline{\overline{A}+B}$に等しいのはどれか。

1:$A\cdot \overline {B}$
2:$\overline {A}\cdot B$
3:$\overline {A}\cdot \overline {B}$
4:$\overline {A}+B$
5:$A+\overline {B}$

国試第23回午後：第58問

論理演算$\overline {\left( A+B\right) }\cdot \left( \overline {A}+B\right) $に等しいのはどれか。

1:$\overline{A}$
2:$\overline{B}$
3:$\overline {A}\cdot B$
4:$A\cdot \overline {B}$
5:$\overline {A}\cdot \overline {B}$

国試第33回午前：第61問

論理式 $A_{B}\left( \overline{B+C}\right)$ を表すベン図はどれか。 ただし、図中の網掛け部分が論理値の 1 を表す。

33-AM-61

ME2第28回午前：第31問

次の論理式で誤っているのはどれか。ただし、A＋BはAとBの論理和、A・BはAとBの論理積、ĀはAの論理否定を表す。

img11202-31-0
1:1
2:2
3:3
4:4
5:5

国試第25回午前：第60問

論理式において、$ AB+A\overline {B}=1$となる条件はどれか。

1:A = 1
2:B = 1
3:A、Bによらない
4:A = 0、B = 1
5:A = 0、B = 0

国試第14回午後：第21問

論理式において$ \mathrm{AB}+\overline{\mathrm{AB}}=1$となる条件はどれか。

1:A=1
2:B=1
3:A、Bによらない
4:A=0、B=1
5:A=0、B=0

国試第19回午後：第35問

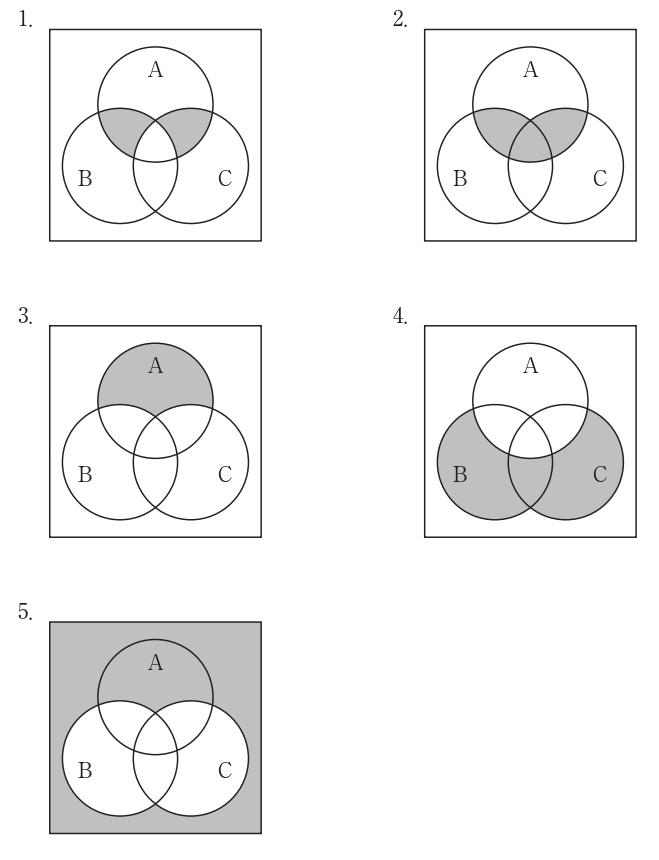
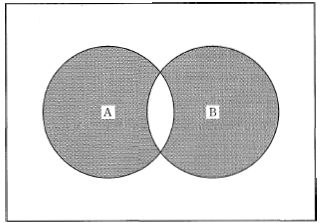
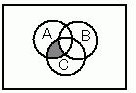
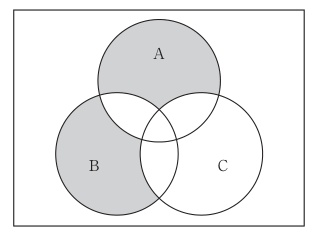
円で表される集合A，B，Cがある。網掛け部分に対応する論理式はどれか。（情報処理工学）

19PM35-0
1:$\left(A+B\right)\bullet\overline{C}$
2:$ B\bullet\left(A+C\right)$
3:$ A\bullet{B}+B\bullet{C}$
4:$\overline{\left(A+B\right)}\bullet{C}$
5:$ B\bullet\overline{\left(A+C\right)}$

国試第31回午前：第62問

論理式 X＝A･B+A･Cと等価な論理回路はどれか。

31AM62-0

国試第37回午後：第55問

図の回路と等価な論理式はどれか。

137055
1:$X = A \cdot B + C$
2:$X = A \cdot B + \overline{C}$
3:$X = (\overline{A} + \overline{B}) \cdot C$
4:$X = (A + B) \cdot C$
5:$X = (A + B) \cdot \overline{C}$

国試第20回午後：第29問

次の論理式を簡単化したものはどれか。$ X=\left(A+B\right)\bullet\left(\overline{A}+B\right)$（情報処理工学）

1:1
2:A
3:B
4:A・B
5:$\overline{A}\bullet\overline{B}$

国試第37回午前：第59問

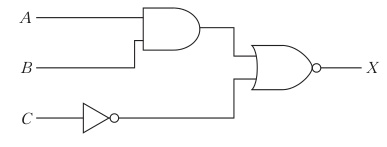
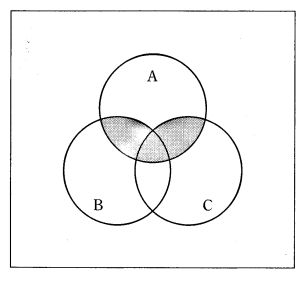
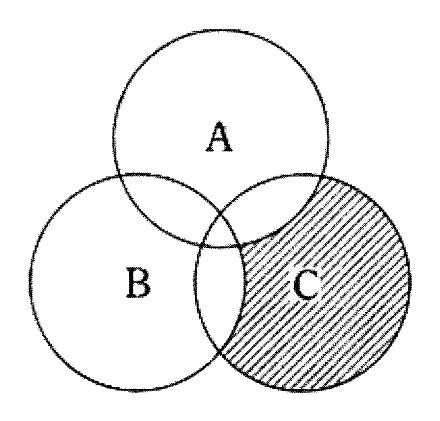
図の網掛け部分を表す論理式はどれか。

137159
1:$A \cdot \overline{B} \cdot C + \overline{A} \cdot B \cdot C$
2:$(A \cdot B + \overline{A} \cdot \overline{B}) \cdot C$
3:$(A \cdot B + \overline{A} \cdot B) \cdot \overline{C}$
4:$(A + B) \cdot (\overline{A} + \overline{B}) \cdot \overline{C}$
5:$(A + B) \cdot (\overline{A} + \overline{B}) \cdot C$

国試第38回午後：第55問

図の回路の論理式はどれか。

xozPfe80n_
1:$X = A + B \cdot \overline{C}$
2:$X = A + B + C$
3:$X = \overline{A} \cdot \overline{B} \cdot \overline{C}$
4:$X = A \cdot B \cdot \overline{C}$
5:$X = \overline{A \cdot B \cdot C}$

国試第26回午前：第59問

円で表される集合A、B、Cがある。図の網かけ部分に対応する論理式はどれか。

26AM59-0
1:A・(B + C)
2:B・(A + C)
3:A + B・C
4:B + A・C
5:C + A・B

国試第28回午前：第62問

集合A、Bの論理演算で図の網掛け部分を表すのはどれか。

28AM62-0
1:AND
2:OR
3:NOT
4:XOR
5:NOR

ME2第39回午前：第35問

論理式A⊕Bの真理値表として正しいのはどれか。 ただし、1を真とする。

img39781-35-0

国試第23回午後：第53問

排他的論理和(exclusive OR)2素子からなる図の回路の出力Xが1になるのはどれか。

23PM53-0
1:A=0、 B=0、 C=0
2:A=0、 B=0、C=1
3:A=1、B=1、 C=0
4:A=1、B=0、 C=1
5:A=1、B=1、 C=1

国試第21回午後：第33問

円で表される集合A、B、Cがある。図の網掛け部分に対応する論理式はどれか。

21PM33-0
1:$A\cdot \overline {B}\cdot C$
2:$A\cdot B\cdot C$
3:$A+\overline {B}\cdot C$
4:$A\cdot B+C$
5:$\overline {\left( A+B\right) }\cdot C$

国試第34回午後：第60問

論理演算 $\overline{X\cdot Y}$を求める論理回路がある。図のような X、Y を入力した時の出力はどれか。

34-PM-60
1:A
2:B
3:C
4:D
5:E