臨床工学技士問題表示
臨床工学技士国家試験
検索元問題
第23回 午後 第53問
20件の類似問題
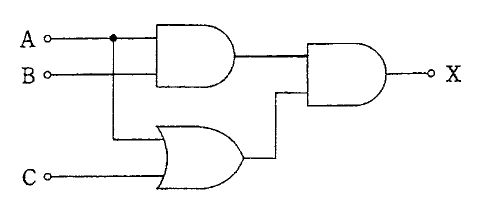
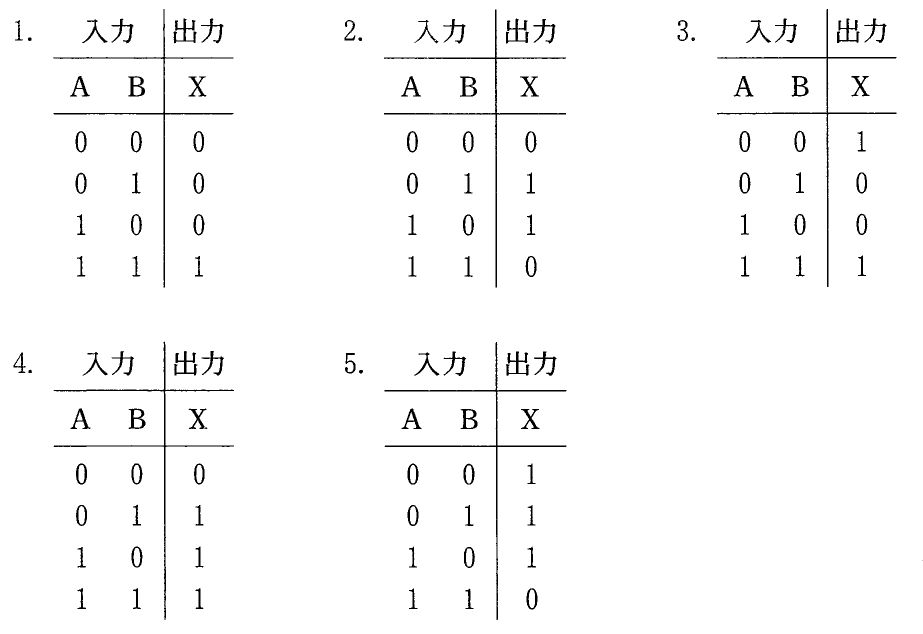
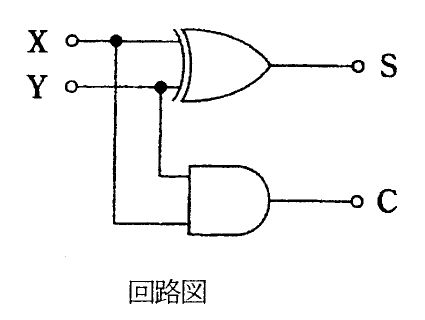
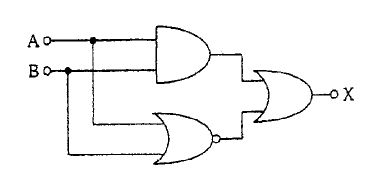
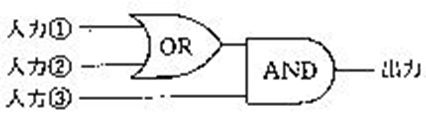
排他的論理和(exclusive OR)2素子からなる図の回路の出力Xが1になるのはどれか。...
広告
55
臨床工学技士国家試験 -
第38回 午後
類似度 76.7%
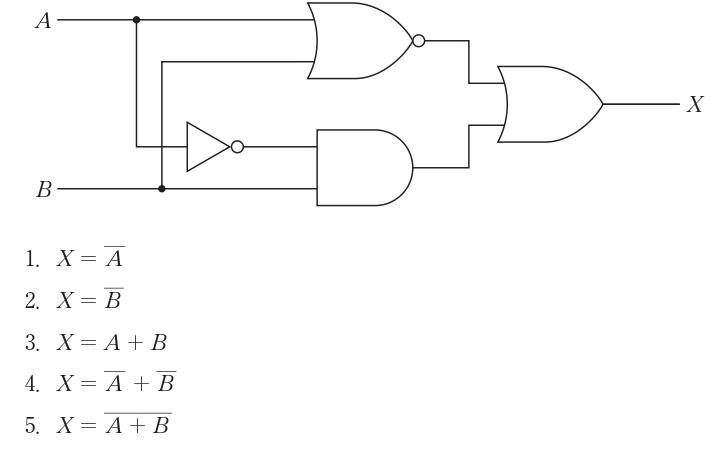
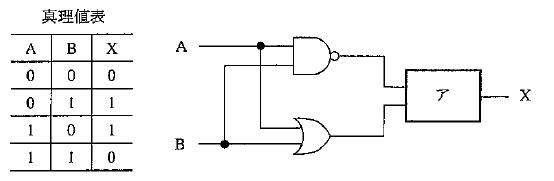
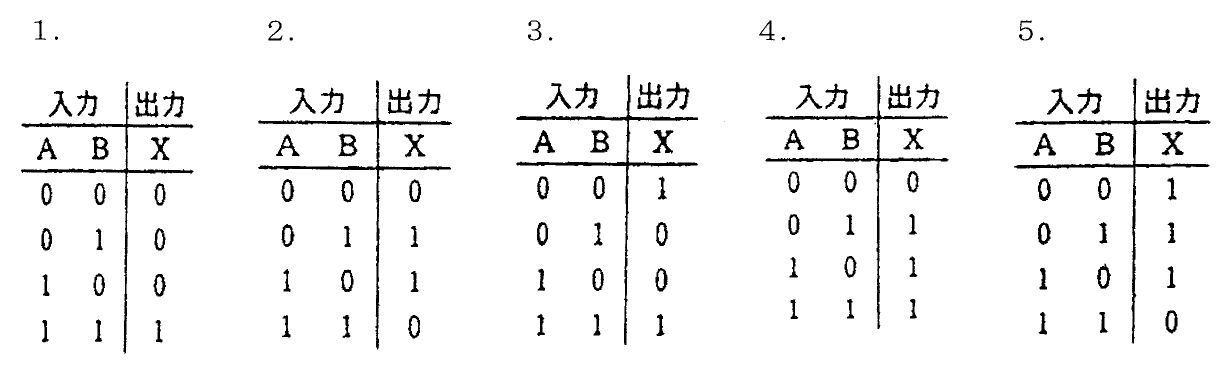
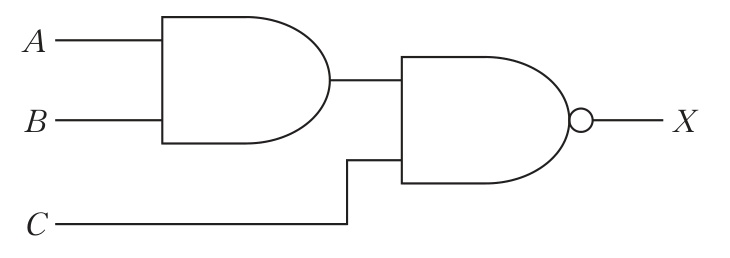
図の回路の論理式はどれか。
1
$X = A + B \cdot \overline{C}$
2
$X = A + B + C$
3
$X = \overline{A} \cdot \overline{B} \cdot \overline{C}$
4
$X = A \cdot B \cdot \overline{C}$
5
$X = \overline{A \cdot B \cdot C}$
20
臨床工学技士国家試験 -
第14回 午後
類似度 76.5%
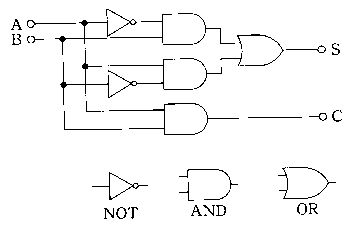
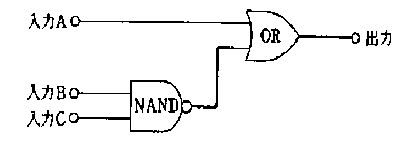
図の論理回路について誤っているのはどれか。
a
入力Aが1のとき、出力は他の入力に無関係に1である。
b
入力Bが0のとき、出力は他の入力に無関係に1である。
c
入力Aが0、入力Bが1のとき、出力は入力Cに無関係に1である。
d
入力B、入力Cが1のとき、出力は入力Aに無関係に0である。
e
入力A、入力B、入力Cが0のとき、出力は1である。
組み合わせ:
1. a b
2. a e
3. b c
4. c d
5. d e
広告
60
臨床工学技士国家試験 -
第22回 午後
類似度 76.3%
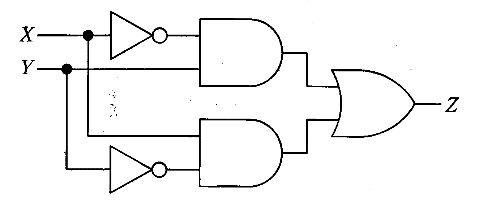
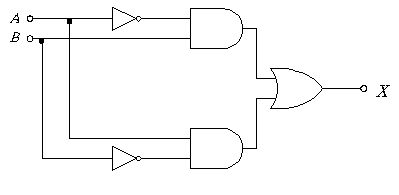
図の出力Xはどれか。
1
$\overline {A}\cdot \overline {B}+A\cdot B $
2
$\overline {A}\cdot\ B+A\cdot\ \overline {B}$
3
$\left( A+B\right) \cdot \left( A+\overline {B}\right) $
4
$\left( A+B\right) \cdot \left( A+\overline {B}\right) $
5
$\overline {A}\cdot \left( A+B\right) +B\cdot \left( \overline {A}\cdot \overline {B}\right) $
55
臨床工学技士国家試験 -
第37回 午後
類似度 75.9%
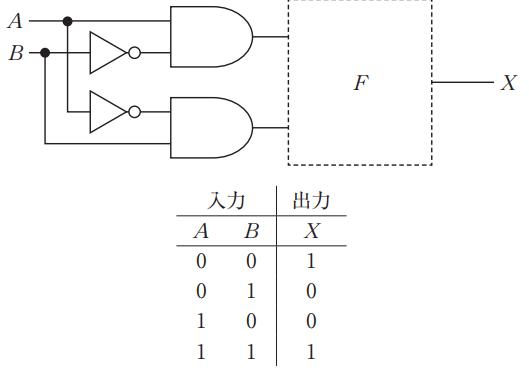
図の回路と等価な論理式はどれか。
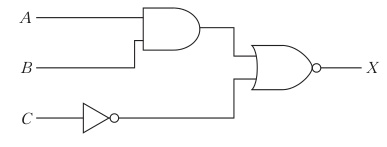
1
$X = A \cdot B + C$
2
$X = A \cdot B + \overline{C}$
3
$X = (\overline{A} + \overline{B}) \cdot C$
4
$X = (A + B) \cdot C$
5
$X = (A + B) \cdot \overline{C}$
広告
広告
31
臨床工学技士国家試験 -
第8回 午後
類似度 71.3%
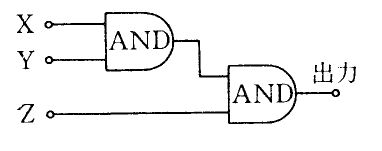
図に示す論理回路について正しいのはどれか。
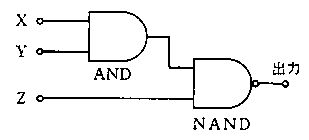
a
入力Xが1のとき、出力は常に1である。
b
入力Xが0のとき、出力は常に0である。
c
入力Zが1のとき、出力は常に0である。
d
入力Zが0のとき、出力は常に1である。
e
入力X、Y、Zがすべて1のとき、出力は0である。
組み合わせ:
1. a b
2. a e
3. b c
4. c d
5. d e
20
臨床工学技士国家試験 -
第17回 午後
類似度 69.7%
図の出力として正しいのはどれか。
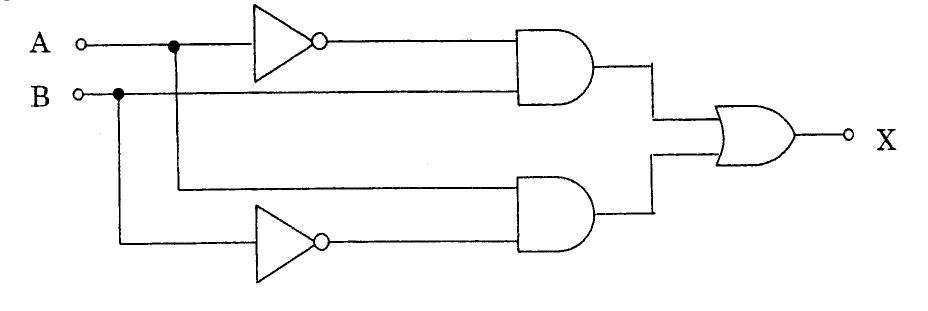
1
$X=\overline {A}\cdot \overline {B}+A\cdot B$
2
$X=\overline {A}\cdot B+A\cdot \overline {B}$
3
$X=\left( A+B\right) \cdot \left( A+\overline {B}\right) $
4
$X=\left( \overline {A}+B\right) \cdot \left( A+\overline {B}\right)$
5
$X=\overline {A}\cdot \left( A+B\right) +B\left( \overline {A}+\overline {B}\right)$
広告